「原理から学ぶ高校物理」 第１講 §1 粒子の運動の表現, 位置・速度・加速度

基本演習はこちらからダウンロードしてください

基本演習§1.pdf

23.8 KB

ファイルダウンロードについて

ダウンロード

■力学の目標

まず力学の勉強を始める前にその目標を押さえておきましょう。力学の目標は物体の「（未知の）運動がわかること」です。簡単に言ってしまえば物体が「いつ」、「どこ」にいるかを知ることができればいいわけです。そして「いつ」、「どこ」を物理では「時刻」、「位置」と呼びます。そしてこれらを客観的に表現するために数学を道具として使います。これから位置と時刻を数学を用いて表現したいと思います。

（ⅰ）位置

位置は数学でもおなじみではあるかと思いますが、(３次元)座標を用いて表します。たとえば空間上で物体の位置を指定する時は図のように空間上に３つ軸（$${x,y,z}$$軸）をとってあげます。

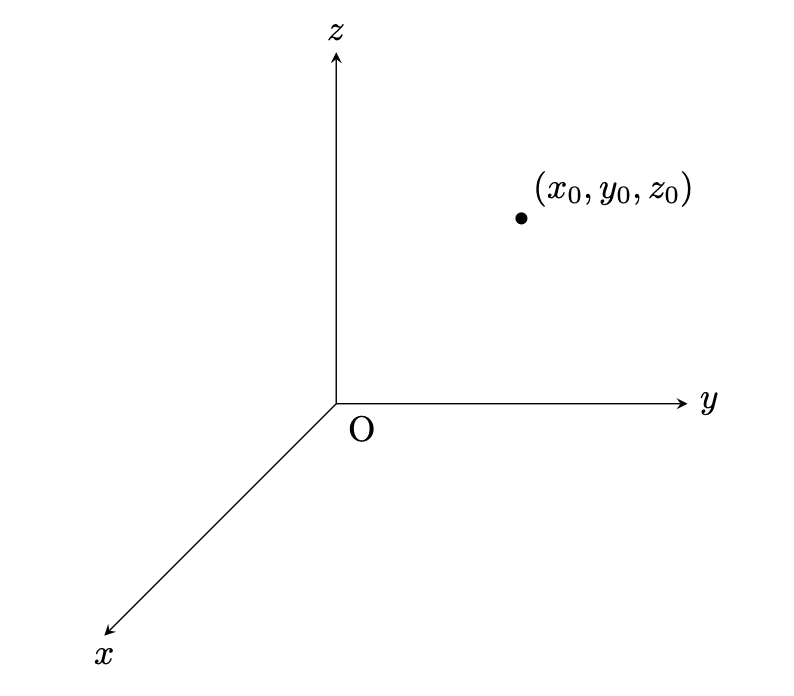
(注１)軸と原点の取り方は自由です。(問題で指定されていなければ) ただし右手系で取るのが一般的です。

(ⅱ)時刻

みなさんは時間を測る時に何を使いますか？たぶんストップウォッチを使いますよね。ストップウォッチって自分が最初に押したタイミングが基準になって過去から未来に数が増えていきますよね。このように時刻は原点(基準)を自由にとって実数$${t}$$に対応づけてあげます。また時刻$${t}$$の向きは過去から未来を正としてあげます。

(ⅰ)(ii)を踏まえれば(未知の)運動がわかるとは、すべての時刻$${t}$$での（位置の）座標がわかることになります。すなわち物体の位置ベクトルを$${\vec{r}}$$とすれば
位置が$${\vec{r}(t)=\begin{pmatrix} x(t) \\ y(t) \\ z(t) \end{pmatrix}}$$のように時刻tの関数として求められればいいわけです。
(例)
$${\vec{r}(t)=\begin{pmatrix} 2 \\ t \\2t-1\end{pmatrix}}$$
と求まったとします。この$${t}$$に実数を代入すれば位置がわかりますよね。

■微分・積分

前回、お話しした通り力学では物体の位置が$${\vec{r}(t)=\begin{pmatrix} x(t) \\ y(t) \\ z(t) \end{pmatrix}}$$のように時刻tの関数として求められればよかったわけです。議論を簡単にするためにとりあえず１次元での運動にについて考えたいと思います。すなわち$${x=x(t)}$$を考えます。したがって、今回は$${x(t)}$$を求めることができればいいわけです。それを求めるための道具として微分積分を学んでいきます。

(i)微分

例えば、空を飛んでいるをキャッチしたくて、ボールの軌道を予測したかったとします。(想像してもらうのは現実の3次元でいいのですが、ボールの軌道が１次元運動であるとします笑)みなさんならどうやって予測しますか？多くの人は、ある一瞬の間でのボールの動きを見て、ボールが飛んでくる位置を予測しますよね？なのでこの未知の$${x(t)}$$を求めるとして、ある時刻$${t}$$で未知$${x-t}$$グラフの曲線を一瞬の時間$${\Delta t}$$で分解してみます。そうすると図のように曲線を切り取ることができます。($${\Delta t}$$の間での$${x}$$の変化を$${\Delta x}$$とします。)

これを議論するために数式に持ち込みたいのですが、うねうねしてるのでちょっと厳しそう。ただこの部分的な曲線がもし直線であれば、その直線の傾きがわかれば数式化できそうですね。ここで昔の人は思いました。$${\Delta t,\Delta x}$$がめちゃくちゃ小さければ曲線を直線にみなせるんじゃないかと。(たしかに地球って丸いのに僕たちは丸みを感じることってすくないですよね。むしろ平坦だと思いますよね。)では$${\Delta t,\Delta x}$$が十分小さいとき$${x=x(t)}$$を直線とみなせるとします。また、この時の$${\Delta t,\Delta x}$$を$${dt,dx}$$と書きます。

そうするとこの線分の傾きを$${x'(t)}$$とすれば$${dx=x'(t)dt}$$と表せます。これを$${x=x(t)}$$の微分と呼びます。これを各点で集めれば$${x(t)}$$も表せそうな気がします。

(補足)また、$${x(t)}$$がわかっている時、$${x'(t)=\frac{dx(t)}{dt}}$$を各点について$${x(t)}$$から求める操作を微分すると呼びます。計算方法は

$$
\frac{dx}{dt}=\lim_{\Delta \to \infty} \frac{\Delta x}{\Delta t }=\lim_{\Delta t\to \infty} \frac{x(t+\Delta t)-x(t)}{\Delta t }
$$

から計算できる。

(ⅱ)積分

分割した微小な線分$${dx(=x'(t)dt)}$$を集め直し$${x(t)}$$を作る操作を積分と呼びます。そしたら$${(t_0,x_0)→(t_1,x_1)}$$における$${dx(=x'(t)dt)}$$を集めてみよう

$$
\begin{align*}
&\int _{x=x_0}^{x=x_1}dx\\
=&\int _{t=t_0}^{t=t_1}x'(t)dt \\
=&x(t_1)-x(t_0)\quad (=\, x_1-x_0)
\end{align*}
$$

まだ$${x(t)}$$ は求まってない。ここで$${x=x_1}$$は任意なので$${x_1\rightarrow x}$$とすれば

$$
\begin{align*}
x(t)-x(t_0)=\int _{t=t_0}^{t=t_1}x'(t)dt \\
\Leftrightarrow x(t)=x(t_0)+\int _{t=t_0}^{t=t_1}x'(t)dt
\end{align*}
$$

となり、$${x(t_0)}$$と$${x'(t)}$$がわかっていれば未知の$${x(t)}$$を求めることができます！簡単に言ってしまえば積分というのは複雑な未知量を単純な既知量から求めるためにあるものです。

■位置・速度・加速度

位置$${x(t)}$$を求める道具として微積分を学びました。今回は$${x(t)}$$を求めていきたいと思います。前回、$${x(t)}$$を求めるためにその$${x'(t)}$$が必要であることがわかったわけです。そしてこれを

$$
v(t)\stackrel{\mathrm{def}}{=}\frac{dx(t)}{dt}(=x'(t))　　(\because dx=x'(t)dt)
$$

と定め、これを速度と呼びます。

そしてまたこの速度$${v(t)}$$を知るためには$${v'(t)}$$
が必要になります。これを

$$
a(t)\stackrel{\mathrm{def}}{=}\frac{dv(t)}{dt}(=v'(t)=x''(t))　　(\because dv=v'(t)dt)
$$

と定め、これを加速度と呼びます。

そしてまたこのそしてまたこの加速度$${a(t)}$$を知るためにはその時間微分$${a'(t)}$$が必要になり…
と無限に微分することになる。実は加速度$${a(t)}$$は全く別の方法で求められることがわかっている。その方法については後でお話しするとして、とりあえず$${a(t)}$$がわかっているとして$${x(t)}$$を求められるようになろう！

$${x(t)}$$を細かく分割した$${dx=v(t)dt(=x'(t)dt)}$$を集めると位置$${x(t)}$$になります。これと同様に$${v(t)}$$を細かく分割した$${dv=a(t)dt(=v'(t)dt)}$$を集めると速度$${v(t)}$$になります。実際に$${t=t_0\rightarrow t=t(任意)}$$まで集めてみると

$$
\begin{align*}
v(t)&=v(t_0)+\int _{t=t_0}^{t=t}dv\\
&=v(t_0)+\int _{t=t_0}^{t=t}a(t)dt
\end{align*}
$$

となる。
次にx(t)の微分を集めてあげると

$$
\begin{align*}
x(t)&=x(t_0)+\int _{t=t_0}^{t=t}dx\\
&=x(t_0)+\int _{t=t_0}^{t=t}v(t)dt\\
&=x(t_0)+\int _{t=t_0}^{t=t}\{v(t_0)+\int _{t=t_0}^{t=t}a(t)dt\}dt\\
&=x(t_0)+v(t_0)(t-t_0)+\int _{t=t_0}^{t=t}(\int _{t=t_0}^{t=t}a(t)dt)dt\\
\end{align*}
$$

となり確かに加速度$${{a(t)}}$$から位置$${x(t)}$$は求まる。一応$${v(t_{0}) ,x(t_{0})}$$も必要であり、$${v(t_{0}) ,x(t_{0})}$$の情報を初期条件と呼ぶ。

（練習問題） 

加速度$${a(t)=\alpha}$$、初期条件$${v(0)=v_0, x(0)=x_0}$$が与えられている時$${v(t),x(t)}$$を求めよ。

（解答）

$$
\begin{align*}
v(t)&=v(0)+\int_0 ^t a(t)dt \\
&=v_0+\int_0^t \alpha dt \\
&=v_0+\alpha t\\ \\
x(t)&=x(0)+\int_0^tv(t)dt \\
&=x_0+\int_0^t (v_0 +\alpha t)dt \\
&=x_0+v_0 t +\frac{1}{2}\alpha t^2
\end{align*}
$$

それでは基本演習1-1,1-2を解いてみましょう。

1-1

まず速度の定義は$${v(t)=\frac{dx}{dt}}$$ですよね。今回$${x(t)}$$がわかっているので定義から計算することができます。

$$
\begin{align*}
&(1)v=\frac{d}{dt}(2)=0\\
&(2)v=\frac{d}{dt}(2t+1)=2\\
&(3)v=\frac{d}{dt}(4t^2+3t+1)=8t+3\\
&(4)v=\frac{d}{dt}(2\sin {t}+\cos {3t}+1)=2\cos {3t}-3\sin{3t}\\
&(5)v=\frac{d}{dt}(3e^{2x}+3)=6e^{2x}
\end{align*}
$$

1-2

■位置・速度・加速度の練習問題の類題です。

$$
\begin{align*}
(1)\ v(t)&=v(0)+\int_0 ^t a(t)dt \\
&=-2+\int_0^t 4 dt \\
&=-2+4 t\\ \\
x(t)&=x(0)+\int_0^tv(t)dt \\
&=1+\int_0^t (-2 +4 t)dt \\
&=1-2 t +2 t^2\\\\
(2)\ v(t)&=v(0)+\int_0 ^t a(t)dt \\
&=3+\int_0^t 0 dt \\
&=3\\ \\
x(t)&=x(0)+\int_0^tv(t)dt \\
&=5+\int_0^t 3dt \\
&=5+\frac{3}{2} t^2\\\\
(3)\ v(t)&=v(0)+\int_0 ^t a(t)dt \\
&=3+\int_0^t (2t+1) dt \\
&=3+t^2+t\\ \\
x(t)&=x(0)+\int_0^tv(t)dt \\
&=1+\int_0^t (3+t+t^2)dt \\
&=1+3t+\frac{1}{2}t^2+\frac{1}{3}t^3
\end{align*}
$$

■速度・速さ

前回、速度を以下のように定義しました。

$$
v(t)=\frac{dx}{dt}
$$

ここで速度$${\frac{dx}{dt}>0}$$のとき、$${t}$$は過去から未来を正の向きにとるので$${dt}$$はどんなときでも正になるので$${dx>0}$$。したがってその微小時間$${dt}$$で物体は$${x}$$軸正方向に動きます。

また速度$${\frac{dx}{dt},0}$$のとき、$${dt}$$はどんな時でも正になるので$${dx>0}$$。したがってその微小時間$${dt}$$で物体は$${x}$$軸負方向に動きます。

速度$${\frac{dx}{dt}}$$のように大きさと向きを持つ量をベクトル量と呼ぶ。
一方、速度の大きさ$${|\frac{dx}{dt}|}$$を速さと呼び、大きさのみを持つ量をスカラー量と呼び、ベクトル量と区別します。

1-3

(1) 物体の加速度が聞かれている。今回$${v-t}$$グラフ、すなわち$${v(t)}$$が与えられている。したがって、$${v(t)}$$をグラフから読み取り、加速度の定義$${a(t)=\frac{dx}{dt}}$$から加速度を計算すれば良い。

$$
v(t)=
\begin{align*}
\begin{cases}
2t\quad &(0≤t≤1)\\
2\quad &(1≤t≤2)\\
-2t+6\quad &(2≤t≤4)\\ 
t-6\quad &(4≤t≤6)\\
\end{cases}
\end{align*}
$$

したがって加速度の定義から

$$
a(t)=
\begin{align*}
\begin{cases}
2\quad &(0≤t≤1)\\
0\quad &(1≤t≤2)\\
-2\quad &(2≤t≤4)\\ 
1\quad &(4≤t≤6)\\
\end{cases}
\end{align*}
$$

したがって加速度のグラフは

(別解)

■微分積分　で学んだように、一般に$${y=f(x)}$$で$${f'(x)=\frac{df(x)}{dx}}$$は$${y-x}$$グラフの各地点での曲線の傾きを表す。これと同様に$${a(t)=v'(t)=\frac{dv(t)}{dt}}$$は$${v-t}$$グラフの曲線の各$${t}$$での傾きになります。したがって与えられた$${v-t}$$グラフの曲線の傾きを読み取れば、ただちに加速度$${a(t)}$$は求まります。別解として紹介しましたが速度の$${t}$$の関数を求める必要がなくなるので、こちらの方がスピードが早いです。

(2) 位置$${x(6)}$$を求めたい。いつも通り加速度を2回積分して位置を求めたいところだが、今回はその１回積分した先である速度$${v(t)}$$が与えられているのでわざわざ2回積分する必要がない。また初期条件が必要だが、問題文より$${t=0}$$のとき$${x=0}$$とあり$${x(0)=0}$$と得られる。これで$${v(t),x(0)}$$がわかったので積分して$${x(6)}$$を求めてあげればよい。

$$
\begin{align*}
x(t)&=x(0)+\int_0^tv(t)dt \\
&=0+\int_0^1 2t dt+\int_1^2 2dt+\int_2^4 (-2t +6) dt+\int_4^6 (t-6) dt\\
&=1
\end{align*}
$$

と求まる。これでできるけど計算クソめんどくさいね。もっといい方法がないか考えてみたいと思います。

■グラフの解釈まとめ

$$
x(t)=x(t_0)+\int _{t_0}^{t}v(t)dt
$$

から位置$${x(t)}$$を計算したが$${\int _{t_0}^{t}v(t)dt}$$が$${v-t}$$グラフ上で何を意味するか考えます。
まず、$${v(t)dt}$$を図示すると、

となり、$${v(t)dt}$$はこの長方形の面積$${dS}$$を表す。また$${\int _{t_0}^{t}v(t)dt}$$の$${\int _{t_0}^{t}}$$は「$${t=t_0}$$から$${t=t}$$まで足し合わせる」という意味。これを図示すると

したがって、$${\int _{t_0}^{t}v(t)dt}$$は$${v-t}$$グラフの赤で囲まれた部分の面積となる。

(注1)
$${v(t)<0}$$の場合、微小面積$${dS=v(t)dt<0}$$となり、
面積が負になることがあります。(符号付き面積）
この符号付き面積の物理的意味についてはこの後の(注2)でお話しします。

それでは前回の1-3(2)を再考してみましょう。

$${\int _{t_0}^{t}v(t)dt}$$は$${v-t}$$グラフの面積になり、$${0≤t≤3}$$では$${v(t)≥0}$$なので面積は正、$${3≤t≤6}$$では$${v(t)<0}$$なので面積は負になります。

$$
\begin{align*}
x(6)&=x(0)+\int _0^6 v(t)dt
&=0+\frac{1}{2}\cdot (1+3)\cdot 2+\frac{1}{2}\cdot 3 \cdot (-2)
&=1
\end{align*}
$$

となり前回と同じ答えになりました。

まとめ

一般に$${y=f(t)}$$で$${f'(t)=\frac{df(t)}{dt}}$$は$${y-t}$$グラフの曲線の各$${t}$$での傾きを表します。また、$${\int_{t_0}^xf'(t)dt}$$は$${\int_{t_0}^tf'(t)dt = f(t)-f(t_0)}$$から1回積分した量の$${t=t_0}$$から$${t=t}$$の変化を表します。

これらを元に$${x-t,v-t,a-t}$$グラフの解釈をそれぞれまとめます。

(ⅰ)$${x-t}$$グラフ

傾き→速度$${v(t)=\frac{dx(t)}{dt}}$$
面積は物理的な意味はないので使いません。

(ⅱ)$${v-t}$$グラフ

傾き→加速度$${a(t)=\frac{dv(t)}{dt}}$$
面積は位置の差すなわち位置の変化を表し、これを変位と呼びます。

(注2)
$${\int _{t_0}^{t}v(t)dt}$$は符号付き面積で、この符号の物理的な意味について考えます。$${\int _{t_0}^{t}v(t)dt}$$は上でも述べたように、変位を表すわけです。したがって$${\int _{t_0}^{t}v(t)dt>0}$$である場合は変位が正、すなわち$${t=t_0 \text{から}t=t}$$の間に位置$${x}$$が大きくなったことを表します。逆に$${\int _{t_0}^{t}v(t)dt<0}$$である場合は変位が負、すなわち$${t=t_0}$$から $${t=t}$$の間に位置$${x}$$が小さくなったことを表します。

(Ⅲ)$${a-t}$$グラフ

傾きは特に物理的な意味はありません。
面積は速度の差すなわち速度の変化を表し、特に呼び名はありませんが速度変化と呼ぶことが多いです。

(ⅰ)~(Ⅲ)を比較すると(ⅱ)が一番情報量が多いので$${v-t}$$グラフを書くのが便利そう。ただ下図のような$${v-t}$$グラフの曲線がくねくねしてると面積を求めるのに結局積分が必要になってしまうので、面積を三角形、台形の面積公式から求められるような、1-3のような等加速度運動の場合は$${v-t}$$グラフを描くと解きやすくなります。

また今回のセクションの確認問題は以下からダウンロードしてください。

確認問題§1.pdf

56.8 KB

ファイルダウンロードについて

ダウンロード

記事はこれで以上となります。
ご意見、ご要望等ございましたら、noteの「クリエイターへのお問い合わせ」からよろしくお願いします。

「クリエイターへのお問い合わせ」

お問い合わせ | note（ノート）