工学生の雑語り 身長と正規分布

導入

先日、大学で体力測定があった。

体力測定では、BMIや体脂肪率なども測定するのだが、大まかに身長が階級分けされて、自分の身長に近いところに並び、順番を待って測定を行うことになっていた。

自分の列にはあまり人が並んでおらず、直ぐに計測が終わったのだが、一緒に回っていた友達のいた列はかなり長く、結構な時間待たされていた。

そこで、身長分けの方法をよく見ると、なんと「身長を4cmごとに区切って、各グループに2台の測定器が置いてあるだけ」だった。

「平均の身長付近の台数増やせよ！正規分布知ってるかぁ！？」とか思ったんで、今回は、このケースの最適解を探りつつ、正規分布の復習をしていきます。

正規分布とは

まず、正規分布について軽く説明すると、

平均値=中央値=最頻値

となるような、確率分布のことで、身長も＂だいたい＂正規分布に従うとされています。(今回は身長は正規分布だとして考えています)

グラフはこんな感じ

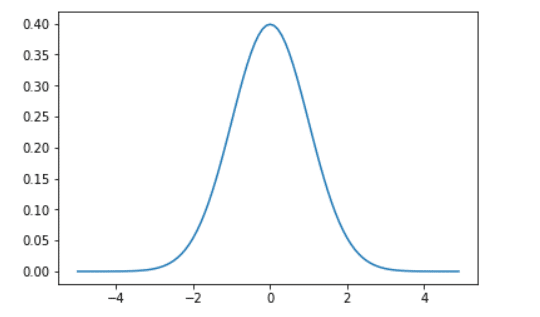
横軸が確率変数(ある事柄に割り当てられた値をとる変数)、縦軸は確率密度を示し、積分する事である区間の確率変数に対する確率が求まります。

正規分布の場合、確率変数が中央に近いほど確率密度が大きい値をとり、離れれば離れるほど小さい値をとります。

例えば、確率変数をXとした時、-1<X<1と、2<X<3で積分をすると前者の方が値が大きい、すなわち前者の起こる確率の方が高いことが分かります。

正規分布は確率変数Xを操作することで、標準正規分布という扱いやすい分布に変えることが出来ることが知られており、

平均μ、分散σ^2の正規分布があった場合(確率変数XがN(μ,σ^2)に従う)

Z=X－μ/σ

Xはこのように線形変換します。この時、Zの平均は0、分散は1になります。(この操作は正規分布に関わらず行うことができ、平均0分散1になります)

標準正規分布には、標準正規分布表というものがあり、これを用いることで難しい計算なしで確率を求めることができます。

また、確率密度関数を

-∞<X<x

の範囲で積分したものを累積分布関数と呼び、縦軸は確率変数Xがx以下の値になる数（累積確率）を表します。

今回は、ある確率に対してのの x の値を知りたかったので、標準正規分布ではなくこちらを使って解いていきました。

問題設定

まず、今回のケースの状況を簡単化しつつ整理すると、

<データ>
測定器の台数 20台
大学生男子の身長平均 = 170cm
身長の標準偏差 = 5.5 ←(文科省のデータをもとに比較的綺麗な値にしました)

<やりたいこと>
「大学生男子を身長順でグループ分けし、各グループの人数を同じくらいにする」

すなわち、問題は

「確率変数XがN(170,5.5^2)に従うとき、

区間(Ai-1,Ai) (i=20)に対する確率が全て等しくなるような(Ai-1,Ai)を求めよ。」

になります。

具体例をもとに問題を考えると堅苦しい数式もきちんとした意図があることが読み取れて楽しいですね。

解答

ここまで長ったらしく言ってきましたが、やることはいたって簡単です。

身長データの累積分布関数の逆関数により、累積確率に対する確率変数（身長）を求める

です。

Excelには、これにピッタリな関数NORM.INV()が用意されており、平均と標準偏差、累計確率を与えると、それに対応する確率変数を求めてくれます。

ということで実行してみた結果がこちら

例えば、累計確率0.3の場合、下位30％には身長167.1158cm未満の人が入ることになります。

すなわち、大学生男子を身長順に20グループに分けたとき、各グループの人数をほぼ同じにするには、

0~160.9533
160.9533~162.9515
・
・
・
・
・
177.0485~179.0467
179.0467~

にすればいいということですね。

感想

完全に思い付きで始めたのですが、思いの他価値のある寄り道ができて面白かったです。（プログラミングでのplot、累積分布関数、Excel、etc…）

これを大学に送り付けてやろうかとも思いましたが、冷静になってみると習いたての知識を使いたい理系大学生感まるだしだったので、やめることにしました。

現実に即して数学していくのは好きなのでまた何かあったら書こうと思います。

P.S. 友達にこの話をしたところ、渋い顔をされました。反応の度合いも彼の渋い顔を平均とした正規分布になるんじゃないかな、と思った瞬間でした。