
高校物理における微積分
「高校物理に微積を使うべきか否か」
これは(大学受験における)物理業界を長年悩ませてきた問題の一つです。今回はこの問題について個人的な見解を書きたいと思います。
まずこの問題への自分なりのアンサーは「是非微積を使うべきである」です。そもそも微積分という学問(特に微分)は物理を定量的にやるために生まれた概念・方法であるため、
微積抜きで物理を勉強するのは野球のルールを知らずに野球をしているようなものなのです。
(ここでの「野球をする」は指示された通りに動いていればルールを知らずとも少なくともプレーはできると言う意味合いで使っています。)「言い過ぎだろ!」と思われる方もいらっしゃるかもしれませんが、自分ではまったく誇張だとは思っていません。むしろ適した表現だと思っています。ここから私がこのように考える理由を述べていきたいと思うのですが、その前にいくつか話しておきたいことがあるので、まずはその前提から話していきたいと思います。
1.議論が起こる理由
そもそもなぜ高校物理における微積の使用を巡って議論が起こるのでしょうか?これには大きく分けて2つほど理由があると思います。
まず1つめはカリキュラム的な理由です。高校数学で微積を初めて習うのは数学Ⅱです。普通の高校は数学Ⅰ、数学Aを終了した後に数学Ⅱを習うはずですので、微積を習い始めるのはおそらく2年生の時でしょう。そうすると物理基礎を習い始める方が微積を習うよりも先になってしまうということが起こりうると思います。すると、高校物理で一番始めに習う速度・加速度の定義を微積なしでしなければならなくなってしまいます。高校物理の力学で微積の対象になるのは速度・加速度(時間を変数とするもの)が非常に多いので、そのように定義した時点で今後の授業では微積をほとんど使えなくなってしまうのです。
もう1つの理由は難解さです。たとえば空気抵抗を含む落体運動中の物体の速度vₜは
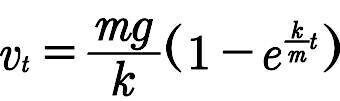
で与えられます。(m:質量、g:重力加速度、k:比例定数、e:ネイピア数、t:時刻)これを求めるには微分方程式の知識と数学Ⅲで習う積分法の知識を持っている必要があります。高校1,2年生で数学Ⅲを習っていない人がいきなりこの式の導出を教わっても理解できるはずがありません。このように物理基礎の中にも実は数学Ⅲレベルの内容は平気で含まれているのです。しかし、これを厳密に教える・教わるのは指導者にとっても生徒にとっても難解であることは言うまでもありません。(指導者は全員が話を理解できるように教えるはずですから。)ですから高校物理を微積を用いて教えるのは少数派となっています。
このように微積を使いたくても使えないケースがどうしても生じてしまうため、賛成派と反対派の間で微積の使用を巡って議論が起こるのです。
2.微積の使い方
高校物理で微積を使うとはどのような使い方を指すのでしょうか。これも2つに大別できます。1つは概念を教えるときに使う方法。もう1つは問題を解くときに使う方法です。順に見ていきましょう。
(1)概念説明における微積
こちらは問題を解くときではなく、新しい内容を教えるときに微積を使う方法です。たとえば物理基礎で一番始めに習う公式
![]()
は、加速度の定義より次のように導くことができます。
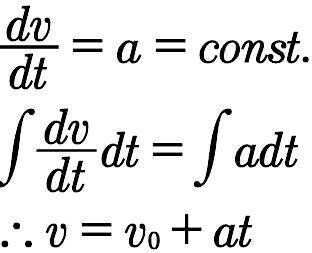
(const.は一定を表します。)(v₀は初期条件t=0のときv=v₀から得た積分定数です。)
また、仕事の定義として習う
![]()
は実はもう少し厳密に次のように定義されています。
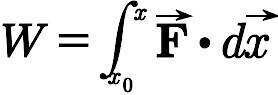
(x₀地点からx地点までの仕事と考えています。)(簡単のためにx方向のみで考えています。)
このように一般的に公式として教えられるものや定義がどのように成り立っているのかを説明する際に微積を用いる方法が「概念説明における微積」と私が呼んでいるものになります。
(2)解答における微積
こちらは実際に問題を解くときに微積を使う方法になります。こちらも具体例を通して見ていただきましょう。例題は東北大学2012前期の物理第1問の問(3)です。非常に良い問題ですので、答えを見る前に実際に手を動かして解いてみることをおすすめします。(問題は著作権の都合上載せていません。教学社の『東北大の物理15ヵ年』などを参照してください。)

こちらは私の解答・解説になります。(字が汚いのはご了承下さい……。)この問題の重要なポイントは「動摩擦係数が一定ではなく位置xによる変数である」というところです。つまり、先述の仕事の積分による定義を使わなければならないのです。(仕事は積分する変数が位置xであることを確認してください。)したがって、写真のように解くことができます。この問題はグラフが与えられているのでグラフの面積を求めることで積分せずに解くことはできます。しかし明らかにこのグラフは、積分で教わっていない人もいるだろうから……という″カリキュラム上の配慮″以外の何物でもありません。もしグラフが与えられていなければ積分で解く以外に方法はない気がします。このように、微積を用いて問題を解く方法が「解答における微積」と私が呼んでいるものになります。
以上、微積の2つの使い方について述べてきました。正直な話、(2)のように微積を使って問題を解くことはあまりありません。先程も触れましたが、大学側もカリキュラム的なことは配慮していますので、基本的に微積を使わないと絶対に解けない問題は出ません。(Δを用いてごまかしたり後期では平気で問うたりしますが……。)私が微積を使うべきだと考えているのはむしろ前者です。最初に「微積を是非使うべきだ」と言いましたが、それには″概念説明の際に″という条件を付け足さなくてはなりません。(もちろん微積でしか解けない場合は「解答における微積」を使ってくださいと言う他ありませんが。)長々と脱線してしまいましたが、次に微積で学ぶべき理由・メリットについて話していきます。
3.本題:微積で学ぶべき理由
微積を使うことのメリットはなんといっても「導出できるものが増えること」でしょう。初めに具体例として取り上げた空気抵抗ありの落体運動について、受験期にメモしていたものの写真があったのでそれをご覧いただきましょう。

これは微積抜きでは求めることができません。このように微積を使うと導くことができる事実が多くなるのです。
また微積を使うと「概念を統一的に見ることができる」というメリットもあります。ここでは例として運動量保存則と力積について取り上げてみたいと思います。運動方程式ma=FのFを外力のみとして考えることができるとき次の事実が得られます。
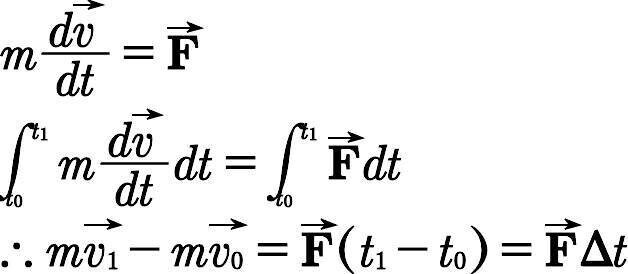
(t₀からt₁までの運動を考えています。)(v₁ベクトル,v₀ベクトルはそれぞれt=1,t=0のときの速度です。)
特に外力が加わっていない、すなわちF=0のとき、
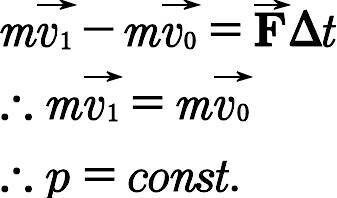
ということも言えます。(pは運動量です。)
この事実は
外力が加わるとき運動量の変化は力積と等しい。
外力が加わらないとき運動量は保存する。
ということを示しています。1つの物体のみで考えているため簡易的ではありますが、運動量保存則と運動量・力積の関係式を導くことができました。これも微積を用いたお陰でスムーズに、そして簡潔に求めることができています。多くの人が運動方程式と運動量保存を別個に考えているところ、微積を使うことで同じ見方で考えられるのです。どうですか、今まで別々に見ていたものが1つに繋がって、統一的に見えてきませんか?
これはメリットというよりもはや微積を使うべき理由そのものです。物理学というのは一般化の学問です。できる限り簡潔な法則で多くのことが説明できることを良しとする学問なのです。(古典力学ではニュートンの三大法則が、電磁気学ではマクスウェルの法則がこの役割を担っていますね。)ですから、微積を使って1つの理論・法則から演繹的に多種多様な事実が導けるのであれば、それこそが物理学の正しい在り方であるはずです。
野球のルールを知らなくても野球をすることはできます。しかし目的意識がなければ上達はしません。物理学も同じだと考えています。1つの法則から枝葉を広げて多種多様な事実を導くという物理学の目的を意識することで、時間がかかるように思えるかもしれませんが着実に力になると思います。
これが私が高校物理において微積分を使うべきだと考える理由になります。
4.諸注意
今まで微積の有用性について述べてきたわけですが、高校生が扱う際には注意しなければいけないこともあります。それは「どこまで踏み込んでもよいか」ということです。微積で物理を勉強していると、線積分などが出てくると思います。これをちゃんと数学的に厳密に勉強しようとすると大変な労力となります。もちろん厳密に勉強することは正しい態度であり、そうあるべきなのですが、いかんせん高校生には受験まで長くても3年しか時間がありません。他の勉強もしなければならないでしょう。そうすると、いわゆる「物理数学」に手こずっていては時間が足りなくなってしまいます。数学Ⅲレベルならまだしも大学数学で手こずってしまうのは微積推奨派の意図するところではありません。線積分などは簡単に意味だけを分かっておくだけで十分だと思います。そこら辺の塩梅は是非参考書に頼りましょう。参考書に掲載されているレベルまでは踏み込んでも大丈夫です。
5.参考書
微積を用いている物理の参考書を紹介します。
(1)『新・物理入門』著:山本義隆 (駿台文庫)
微積を用いた物理でお馴染みの参考書です。入門とあるのに全然簡単ではないその内容は受験業界では語り草となっています。ネタにされやすい本書ですが内容は大変良いです。教科書、某用問題集レベルができるようになったら読んでみるべきだと思います。ただし、レベルは非常に高いので数学Ⅲが分かるようになってから読むのが良いと思います。自分は運動量保存、力学的エネルギー、仕事の辺りに大変感動し、何度も読み返しました。名著です。
(2)『理論物理への道標(上・下)』著:杉山忠男 (河合出版)
この本に関してはまだ読んだことがないためなんとも言えませんが、微積を用いた物理の参考書はこれと『新・物理入門』くらいしかないので挙げました。読んだらこの部分を加筆したいと思います。
(3)『学問としての高校物理(上・下)』著:吉田弘幸 (日本評論社)
これは私が初めて読んだときに衝撃を受けた本です。どちらかというと一般向けに近い気もしますが、微積を用いているので挙げました。この本は『新・物理入門』はちょっとレベルが高くて読めない、という人でも分かるくらいに丁寧に書かれています。入試問題でよくある設定を問題としてではなく例として取り上げ、そのときに成り立つ事実を微積を用いて導いています。微積で勉強するのが初めてという方におすすめする本としては、自分の中の現状のベストはこの本です。少々値が張るので、図書館などで探して借りてみるのも手だと思います。
最後までお読みいただきありがとうございました。
この記事が気に入ったらサポートをしてみませんか?
