
中学受験算数「場合の数」
1⃣樹形図で考える。
◯✕を4個並べるとき、○○が続かない並べ方は、何通りあるか。

左の図は、画面が切れていますが、左端は、◯です。
このように、左はしが〇と✕の、2通りの樹形図を描きます。
左の樹形図は、左から○○が二回続いているので、◯以降書かなくても良いです。
右の樹形図は、○○が続いている場所を消しましょう。
二つの樹形図で、最後の右列で残っているものを数えましょう。
3通り+5通り=8通り
< 解答 > 8通り
2⃣ごばんの目で考える
問1 AからBまで行くのに、何通りあるか。
ごばんの目の左側と右側は、すべて1通りです。
小さい四角の中をななめに対角線上に足していくと、四角形の右上の数字になります。
これで、あっという間に70が出ます。
< 解答 > 70通り
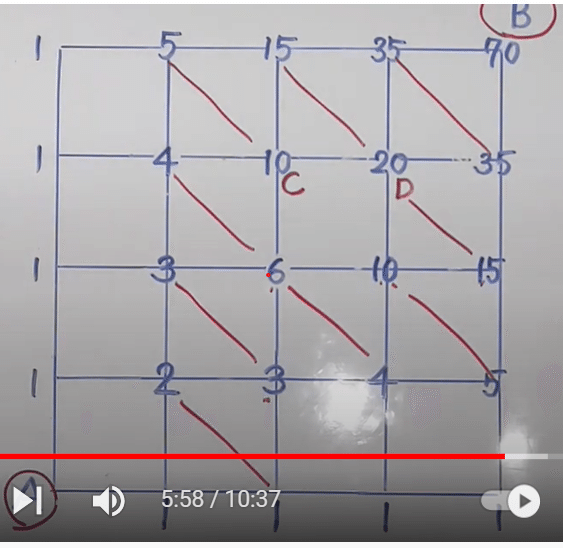
問2 CDを通らずに行く方法は、何通りか。
A~Cまで10通り。
D~Bまでは、DにAの位置が来たと考えてください。だから2通り。
10×2=20(CD)を通っていく
70-20=50通り
< 解答 > 50通り
