代数学の基本定理のシンプル（？）な証明

$${\underline{代数学の基本定理}}$$
$${n}$$を正の整数、$${f(z)=a_nz^n+a_{n-1}z^{n-1}+a_{n-2}z^{n-2}+\cdots +a_1z+a_0}$$（$${a_n,a_{n-1},a_{n-2},\cdots ,a_1,a_0}$$は複素数の定数で$${a_n \neq 0}$$）に対し、$${f(\alpha)=0}$$となる複素数$${\alpha}$$が存在する。

代数学の基本定理の証明は色々知られていますが、最近、ある本でシンプル（？）な証明を知りました。ただし、この本に書かれている通りに忠実に読むと誤っている部分がある（ように思う）ので、この本の証明を修正したものを紹介したいと思います。高校数学＋αで証明できます。高校数学範囲外で登場するものは「$${xy}$$平面上の有界閉集合$${D}$$上の連続関数$${w=f(x,y)}$$は、最大値と最小値を持つ」くらいです（「閉区間$${I}$$上の連続関数$${y=f(x)}$$は、最大値と最小値を持つ」の拡張版）。
出来るだけ分かりやすく解説しますので、ぜひ最後まで読んでください。

$${\underline{補題1}}$$
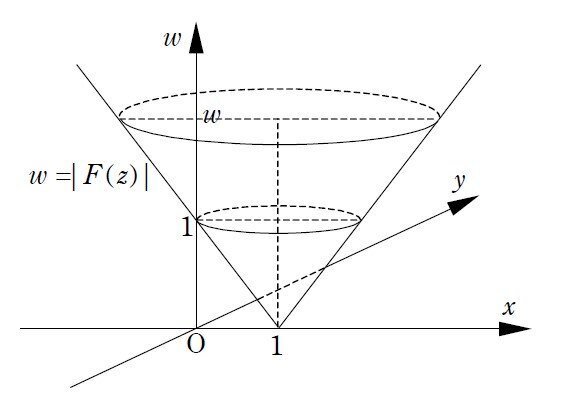
$${z}$$が全ての複素数を動くとき、関数$${w=|f(z)|}$$は最小値を持つ。

関数$${w=|f(z)|}$$は複素数平面（$${xy}$$平面）から0以上の実数を対応させる関数であり、そのグラフは$${xyw}$$空間における曲面となります。例えば、$${f(z)=z-1}$$のときは、関数$${w=|f(z)|}$$のグラフ（曲面）は次図のような円錐面（の半分）です（$${w=}$$一定（$${\geqq 0}$$）なる平面でこの曲面を切断すると、この平面上で中心$${1}$$、半径$${w}$$の円になるので）。

xyw空間内の曲面w=|z-1|

[補題1の証明]
$${z\neq 0}$$のとき
　　$${|f(z)|=|z|^n \left| a_n+\dfrac{a_{n-1}}{z}+\dfrac{a_{n-2}}{z^2}+\cdots +\dfrac{a_1}{z^{n-1}}+\dfrac{a_0}{z^{n}}\right|}$$
より、どのような$${0}$$以上の実数$${M}$$に対しても、適切な$${R>0}$$があり、「$${|z|>R}$$のとき必ず$${|f(z)|>M}$$」となる（つまり$${|z| \to \infty}$$のとき$${|f(z)| \to \infty}$$）。
$${M=|f(0)|}$$とし、このときの$${R}$$に対して$${D=\{ z~\big|~ |z| \leqq R \}}$$とすると、$${|f(z)|~(z \in D)}$$は最小値を持つ（∵$${D}$$は有界閉集合、$${w=|f(z)|}$$は連続関数）。これを与える$${z}$$を$${\alpha}$$とおく。また、$${z \notin D}$$のときは$${|f(z)|>|f(0)| \geqq |f(\alpha)| }$$。よって、この$${\alpha}$$は「$${z}$$が全ての複素数を動いたときの$${|f(z)|}$$の最小値」を与える。//

上記の最小値$${|f(\alpha)|}$$が$${0}$$であることを示しましょう。これが示されれば、$${f(\alpha)=0}$$となるので、代数学の基本定理が証明できます。

$${|f(z)|}$$を「$${-\alpha}$$だけ平行移動」した$${|f(z+\alpha)|}$$を考えると、これは$${z=0}$$で最小値を取ります。そこで、$${f(z+\alpha)}$$を改めて$${f(z)}$$とおきます。示すべきは$${|f(0)|=0}$$ですね。

$${\underline{補題2}}$$
複素数係数の多項式$${F(z)}$$に対し、$${F(z)}$$の係数をすべて共役に取り換えたものを$${\overline{F}(z)}$$とする。$${g(z)=f(z)\overline{f}(z)}$$とおく。
　(1) $${g(z)}$$は実数係数の多項式である。
　(2) $${|g(z)|}$$は$${z=0}$$で最小値を取る。

この補題により、以下では$${f(z)}$$の係数が実数のときを考えればよい、ということが分かります（補題2の証明の後に説明します）。

[補題2の証明]
(1) $${g(z)}$$の定義よりこれは多項式で、かつ$${\overline{g}(z)=\bar{f}(z)\overline{\overline{f}}(z)=\overline{f}(z)f(z)=g(z)}$$より、$${g(z)}$$の係数はすべて実数である。//
(2) $${|g(z)|=|f(z)||\overline{f}(z)|=|f(z)||f(\overline{z})|}$$である。$${|f(z)|,|f(\overline{z})|}$$はともに$${z=0}$$で（$${0}$$以上の）最小値を取るので、$${|g(z)|}$$も$${z=0}$$で最小値を取る。//

さて、$${|g(z)|}$$の最小値$${|g(0)|}$$が$${0}$$であることを証明します。これが示されれば、$${|f(0)||f(\overline{0})|=0}$$つまり$${|f(0)|=0}$$が得られます。この$${g(z)}$$を改めて$${f(z)}$$と置きます。このときの$${f(z)}$$の各係数$${a_n,a_{n-1},a_{n-2},\cdots,a_1,a_0}$$はすべて実数ですね。

さあ、あと少しです。もう少し頑張りましょう！

仮に$${|f(z)|}$$の最小値$${|f(0)|(=|a_n|)}$$が$${0}$$でない、つまり$${a_n \neq 0}$$とします。$${a_n<0}$$のときは$${-f(z)}$$を改めて$${f(z)}$$とおくことで、$${a_n>0}$$のときを考えれば良いですね。$${f(z)}$$を昇べきの順に書いて、$${a_n}$$の次に現れる項を$${a_m x^m}$$（$${a_m \neq 0}$$）とします。すると、
　$${f(z)=a_n+a_mz^m+z^{m+1}h(z)}$$（$${h(z)}$$はある多項式）
と書けます。

このあとの大雑把な流れは次の通りです。
「$${z}$$の絶対値を十分小さく取り、向きを適切に取れば（$${z}$$の$${m+1}$$次以上の項は微小なので無視して）$${f(z)\approx a_n-|a_m||z|^m}$$とすることができ、これの絶対値は$${a_n}$$よりも小さいので、$${|f(0)|=a_n}$$の最小性に矛盾する」
このことをきちんと示すと、次の通りです。

$${|z| \leqq 1}$$のとき$${|h(z)|}$$は有界、つまりある正の定数$${M}$$に対して$${|h(z)| \leqq M}$$となります（∵円板$${|z| \leqq 1}$$は有界閉集合、$${|h(z)|}$$は連続関数）。以下、$${z}$$をうまく取ることで $${|f(z)| < a_n}$$となることを示しましょう。

(i) $${\underline{a_m>0のとき}}$$
$${z=\varepsilon\exp\left( \dfrac{\pi i}{m} \right)}$$（$${0<\varepsilon<1}$$、$${i}$$は虚数単位）とおくと、（$${\exp\left( \dfrac{\pi i}{m} \right)=\cos\left( \dfrac{\pi}{m} \right)+i\sin\left( \dfrac{\pi}{m} \right)}$$ が「$${m}$$乗すると$${-1}$$となる数」であることに注意して）
　　$${f(z)=a_n-a_m\varepsilon^m+z^{m+1}h(z)}$$
なので、三角不等式（複素数$${Z,W}$$に対して$${|Z+W| \leqq |Z|+|W|}$$）を用いて
　$${|f(z)|\leqq |a_n-a_m\varepsilon^m|+|z^{m+1}h(z)|\leqq|a_n-a_m\varepsilon^m|+\varepsilon^{m+1}M}$$
となります。$${\varepsilon}$$を
　$${a_n-a_m\varepsilon^m>0}$$かつ$${-a_m\varepsilon^m+\varepsilon^{m+1}M<0}$$
　（つまり$${\varepsilon <\left(\dfrac{a_n}{a_m}\right)^{\frac{1}{m}}}$$かつ$${\varepsilon <\dfrac{a_m}{M}}$$）
を満たすようにとると、
　$${|f(z)|\leqq a_n-a_m\varepsilon^m+\varepsilon^{m+1}M < a_n}$$
です。これは、$${|f(z)|}$$の最小値が$${|f(0)|=a_n}$$であることに反し矛盾します。

(ii) $${\underline{a_m<0のとき}}$$
$${z=\varepsilon}$$（$${0<\varepsilon<1}$$）とおくと、
　　$${f(z)=a_n-|a_m|\varepsilon^m+z^{m+1}h(z)}$$
となります。あとは、(i)と同様に考えれば矛盾が生じます。

よって、$${|f(0)|=0}$$が得られる、というわけです。

以上より、代数学の基本定理が証明されました。//