【ABC353】AtCoder ABC353 Problem Cを解き直す

平目＠インフラエンジニア

AtCoder Beginning Contest 353、参加して来ました。

AB問題の2完で今回は挫折。C問題のTLEが解消出来ず、解き切れなかった…という事で、多少日にちは経ちましたが、悔しい想いを解消する為にも、コンテスト後に解き直した軌跡を記していきます。


AtCoder ABC353 problem C

問題内容は以下からご確認下さい。

提出1回目(コンテスト内)

配列内から２つを取り出した組み合わせの和を$${10^8}$$で割った余りの値を$${f(x+y)}$$とした時、その全ての組み合わせでの$${f(x+y)}$$の総和を求める物です。

まあ愚直な計算では計算量的に解けないだろうな、と分かってはいたものの、ひとまず非常に単純な二重ループにしてみました。
TLEが発生する提出をすればする程ペナルティが付くので、本来は提出すべきで無い事は分かっていますが、パワーで押し切れる事もある事も知っているので、ワンチャンあるかなと思い提出しました。今後は慎みます。

def function():
    # 標準入力
    N = int(input())
    A = list(map(int,input().split()))
    ans = 0

    # 二重ループによる組み合わせの計算
    for i in range(N):
        for j in range(i+1,N):
            ans += (A[i]+A[j])%(10**8)
    
    print(ans)

if __name__ == "__main__":
    function()

想像に難くなく、TLE(Time Limit Exceeded)になりました。

非常に無意味に愚直TLEを出した結果

提出2回目(コンテスト内)　戦略

TLEが発生したので、愚直計算の手法は早々に諦めます。ここで、一旦計算量の見積もりを行います。
今回の配列Nのスケールは$${2 \leqq N \leqq 3 \times {10}^5}$$であり、それを二重ループにして計算を行うと、最大で$${9 \times {10}^{10}}$$程度の計算量になります。つまり、これは一つ一つ組み合わせを計算して処理する事は不可能という事に他なりません。

$$
\displaystyle \sum_{i=1}^{N-1}\sum_{j=i+1}^N f(A_i,A_j)
$$

そこで、問題の答えでもある上記の式を切り崩し、まとめて計算出来る方法を検討していきます。

式の変形

本式について、もし$${1<{A_i}<5 \times {10}^7}$$であるならば、$${x+y < {10}^8}$$になるので、$${10^8}$$の余りなど考える必要がなく、そのままの値を利用する事が可能になります。つまり、以下の式にする事が出来ます。

$$
\displaystyle \sum_{i=1}^{N-1}\sum_{j=i+1}^N f(A_i,A_j) \\
= (N-1) \displaystyle \sum_{i=1}^{N} A_i 　(但し、1<{A_i}<5 \times {10}^7)
$$

$${A_i}$$の制限を式に合わせた場合、上記式から組み合わせの和が$${10^8}$$を超える組み合わせの個数をカウントする事で、値を導出する事が可能です。ここで$${g(x,y)}$$は$${x+y \geqq 10^8}$$を満たす場合は1、満たさない場合は0となる関数とします。

$$
\displaystyle \sum_{i=1}^{N-1}\sum_{j=i+1}^N f(A_i,A_j) \\
= (N-1) \displaystyle \sum_{i=1}^{N} A_i - 10^8\times \displaystyle \sum_{i=1}^{N-1}\sum_{j=i+1}^{N} g(A_i,A_j)
$$

$$
g(x,y) = \left\{\begin{array}{ll}1 & (x+y \geq 10^8)\\
0 & (x+y < 10^8)\end{array}\right.
$$

上の式の第１項は単なる数列の総和である事から、計算量は$${O(N)}$$であり、簡単に計算出来る事が分かります。つまり、第２項となる$${10^8}$$を超える組み合わせの個数が分かれば目的の答えは得る事が出来る、と考える事が出来ます。

g(x,y)について追及する

第二項で利用した関数、$${g(x,y)}$$について追及します。
これについては各$${A_i}$$に対してそれぞれ計算する必要がありますが、配列全てに計算するのは計算コストが跳ね上がってしまうので、二分探索で求める事にしました。

まず、入力例2で出て来た数値を例に挙げます。配列化したものは昇順ソートすると、以下の形で格納されます。

配列をソートした後のイメージ図

$${f(x,y)}$$の他に、$${f'(x,y)=x+y}$$という式も考えておきます。$${A_1=1}$$を起点に考えた場合、これらは以下図の様に表す事が出来ます。

A1を起点にした時の各関数値

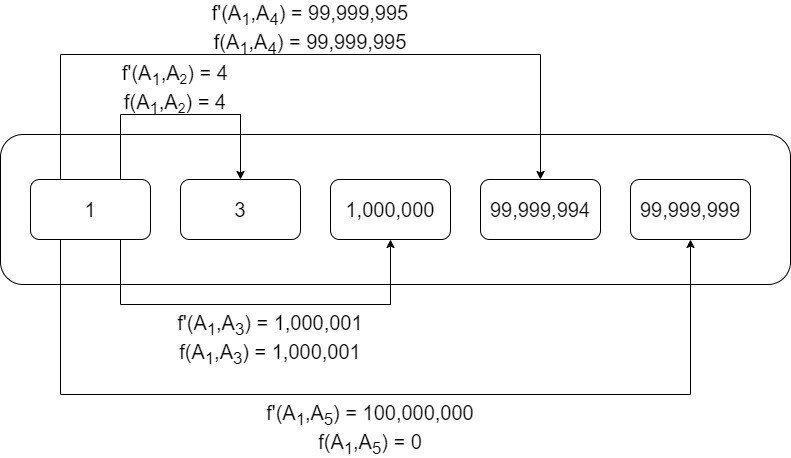
この配列では、$${f'(A_1,A_5)}$$の値だけ$${{10^8}}$$を超えるので、$${f(A_1,A_5)}$$を求める際には$${{10^8}}$$を引く必要があります。そして、$${A_i}$$は昇順ソートしているので、この配列では存在しませんが$${A_5}$$以降の値が存在すれば、それは全て同じ様に条件を満たす数値となります。

つまり、$${ a = 10^8 -1 - A_i }$$の値で配列$${A}$$を二分探索し、その位置以降の値は全て条件を満たす(和が$${10^8}$$を超える)という様にすることで、$${ A_i }$$単位の条件を満たす組み合わせを高速で導き出すことが可能になります。

aの値の位置を二分探索で調査するイメージ図

この処理全体の計算量は、二分探索なので$${O(NlogN)}$$になります。これは十分に高速と言えます。

提出2回目(コンテスト内)　コード

以下のコードで提出しました。

import bisect

def function():
    # 標準入力
    N = int(input())
    A = list(map(int,input().split()))
    A.sort()

    # 二分探索で導出
    k = 0
    for i in range(N-1):
        a = 10**8 - A[i] -1
        k += bisect.bisect(A[i+1:N],a) + i
        
    ans = sum(A)*(N-1) - ((N-1)**2 - k)*(10**8)
    print(ans)
    return

if __name__ == "__main__":
    function()

二分探索はpythonのbisectライブラリを使用して実装しました。内容は上記の通りで、配列は適時最適な形になる様にスライスした配列をbisect.bisectに投入しています。

しかし、この結果はTLEになってしまいました。計算量などを見積もっても問題なさそうなのに、何故？と追及している間にタイムアップとなってしまい、コンテスト内では解くことが出来ませんでした。

提出3回目(コンテスト終了後)

コンテスト終了後ですが、上記回答用コードを見直しました。
そして、原因は以下の箇所にある事が判明しました。

    for i in range(N-1):
        a = 10**8 - A[i] -1
        k += bisect.bisect(A[i+1:N],a) + i

計算量が過剰になってしまった原因は二分探索ではなく、配列をスライスする処理をN-1回分実行している事でした。余計な事をしていた、という訳です。

pythonでの配列のスライス処理は、てっきり$${O(1)}$$だと思っていましたが、実態は$${O(N)}$$なのだそうです。そのまま一部分を利用する訳では無く、内部ではスライス処理を行うと新規の配列に必要な件数分コピーを行っている様で、この一連のforループの計算量は最大で$${O(N^2)}$$前後だった事が分かりました。それだとすると、どうやっても解けません。
提出結果式は以下の様に書き換えれば良いです。

import bisect

def function():
    # 標準入力
    N = int(input())
    A = list(map(int,input().split()))
    A.sort()

    # 二分探索により条件を満たす整数組の数を導出
    k = 0
    for i in range(N-1):
        if(A[i] >= 5 * 10**7):
            k += N-1-i
        else:
            a = 10**8 - A[i] -1
            k += N-bisect.bisect(A,a)

    # 総和計算
    ans = sum(A)*(N-1) - (10**8)*k
    print(ans)
    return

if __name__ == "__main__":
    function()

このコードで提出する事で、無事ACとなりました。

無事AC取れた証拠画像

提出4回目(コンテスト終了後)

実は提出3回目の前に解説を読んだのですが、そちらでは尺取り法で実施していたので、そちらのコードも記載しておきます。こちらもACになりました。

def function():
    # 標準入力と配列の昇順ソート
    N = int(input())
    A = list(map(int,input().split()))
    A.sort()

    # 条件を満たす整数組を尺取り法で導出
    k = 0
    left = 0
    right = N-1
    while True:
        if(left >= N-1):
            break
        if(A[left]>= 5*10**7):
            k += N-left-1
            left += 1
            continue
        while True:
            if(A[left]+A[right] < 10**8):
                k += N-right-1
                break
            right -= 1
            continue
        left += 1
        continue

    # 結果の導出
    ans = sum(A)*(N-1) - (10**8)*k
    print(ans)
    return

if __name__ == "__main__":
    function()

今回のケースだと、こちらの方が速い様に思います。ちょっと記載の仕方をサボっていて、$${A_i}$$が$${5 \times 10^7}$$を超えた後は本来まとめて計算が可能なのですが、コスト的には微量だという事で全部計算させている為、多少コストが上がっています。

尺取り法で解決した時の提出

おわりに

いやー、時間内に解けたなあ…と言う印象。pythonでの配列の取り扱いの悪さが今回ACを取れなかった原因なので、悔やまれる所です。技術的な要素がまだ足りません。

この記事が気に入ったらサポートをしてみませんか？