
FNFE Project #2「Y-E-s-O-d-½」
注意!!集合体恐怖症の方にはきつい画像が含まれています。
FNFE Projectへようこそ!
FNFEは「For New Fractal Enthusiasts」の略です。このコーナーでは「フラクタルに興味があるけど、何から始めたらいいかわからない。。。定義を見ても何が何だかさっぱりだ、、、」という人のために、フラクタルのことを分かりやすく解説していきます。
フラクタルというものを一切知らない人でも、フラクタルの面白さに気付けるように構成しているので、フラクタルが全く分からないという人でも是非読んでみてください!
今回は「反復関数系」について解説しようと思います。
反復関数系とはそもそもなんぞや
直感では分かるのですが実際に説明するとなるとちょっと難しいです。定義としては「歪(ゆが)んだ自身のコピーの集合でつくられるフラクタル」となります。
ひとくちに「歪んだ」と言っても色々あります。単純に移動させるだけ、大きさや向きを変えるだけの場合もあれば、縦横の幅を変えたりぐにゃって曲げることもあります。とにかく一定の関数によって特定の規則に従って歪ませたものを重ねたのが反復関数系に属するフラクタルです。

それで歪ませる→重ねる→歪ませる→重ねる→以下無限ループってやって作ったのがこれです。それぞれのコピーを詳しく見ると、それらもまたそれらのコピーで出来ていて、これがいつまでも続くのが反復関数系のフラクタルです。(実際は無限精度の計算はできないので近似となります)
実例をあげなよ
文だけでは分かりにくいので実例をあげようと思います。#1で出てきたシェルピンスキーのギャスケットで見てみましょう。

同じ形が三つ集まって全体の形を作っています。しかし赤いところをよく見てみてください。全体と相似ですね。青いところも緑のところもそうです。
これは「縮小した自身のコピーの集合でつくられるフラクタル」なので、反復関数系の定義である「歪んだ自身のコピーの集合でつくられるフラクタル」にあてはまります。
同じような要領で作られるこの図形も反復関数系のフラクタルです。ちなみにこれはシェルピンスキーのカーペットといいます。

この場合は元の三分の一の大きさの図形が八個集まってできていますね。
さて、フラクタルは二次元の世界だけにしかないとは限りません。三次元の世界にもフラクタルというものは当然存在します。
代表的なものが「メンガーのスポンジ」で、上のシェルピンスキーのカーペットの立方体バージョンのような形です。

これは一辺の長さがそれぞれ三分の一になった本体が20個集まってできています。
反省文みたいに空っぽな図形
今あげた三つの図形には不思議な性質があります。それは面積や体積が0になるということです。
ではどんなからくりでそんな不思議な事態になるのでしょうか。シェルピンスキーのギャスケットを例にとって解説します。
シェルピンスキーのギャスケットは、次のような手順で作られます。
①正三角形を四分の一の大きさにして、三つ重ねる
②新しい図形をこれまた四分の一にして、三つ重ねる
③あとは②の繰り返し
図で表すとこのようになります。

この図を基に面積を求めてみましょう。元の図形の面積をnとすると、n×$${\frac{1}{4}}$$×3、つまり$${\frac{3n}{4}}$$で次の図形の面積が求められます。$${\lim_{n\to \infty} (\frac{3}{4})^n}$$($${\frac{3}{4}}$$を無限回かける)は0になるので、先述の手順を無限回繰り返してできたシェルピンスキーのギャスケットは面積が0になる、というわけです。
同じ理屈でシェルピンスキーのカーペットやメンガーのスポンジも面積や体積が0になります。輪郭だけあって中身は存在しない図形なんですね。
さらに!メンガーのスポンジの表面積はなんと無限になるのです。穴を空けた回数をnとすると、メンガーのスポンジの表面積は$${2(20/9)^n+4(8/9)^n}$$と表されることが分かっています。このnを1,2,3,4….と増やしていけば、表面積も8, 約13, 約25, 約51とどんどん増加していき、無限回穴を空けた理想状態のメンガーのスポンジでは、表面積も無限大となります。メンガーのスポンジは体積が0で表面積が無限の不思議な立体図形ということですね。
雪が降りしきる町にて
次は線分を変形させてできる「コッホ曲線」とそれに付随する平面図形「コッホ雪片」について紹介します。
まず、コッホ曲線とコッホ雪片はそれぞれこんな形です。

コッホ曲線を三つ合わせたものがコッホ雪片というわけです。始めにコッホ曲線を解説します。
コッホ曲線は以下のような手順で作られる図形です。
①線分を三分割する
②中央の線分を正三角形のような形に変形させる
③線分が四つ出来るので、それらについても①②を同様に適用する
④あとは①②③を無限に繰り返す
図で表現するとこのようになります。

これを繰り返すとこうなっていき

最終的に一番に出てきたコッホ曲線になるというわけですね。

コッホ曲線の長さは(3/4)ⁿと表されます。※nは手順を繰り返した回数
コッホ曲線は手順を無限回繰り返したものなので、n→∞となり、長さも無限大に発散します。コッホ曲線の長さは無限大となるのです。
それでは、コッホ曲線を三つ繋げた図形のコッホ雪片の面積はどうなるでしょうか。無限が三つ合わさっても無限なので、周長は当然無限なわけですが、面積は特に無限大になるようには見えません。実際計算してみましょう。

最初の正三角形の面積を1とすると、次のステップで増える面積は1/9×3で1/3、二回目の変形で増える面積は1/81×12で4/27、三回目の変形で増える面積は1/729×48で16/243となります。
一般化すると、n+1回目の変形では(4ⁿ)÷(9ⁿ×3)だけ面積が増える、とわかります。この級数(一定の法則に従う無限個の数を全て足したもの)がわかれば、コッホ雪片の面積も分かりそうです。
ではこれの級数はどんな数に収束するのでしょうか。
詳しくは省きますが、$${\sum_{n=1}^{∞}\frac{4ⁿ}{9ⁿ×3}}$$は、0.6に収束します。これは元の三角形から増えた面積の合計なので、元の三角形1の面積を足して、合計の面積は1.6とわかります。
メンガーのスポンジは体積は0で表面積は無限大でしたが、こちらは面積が有限で周長が無限大の図形ですね。
ドラゴンに乗って旅に行こう
引き続き直線を曲げて出来る図形を紹介します。

これはドラゴン曲線です。#1でもちょっと触れましたね。ドラゴン曲線は名前の通り龍の尾や爪に似た形をしています。
作り方は線分を一定の規則に沿って曲げただけと単純ですが、相似な形が回転して回転して連なっていくという面白い図形が生まれます。
ドラゴン曲線は以下のような動作を無限に繰り返すことで生成されます。

※線は変換させる向きを表すためのものです。
※辺の長さは大きさを変化させないで書くときのものなので、大きさにこだわらない場合は気にしなくて大丈夫です。
あるいは、こんな感じでも表せます。
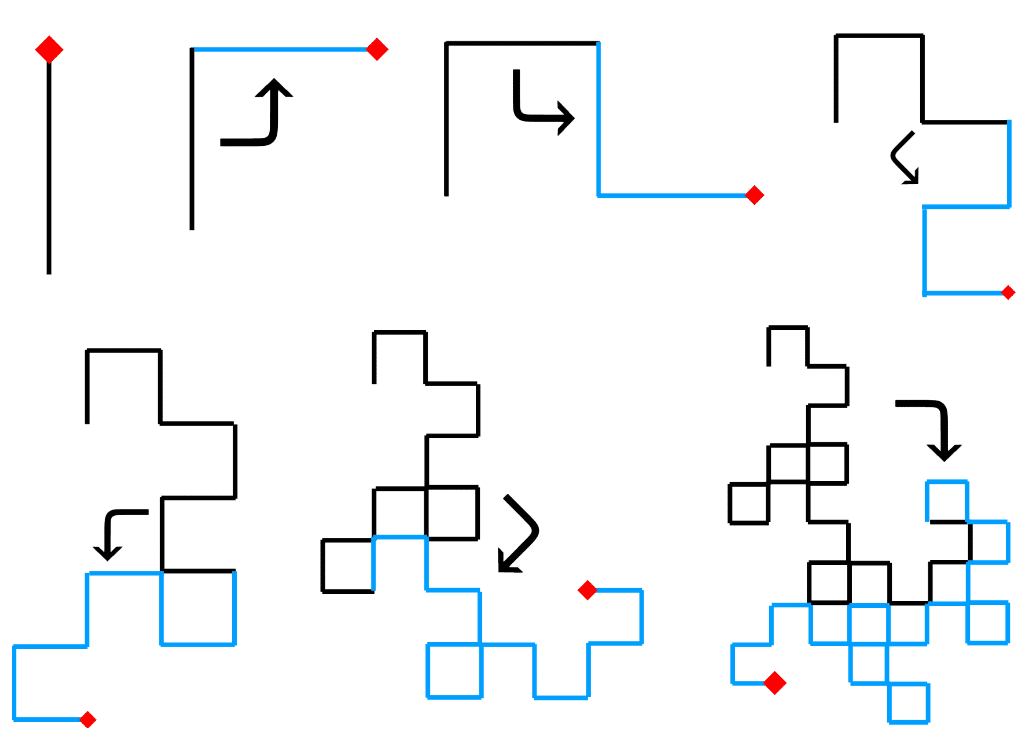
線分の端を軸に90度回転させて重ねる→曲線の先端を新しい軸にする という方式です。これであんな凄い形になるのかと驚きですね。
ちなみにドラゴン曲線はタイル張りできます。色々種類はあるので調べてみてください。

ちなみに、これをこうすると。。。

こうなります。

ちなみにこれを「レヴィC曲線」といいます。右上、左上にドラゴン曲線の先端と似たクルクル模様が見えますね。
レヴィC曲線と関係の深いフラクタルの「ピタゴラスの木」は三平方の定理の図解を基にしてできたフラクタルで、先端部分がレヴィC曲線と酷似した形状をしています。

ちなみにこの四角形の大きさの比を変えると別の形が出てきます。難しくなるので次回解説予定です。
まとめ
いかがでしたか?今回は反復関数系の図形について取り扱いました。
周長や表面積が無限で面積や体積が有限やゼロというのは不思議ですね。
今回取り上げたフラクタルはそれぞれ見た目ではそれほど似ていませんが、基礎となる作られ方は同じです。
次回は反復回数系の応用や描画についてと、L-Systemに軽めに触れられたらいいなと思います。
次回更新は6/30を予定しています。お楽しみに!
参考にしたサイト
※この記事で利用した画像はパブリックドメインのものを拾ってきたか自作です。
おまけ
滋賀?

この記事が気に入ったらサポートをしてみませんか?
