
【フラクタル解説】FNFE Project #13「逃走中on複素平面」
注意!!!独自研究マシマシです。
どうもこんにちは。FNFE Projectへようこそ!
FNFE Projectでは「FNFE=For New Fractal Enthusiast(新たなフラクタル愛好家のため)」という理念の上、フラクタルについて分かりやすく解説していきます。
フラクタルについて全く知らなかったり、記事を読んだだけではなにがなんだかという人も楽しめるので是非読んでみてください!
今回は「マンデルブロ集合の変種」をより詳しく追っていきます。
幾つになっても復習を
何度でもマンデルブロ集合とジュリア集合は復習します。めちゃくちゃ大事なので。
マンデルブロ集合の定義
通常の意味でのマンデルブロ集合はこんな感じの定義です。
・zₙ₊₁=zₙ²+c
・z₀=0 が発散しないような複素数c全体の集合
また発展的な文脈では、f(z, c)を任意の関数と、aを任意の複素数として、このようなものをマンデルブロ集合と呼ぶことがあります。
・zₙ₊₁=f(zₙ, c)
・z₀=a が発散しないようなc全体の集合
一般化されたマンデルブロ集合的な感じですね。
ジュリア集合の定義
一般的に用いられる定義はこんな感じです。kを任意の複素数とした時、
・zₙ₊₁=zₙ²+k
・z₀=c が発散しないようなc全体の集合
より正確な定義としては、cと近い複素数の軌道がcと全く異なるようなcの集合(私たちから見たジュリア集合の端)をジュリア集合と呼ぶそうですがこの定義で使ってる人はマジで見たことがないので上の定義で大丈夫です。
これを一般化して、こんなものをジュリア集合と呼ぶことがあります。
zₙ₊₁=f(z)
z₀=c が発散しないようなc全体の集合
これも発展的な定義ですね。
この記事では特に断りがない限り、マンデルブロ集合は一般的な用法を、ジュリア集合は発展的な用法を意味することにします。
LTNS
本題に入る前に解説おにいさんからいくつか教えたいことがあるそうです。1ヶ月ぶりと前回の登場(#8)から結構時間が経ってしまったので髪が伸びてしまいました。

(解説おにいさん)お久しぶりです。色々解説します。
まず一旦復習です。a+biをzとしたとき、Re(z)はaを、Im(z)はbを返します。
複素共役(ふくそきょうやく)という言葉があります。a+biに対して、a-biのことを共役な複素数といいます。そのような複素数を取る操作を複素共役といいます。(古い文書や書き換えを快く思わない人の文書だと複素共軛と書かれていることもあります)
複素数zの共益な複素数を表す方法はいくつかあり、
①z̄と複素数の上に線を引く
②con(z)と関数で表記する
③z*とアスタリスクで表記する
の3つがあります。今回は主に①で表記することとします。
次に何かの複素数乗やnがマイナスの時のlog(n)の求め方についてですが、これめちゃくちゃめんどくさいです。なぜなら値が複数取り得るからです。
e^iπ=-1という式を基にして求めることが出来るのですが、求めるために変形していると解が無限個取り得る状態になります。
このことについて詳しく解説するとそれだけで記事が埋まってしまうので省くのですが、複素数平面の実軸(実数の軸)、及び原点と解を結ぶ直線の角度(偏角)が-π<n≦πになる解を基本の解である主解として採用することが多いです。(基本の解以外にも無数の解が存在します)
今回描画されるフラクタル図形は基本的に複数解が存在する状況であれば主解を採用しています。
ではさらば。また#14か#15で会いましょう。
ハンドスピナー
短いのに難しすぎる解説おにいさんゾーンを無事くぐり抜けた凄い人たちがここに集結していると思います。ということで本編開始!

ということでまずはトリコーンについて解説します。
トリコーンは、以下の漸化式が無限大に発散しないようなcの集合の事です。
・zₙ₊₁=z̄ₙ²+c
・z₀=0
マンデルブロ集合の式と比較すると、zₙを二乗する前にzₙを共役な複素数に変換していることが分かります。
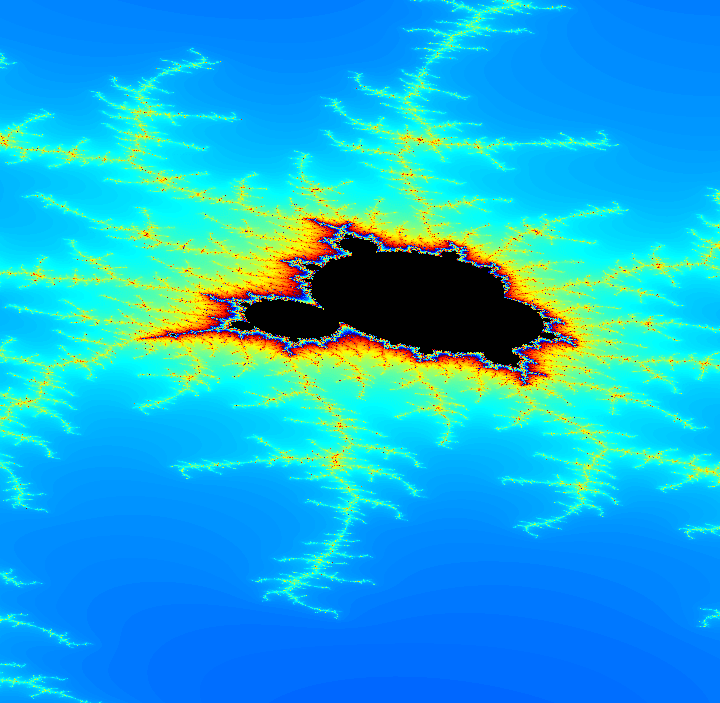
図示するとこのようになります。

見ただけでなんかめっちゃおもろいってわかります。対称軸が3つもあって、引き伸ばされたマンデルブロ集合に似た作りも見られます。
マンデルブロ集合っぽいところと三角形状のところの境目はこのようになっています。

これはバーニングシップフラクタルでも似たような領域がありました。


拡大するとマンデルブロ集合やトリコーンに似た図形が両方現れます。激しく潰されたような形をしていますが、原型は分かります。



中央の三角形のところは拡大してもなんもないです。

これらの飛び地は2つのパターンに分けられるようです。
・トリコーン型
・マンデルブロ型

個人的には、本体から近い場所にマンデルブロ型の飛び地が、そこから少し離れたところにトリコーン型の飛び地が、更に先端に行ったところにマンデルブロ型の飛び地が多いイメージがあります。(仕組みは謎です)

新コーナー!!!!!クイズタイム!!!!!!

(才木珠莉亜)トリコーンのジュリア集合は、どんな形になるでしょう!!!!四択問題!!!!!!

考えてみよう!!
正解発表!!!!

Bの「点対称」でした!!!!



対称の軸が三つならジュリア集合も三回回転対称になりそうだけど、実はそうじゃないなんて面白いね。
何が垂直かは知らん
※ここからの訳はほぼ全て仮訳です。
続いては「Perpendicular Mandelbrot Set(垂直マンデルブロ集合)」を見ていきます。

式としてはこんな感じです。
・zₙ₊₁=(|Re(zₙ)|-i×Im(zₙ))²+c
・z₀=0
この垂直マンデルブロ集合、マンデルブロ・バーニングシップ・トリコーンの性質を全部いい所取りしたみたいになっています。
まず、左に伸びている部分では二つの形が見られます。


上を本体形、下をハート型と呼ぶことにします。
さてこの本体形とハート型の分布、トリコーンで左に伸びているところと対応しているようです。
つまりトリコーンにおいてトリコーン型の飛び地が現れていた領域には本体形の飛び地が、マンデルブロ型の飛び地が現れていた領域にはハート型の飛び地が現れているようです。
気になったので2つの飛び地の境目について調査してみました。するとロジスティック写像との関わりが分かりました。
マンデルブロ集合z²+cの左に伸びてるところにおいて座標z₀は、ロジスティック写像においてa=$${1+\sqrt{1-4z₀}}$$に相当します。
ここで、2つの形の分かれ目にあたる座標はそれぞれ約-1.543689と約-1.788796なので、ロジスティック写像では約3.6785、3.8557が対応するパラメータaだとわかります。
で、このパラメータでロジスティック写像が何をしているのかというと、これはバンドや窓の終わりに相当します。前者はバンドが2つあるカオスの終わり、後者は周期3の窓の終わりに対応しているようです。(仕組みは謎です)
さてこの垂直マンデルブロ集合、上記のトリコーンっぽい性質だけでなくバーニングシップっぽい性質も持ちます。バーニングシップフラクタルで見られるようなモザイク状の領域やめちゃくちゃ引き伸ばされた領域などが見られます。




本体と完全に離れた収束領域やコッホ曲線感のある領域もバーニングシップフラクタル譲りでしょうか。

谷っぽい部分や本体から遠く離れた場所では独自の形が見られました。




ちなみに、こんな領域が出ていたと思いますが、この領域はこんな式で描くことができます。
・zₙ₊₁=(|Re(zₙ)|+i×Im(zₙ))²+c
・z₀=0

これはバーニングシップフラクタルのIm(z)>0の領域を2個くっつけたみたいな形です。

興味深いですね。
適当に色々見てく
ここからは適当に色々見ていきましょう。
次に見るのはBuffalo Fractal(バッファローフラクタル)です。

式としてはこんな感じです。
・zₙ₊₁=|zₙ²|+c
・z₀=0
式や見た目はバーニングシップフラクタルにめちゃくちゃ似ています。バーニングシップでは|zₙ|を計算してから二乗していたのに対し、バッファローではzₙ²を計算してから絶対値に変換しています。
泡状領域、船っぽい領域などが見られます。

他にもこのように独自の領域が見られます。



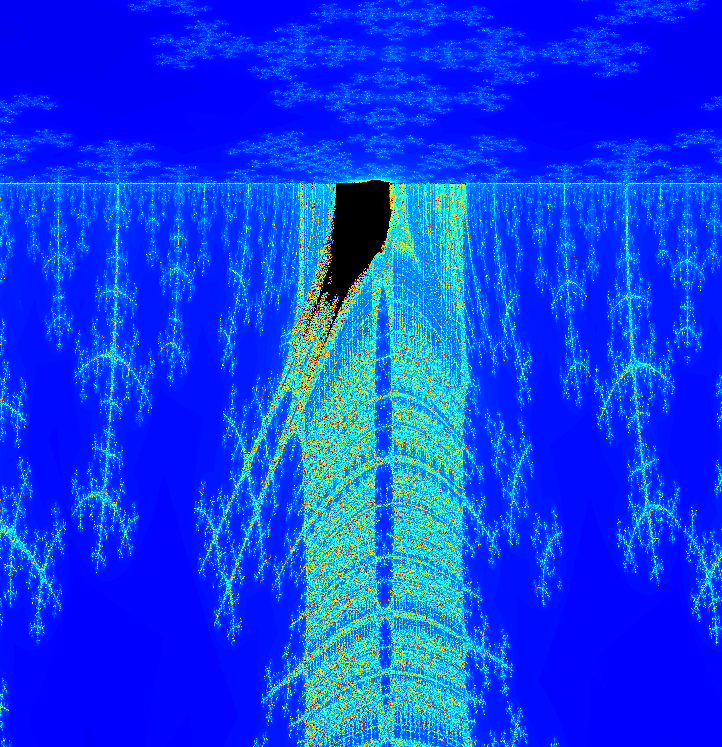
ここからはちょっと無茶苦茶します。これはsin(zₙ)+c、zₙ=0が無限に発散しないcの集合です。

塔形に伸びていく構造など、今までは見られなかったような独自の構造が見られます。

変に壁がぐにゃぐにゃしているのも他ではあまり見られません。

これあれですよね。物語のラストで塵に分解されながら仲間に最期の感謝を述べるやつ。

sin(x)は周期関数なので、こいつらが無限にいます。

谷を進めば進むほどこの黒い筋が増えていきます。


また、この柱はここで不自然に途切れています。

特異点は得意です
次はこれです。
zₙ₊₁=$${2^{z_n}+c}$$
zₙ=0

!??!!!?!?!?!?
ただこれ一個問題があってですね。途中で大きな値が出るので、発散すると誤って判定されるような領域があるんです。
でもそれを何とかできるような彩色法をするとこうなってしまいます。

!?!??!?!?!!?!?!

…ということで、2^z+cのマンデルブロ集合はマジで今までの物とは比べ物にならないくらい描画が難しいです。
描画しやすい図形と描画しにくい図形があるようで、$${k^{z_n}}$$みたいな感じになっているとめちゃめちゃ描画の難易度が上がるようです。
で、何でこんな現象が起きるのかというと、これは特異点が関係しています。
解説おねえさんが解説してくれるそうです。

(解説おねえさん)
ということで特異点について解説します。
特異点とは、関数や数式において微分不可能な状態になってしまう点のことです。
孤立特異点(近くに別の特異点がないような特異点)には3つパターンがあり、今回厄介になっているのはその中でも特に「真性特異点」と呼ばれるものです。
ということで3つの特異点の種類を見ていきます。
はじめに紹介するのは可除特異点です。
可除特異点とは、ある点で定義されないような関数に、その点での値を適当に決めてあげれば、その点で微分できるようになる特異点のことです。
例えば、$${\frac{x^{2}}{x}}$$という式があるとします。この式は普通に計算すればxなんですが、そのままの式で扱うとx=0の時にゼロで割ることとなってしまい、うまくいきません。
そこで、式を簡略化してxにしてあげるか、極限を考えてxに適切な値、今回は0をあてはめてあげれば微分できるようになり普通に扱えるという感じです。
次に見るのは極です。例えば、1/x²みたいな感じです。このグラフではxが特異点である0に近付くとyは無限大に発散していくような挙動を見せます。
特異点aが極なのか判断するにはローラン展開を用います。ローラン展開はこんな感じでやります。
$${f(x)=\sum_{n=-∞}^{∞}a_n(z-a)^n}$$
これで、$${\frac{1}{z^{n}}}$$の形の項が有限個しか出なかったらその特異点は極であると言えます。
そして可除特異点でも極でもない特異点が真性特異点です。真性特異点が厄介なのは、特異点に近付く方向によって挙動が引くほど変わることです。
マンデルブロ集合などではzₙの実部か虚部、どちらかが-2~2の範囲を越えたら必ず発散すると分かっていますが、指数関数のような真性特異点のある関数であればそのような判定が出来ないため、発散するか収束するかの判定が実際に計算するまでできないわけです。
この要因から2ᶻ+cなどはマンデルブロ集合を描くのが難しいのです。
まとめ
いかがでしたか?今回はマンデルブロ集合の変種をいくつか紹介しました。
式の数だけおもしろいマンデルブロ集合の変種があるとわかって楽しかったですね。
また特異点についても知りました。真性特異点があるような関数では、発散判定がうまく機能できないためマンデルブロ集合などを描くことが難しいとわかりました。
今回見たフラクタルらのジュリア集合はあんまりおもしろい形ではなかったためトリコーン以外は載せませんでしたが、他にも無数に変種はあり、当然その分だけジュリア集合も存在します。気になったという人は是非調べてみましょう。
次回、#14は「De Rham Curve(ド・ラーム曲線)」について取り上げます。次回!!!!!!!9月8日(の予定)!!乞うご期待!!!!
※夏休みが明けたのでまた1週間に一度に戻ります。許してください。
参考にしたサイト
👆普段から尊敬しています。
※ジュリア集合・マンデルブロ集合の画像は「Fractal Zoomer」というソフトウェアで描画しました。それ以外の画像はパブリックドメインのものか自作です。
余談
ファンアートは#FNFEFAまでとかよく言ってますけど、投稿されてる瞬間見たこと無いのでマジで投稿してほしいです。
解説おねえさんで検索すると例の組み合わせ爆発の動画出てくるのなんとかしてくれ。ついつい観ちゃうだろ。
