
【フラクタル解説】FNFE Project #26「Void」
謝罪
インフルに病臥していた故25日に公開する予定が遅延してしまいました。インフルエンザが流行ってるので許してください。皆様もご自愛しなさい。
どうもこんにちは。FNFE Projectへようこそ!
FNFE Project「実戦」では、今までのフラクタルの基礎的・標準的な知識をベースに、より踏み込んだことについて探求・探究していきます。
さらには関わりの深いカオス理論・カオス力学系とも絡めながら最終的には複雑系への理解を深めていきます。
今回は「ストレンジアトラクター」を解説します。見てて楽しい分野ですよ~~~~。
そもそもアト(略)
ストレンジアトラクターという言葉を解説する前に。まず上位語のアトラクターとはなんなのでしょうか?
まず時間の変化とともに状態が変わる系を考え、それが取り得る全ての状態を表せる空間を考えます。このような空間を相空間と言います。
どういうことやねん。じゃあまず嫌ほど引き合いに出される単振り子を例に取ってみましょうか。

まず上図のように、シンプルで何の変哲もないただの振り子を考えます。2つのパラメーターで、この振り子の運動の状態を重複なしに記述するためにはどうすればよいでしょうか。
縦・横の位置をパラメーターとしてそのまま記述すればええやろ、と思うかもしれませんが、それでは不完全です。なぜなら左右どちらに動いているか、どれくらいの速さで動いているか分からないからです。

そもそも振り子、紐の長さは変わらないはず。つまり錘(おもり)は一つの弧の上だけを動くので、2つのパラメーターは回転角という1つのパラメーターにまとめることができますね。
では余ったパラメーターで何しようという話なんですが、ここに角速度を追加します。
角速度ということはこっちに回転したら正、あっちに回転したら負というものがあるので、これでどの方向に回転しているかがわかりますね。また速度もわかります。

しかもこうすることで振れ幅が分からないという問題も解決できます。力学的エネルギーから考えて、振れ幅が大きければ大きいほどプロットされる円環も大きくなります。
2つのパラメーターで完璧に振り子の動作を表すことができましたね。これが振り子においての相空間となるわけです。

さてこの相空間を変数の軌道、まあ振り子で言えば錘の動きを辿ると特定の図形を描くことが分かります。また時間を進めていくと軌道はある特定の動きをするよう収束していく動作が見られます。
この時、最終的に引き付けられる軌道を相空間上にプロットした図形がアトラクターなんですね。
難しい話に見えますが、異常に適当に言えばアトラクターというのは周りの軌道が引き付けられ、吸引後はその中に留まる、という領域です。シンプルですね。
力学系の中には連続力学系と離散力学系というものがあり、2つは時間のパラメーターtが連続かそうでないかで分類されます。
振り子など物理的な動きは連続力学系、漸化式など不連続なものが離散力学系ですね。離散力学系の方が考えやすいので主に離散力学系の話をしていきます。
アトラクターはその挙動により4パターンに分類でき、このうちの一つが今回の主題となるわけですね。
➀点アトラクター
②周期アトラクター
③準周期アトラクター
④ストレンジアトラクター
順番に解説していきます。まず点アトラクターはただ一つの点に収束するものです。
摩擦や空気抵抗がある場合、振り子は放置していると段々動きが小さくなり、最後には動かなくなってしまいます。これは角速度0、回転角0の一点に収束する点アトラクターだと見ることができます。
またロジスティック写像もaが0≦a≦3の場合は一点に収束していくのでこれも点アトラクターと見ることができます。


次が周期アトラクターで、連続力学系と離散力学系で姿が変わってきます。
連続力学系では、周期アトラクターは自己交叉がない閉曲線として現れます。

一方離散力学系では、周期アトラクターは変換を一定回数重ねると元の状態に戻る、相空間上の2つ以上の点を順番に循環していくような軌道になります。
例えば以下はxₙ₊₁=3.83xₙ(1-xₙ)という漸化式を、縦軸にxₙ・横軸にnを取りプロットしたものです。xₙが最終的に3つの値を取る軌道に漸近していくことがわかりますね。

続いて、準周期アトラクターは連続力学系ではトーラスの表面に巻き付くような軌道のものを言います。

離散力学系では軌道が閉曲線の形を取ります。

そして最後にストレンジアトラクターです。軌道に自己交叉や複雑さ、不規則性・自己相似性が見られ、初期値鋭敏性が登場します。

二次元

三次元のもの

By Ta2o - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=26810855
驚くべきことにこれらの図形は非常に単純な式から生成されることもあります。ということで次の章ではストレンジアトラクターの実例を見ていきましょう。
ekSAMPLES
まず、以下のような式を考えます。
xₙ₊₁=yₙ+a
yₙ₊₁=xₙyₙ+b
x₀=0、y₀=0
これでaとbをいい感じの値にしてあげると、それだけでストレンジアトラクター完成です。素晴らしいですね!
いい感じの値は、例えばa=1.9、b=-0.45などですかね。これでx,yを座標平面上にプロットすると以下のような図形が表れます。

はい。ストレンジアトラクターですね。これ全部xyが通る点です。よく通る点ほど濃い色で表されています。かっこいいですね。
下部を拡大すると以下のようになります。細かいところで軌道が幾重にも分岐し、自己相似を示しているのが分かります。

またこんなものも考えられます。軌道の重なりやがより分かりやすいですね。
xₙ₊₁=xₙ+yₙ-0.49
yₙ₊₁=1.2xₙ²

こういうストレンジアトラクターは2組以上の変数の漸化式で表されることが多いですね。
名前のついているストレンジアトラクターを順番に紹介していきます。まずはクリフォードアトラクターです。これは以下のような漸化式でx,yを座標平面上にプロットしたときに表れる図形です。
xₙ₊₁= sin(ayₙ)+c・cos(axₙ)
yₙ₊₁= sin(bxₙ)+d・cos(byₙ)



ちなみに、こんな図形を考えてみました。

これはx₀=y₀=0としてパラメーターa,bを変えたもので、モザイク状になっている部分が
・xₙ₊₁= sin(ayₙ)+cos(axₙ)
・yₙ₊₁= sin(bxₙ)+cos(byₙ)
がストレンジアトラクターになる領域、それ以外の領域が点・周期・準周期アトラクターになるものです。いわばクリフォードアトラクターのマンデルブロ集合ですね。
続いてローレンツアトラクターの紹介です。これは3変数のストレンジアトラクターで、相空間も三次元になります。
これは連続時間tと3組の常微分方程式、つまりx,y,zがtの関数で、変数tとx,y,zの導関数が登場する方程式から生まれるアトラクターです。
まず式を見てみましょう。
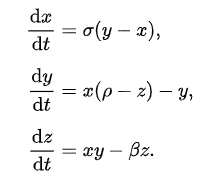
x,y,zに加え、3つのパラメーターσ,ρ,βがありますね。これらを自由に変えて、微分したときに右辺になるような3つの関数の組み合わせを考えます。そしてx,y,zはtの関数なので、tを変えていきながらx,y,zについての上記方程式の解の軌道を三次元相空間上にプロットするとストレンジアトラクターが表れます。これがローレンツアトラクターです。
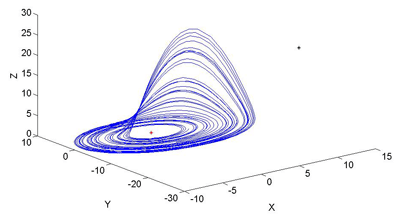
ということで姿を見てみましょうか。

上の図はρ=28, σ=10, β=$${\frac{8}{3}}$$のローレンツアトラクターです。ローレンツアトラクターと言えばこの3つのパラメーター、みたいな認識が強いですね。

ローレンツアトラクターは3次元のストレンジアトラクターで、横から見るとこんな感じになっています。ストレンジアトラクターに対してもフラクタル次元を考えることができ、この場合では約2.06となります。
続いてはティンカーベル写像です。これは以下の漸化式からなるものです。
・xₙ₊₁=xₙ²-yₙ²+axₙ+byₙ
・yₙ₊₁=2xₙyₙ+cxₙ+dyₙ
…なんか見たことあると思った?マンデルブロ集合を複素数を使わず書き直した式に似ていますね。
・xₙ₊₁=xₙ²-yₙ²+a
・yₙ₊₁=2xₙyₙ+b
(x,yはzの実部虚部、a,bはcの実部虚部)
パラメーターはa=0.9, b=-0.6013, c=2, d=0.5という組み合わせであることが多いです。実際にそれで描画するとこうなります。

マジで妖精っぽいですね。ちなみにパラメーターを変えてみるとこんな感じになります。

アトラクターの軌道が2つ以上に分かれる場合もあるんですね。
続いてレスラー・アトラクターの紹介です。これはローレンツアトラクターと似ていますが、生成式がより単純なものとなっています。
$${\frac{dx}{dt}=-y-z}$$
$${\frac{dy}{dt}=x+ay}$$
$${\frac{dz}{dt}=b+xz-cz}$$
ローレンツアトラクターと同様に、連続時間tを変化させながらx,y,zの変化を追っていくとストレンジアトラクターが登場します。
a,bを両方0.1で固定し、cを動かすと以下のようになります。

By Shiyu Ji - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=52901465

By Shiyu Ji - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=52901466

By Shiyu Ji - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=52901478

By Shiyu Ji - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=52901481

By Shiyu Ji - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=52901475
cを大きくしていくと周期が2倍ずつに増えていき、その間隔も狭まっていきます。そして一定地点を超えるとカオスになります。
…あれ????どっかで見たことあるよね????


そうです。ロジスティック写像における3<a<3.5699456地点みたいに、周期倍化分岐が無限に起こるカスケードが発生していますね。
というわけで、例のあの有名な分岐図みたいな感じで描いてみましょうか。a,bを固定してcを横軸に取り、一定のy,zの時、通過するxを縦軸に取ると…

なんかロジスティック写像の分岐図に似ていますね。また、aを0.2、cを5.7に固定してbを横軸に取るとこうなります。逆向き!?なんか斬新ですね。

ちなみに連続力学系がストレンジアトラクターとなるためには3つの変数が必要らしいです。原理は知りません。
続いては池田写像です。池田写像は2つの変数x,yとパラメーターuからなる以下のような写像です。漸化式なので離散力学系ですね。
$${x_{n+1}=1+u(x_n\cos t-y_n\sin t)\\}$$
$${y_{n+1}=u(x_n\sin t+y_n\cos t)\\}$$
$${t=0.4-\frac{6}{1+x_n^2+y_n^2}}$$
これはxとyの変化がそのままアトラクターになるわけではなく、ランダムに初期値を取ってそれが行きつく点をプロットします。

By Accelerometer - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=33235463
これにちょっと似てるけど連続力学系であるものにジャパニーズアトラクターというものがあり、以下のような式で表されます。
$${\frac{dx}{dt}=y\\}$$
$${\frac{dy}{dt}=-ky-x^3+B\cos t}$$

そして最後に紹介するのはグモウスキー・ミラの写像です。今まで見たものとは違い、漸化式の右辺にxₙだけでなくxₙ₊₁が入ります。
$${x_{n+1}=y_n+ay_n(1-σy_n^2)+μx_n+\frac{2(1-μ)x_n^2}{1+x_n^2}}$$
$${y_{n+1}=-x_n+μx_{n+1}+\frac{2(1-μ)x_{n+1}^2}{1+x_{n+1}^2}}$$
……長!!!!
で、これでa=0.009, σ=0.05, μ=-0.801として相空間上に点をプロットすると以下のような図形が表れます。

このストレンジアトラクターは神話の鳥と呼ばれています。かっこよ
他にはこんなものがあります。



ちなみに他のパラメーター2つを固定して1つのパラメーターを動かすと以下のようになります。



ちなみに、グモウスキー・ミラの写像は面白い特性があり、μを1よりわずかに大きい値にし、xₙを横軸、縦軸にyₙを取ってプロットすると…

!?!?!??!?!?!?!??!
注意してほしいのが、これは横軸に反復回数を取っているとかではなくシンプルにxₙを取っているということです。また開始地点は左端、xₙ=yₙ=0.01で、最終的に吸引される軌道は右端の3周期点です。そのころのxₙは276651程まで大きくなっています。
xₙが線形に増えていって最後に周期点に入る、という感じなのですが、非常に興味深いですね。
Re(略)p
今紹介したストレンジアトラクターの多くは、実は物理現象と密接に関係しています。
例えば、ローレンツアトラクターの生成式は大気の状態の変化を非常に単純なモデルで表そうとしたものから生まれています。これは上から冷やされて下から温められる流体における対流を表したものなんです。
またレスラーアトラクターの生成式はできるだけ単純な式でカオスを作ろうとしたもので、上記の式をベースにしているそうです。
またグモウスキー・ミラの写像は粒子加速器内の素粒子の動きを表現するモデルとして考えられたもの、池田写像は「光共振器」という機械の挙動をモデル化したものです。光共振器とは対面させた鏡の中に光を閉じ込め、波を作り出す機械のことです。
カオスというのは意外と身近なところに潜んでいるんですね。粒子加速器は身近じゃねーだろ?確かに。
まとめ
いかがでしたか?今回はストレンジアトラクターについてまとめました。
ストレンジアトラクターは軌道に自己相似や複雑さがみられ、フラクタル次元も持つなどフラクタルの特性を持つことがわかりました。単純な式からあのような複雑な式ができるのは驚きですね。
またストレンジアトラクターの生成式は物理現象のモデル化から来ているものも多く、現実世界との関わりを深く持っていることもわかりました。
次回は以下の3つをやります。
・アルゴリズム作曲
・INT 2/2
・複数状態/近傍拡大CA
#27は2025年1月8日公開です。お楽しみに!!!!!!
参考
予告
こんなフラクタル解説は嫌だ。書き出しがこれ。
注意
この記事に添付されている音声は、人によっては
・人間が聞いてはいけない
・聴く凶器
・頭が割れてとけてあたまがぐちゃぐちゃなきれいでこわれてむこうがわに
・シンプルに癲狂
・無間地獄では(相対的に)夢のような至福
と感じられる可能性があります。

FNFE Project #27「F.T.M.」2025/1/8。
余談
ニーゴのアフターライブが私立入試・特色入試と被ってるのえぐい。
おまけ
ギャラリー。
気が向いたら増やす。



