
31平均律をさらに掘り下げる
ツイッターのアンケートで31平均律についてやっぱりもっと知りたいという声があったので。
ただ基本的なことは前回書いたし、同じこと書いてもしょうもないので前回の31平均律の記事を読んだ人向けに書いていくよ。
周波数比と音程
とりあえずこれを見て。
周波数に対して音程が対数の関係にあるので、純正音程という周波数比を音程に変換するために対数関数を使う。
そのうえで、これらの音程が31平均律の何番目のステップに当てはまるかは前回の画像を持ってくるよ。

オクターブ2倍音は無視で
3倍音→18番 C~G, 完5
5倍音→10番 C~E, 長3
7倍音→25番 C~♯A, 増6
11倍音→14番 C~キF, 長4
13倍音→22番 C~dA, 中6
と雑に覚えておけばいい。
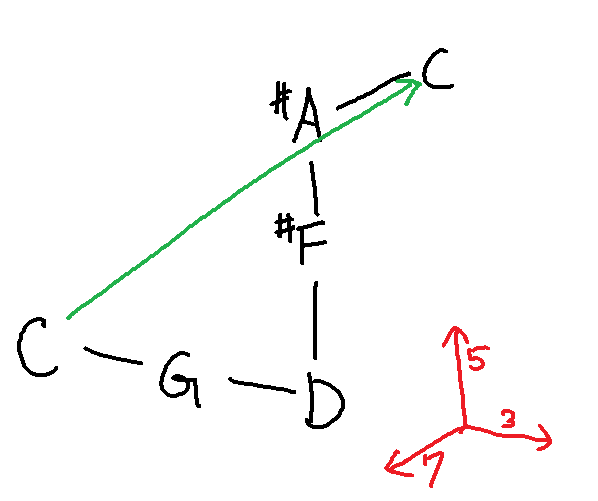
トネッツから格子へ
トネッツ(Tonnetz)とはいわゆるこういうやつ。
でも倍音でこれを見ると、こうなっているともとれる。

そこで勘のいいひとなら気づく事
これ、直交座標にできる!

斜めになっていた軸を起こして直交させられる。
その結果、座標平面に音を置くことができた。
さらに・・・

軸は素数倍音の数に応じて増やすことができる。
特定の音程ごとの堆積を倍音の掛け算軸であらわすことができる。例えば、Cは1倍としたら、Gは3倍、Dは3²倍、というように。
こうして座標空間に素数倍音ごとを軸とした幾何学でいう格子(Lattice)を作ることができる。
オクターブの区別が必要なら別に2倍音軸をとっても構わない。
(というかオクターブ無視の時に軸を省略しているだけ)
音程を素数のベクトルで
空間に表せるということは、音程はベクトルにできる。

例えば
完全5度(3/2)は、2⁻¹×3¹なので、(-1, 1)
長6度(5/3)は、2⁰×3⁻¹×5¹なので、(0, -1, 1)
というように、音程の周波数比を素因数分解して、その指数部分がそのままベクトルとしてみなせる。
音律論界隈では、[-1, 1> というような書き方をして、Joseph L. Monzo氏に肖ってこのベクトルをモンゾという。

ワイは機会あって一回モンゾさんとzoomで顔を合わせたことがある。
純正律では格子に音のダブりはない
実際にこの格子でどこか音がダブるように感じるかもしれないけど、そんなことはない。
素数をいくら掛け合わせても1に戻ることはないから。

例えば、Cから3倍音方向に4進むとEがあり、これはいわゆる81倍音に相当する。ただ、5倍音方向にもEがある。
オクターブを無視するなら、5倍方向のEは2⁴=16を乗算すると80になる。
要するに、この2個のE同士には81/80の差があって、別の音である。
モンゾは[-4 4 -1>になるが、音程としては21.5¢程。同様にこのベクトル同士の音程は全部21.5¢差。
こういう微小な音程が、この座標空間にはいっぱいあって、comma(コンマ)と呼ばれる。先ほどの81/80にはSyntonic commaという名前がある。
コンマの緩和
音が無限に多いとどうしようもないので、どこかのコンマを誤魔化す。
例えば12平均律は
81/80, [-4 4 -1> のsyntonic comma
128/125, [-7 0 3> のdiesis (ダイイシス と読みます。イギリスの競走馬じゃない)
ふたつのベクトルによって、空間が制限される。

実際これはベクトルによって行列を作って、その行列式を計算した場合に絶対値が、ベクトルが作る空間の体積になることが分かっている。
オクターブである2倍音軸は無限に広がっていてもいいので、この軸を無視して行列式を解く。

詳細はヨビノリさんに任せておいて・・・
まあこれをfokkerの周期ブロックっていうんですけどね(適当な邦訳)
31平均律が緩和する重要なコンマ
勝手に重要だと思う緩和されたコンマを拾って特徴を紹介するよ。
syntonic comma
[-4 4 -1>, 81/80
これを緩和できるやつは、「Meantone」と呼ばれ、普通のダイアトニックに向く。なぜなら5度圏(3倍音)を4回進めば5倍音になってくれるから。

septimal kleisma
[-5 2 2 -1>, 225/224
これをただ緩和するだけならいいけど、syntonic commaと一緒に緩和すると、増6度がちょうど7倍音になる現象が起こる。このようなmeantoneを特に「septimal meantone」という。
これを利用すると、例えばⅢ7の裏コードでルートを♭Ⅶへ代理するときに、構成音のルートから3度の♯Ⅴをそのまま残すと♭Ⅶ~♯Ⅴがまさに7倍音に近似するので、まさかの裏コードを♭Ⅶ(#6)とすることで4:5:6:7に近似する。
これは31平均律ユーザーにぜひまねてもらいたいネタなんだけど
— 原井玉葱郎 (@Regret_March) May 16, 2023
Ⅲ7の和音の裏、♭Ⅶ7を取るときに、Ⅲ7の3度の音を♭Ⅶ7の7度に変えずそのまま残しておくと、セプティマルミーントーンの特性上ハーモニック7thになるよ pic.twitter.com/bgmXdzUSZz
gamelisma
[-10 1 0 3>, 1029/1024
完全5度1つ進んでから、7倍音を3回堆積するとできる「gamelisma」
緩和すると5平均律のようになることから、このような音律はスレンドロ音階に準えて「Slendic」と呼ばれる。

これがあると、完全5度を3等分でき、mothra[6]というまた辺鄙な旋法を組める。
rastma
[-1 5 0 0 -2>, 243/242
このコンマを緩和すると、11/9、おおよそ中3度を2個積むと完全5度に。
ニュートラルスケールは、中3度圏の7個の堆積からできるので、ニュートラルスケール(中調)が取れる場合必然的にここを緩和している。


マカーム(またはジンズ)のrastが由来になっている。
mothwellsma
[-1 2 0 -2 1>, 99/98
これは増2度(7/6)を2回堆積すると、長4度になる性質。

9回堆積していくと、orwell[9]という旋法ができる。

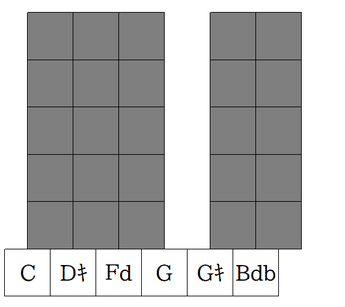
音程を31平均律のステップに直す便利ツール
ヴァル
31平均律では、オクターブを無視せず、
2倍音が、31ステップ
3倍音は、31+18ステップ
5倍音は、31×2+10ステップ
7倍音は、31×2+25ステップ
11倍音は、31×3+14ステップ
13倍音は、31×3+22ステップ
となるので、音律の近似ステップ数でモンゾとは意味の異なるベクトルが作れる。この場合、
<31 49 72 87 107 115]
という感じになっている。
このベクトルをヴァルと言い、モンゾと合わせると本領発揮する。
例えば、長7度を純正音程15/8とみて、この音程をモンゾに表すと、
[-3 1 1> になるので、これをヴァルと組み合わせて内積を取る。
<31 49 72 87 107 115][-3 1 1 0 0 0>
=31×(-3) + 49×1 + 72×1 = 28
28ステップはちょうど31平均律の長7度になる。
このように、ヴァルを使うと純正音程がどこに近似されるかが計算で分かる。
もちろんここに緩和されるコンマを入れると、それらは同音扱いなので内積0になる。
ワイにうまい棒を恵んでくれると飛んで喜びます。
