数学には「革命」が起こるのか？

~JUDITH V. GRABINER ，“IS MATHEMATICAL TRUTH TIME-DEPENDENT? ”
を読みながら~

序．

　科学は「進歩」するものですが，その歴史を考えるとき，例えばアリストテレスやプトレマイオスの「間違い」をあげつらい，彼らを現代の基準で裁くということに賛成の人は少ないと思います．つまり科学は「パラダイム（ここではその時代や地域で規範となる事物の見方や捉え方ほどの意味としましょう）の転換」を経験し，現代に至るという理解は広く認められていると思います．しかしながら，数学においてはパラダイムの転換が起こるのかは，いまだに合意に至ってはいない，もしくはそういった興味すら持たれていないと思われます．それどころか「数学史」と称する本を開くと「数学の歴史とは，過去から現在へと直線的に発展した大いなる歴史である」として語れているものもあります．
　本稿では，このことを問題にした　JUDITH V. GRABINER
“IS MATHEMATICAL TRUTH TIME-DEPENDENT? ”（1974）という論文をもとに，数学の歴史とはどういったものであるかを考えたいと思います．

1．問題提起

　まず，経験科学における「パラダイム転換」を提唱したクーンは，当初は数学にはパラダイム転換は起こりえないという立場だったとされますが，Philip Kitcherらの主張に促され，数学にも「転換」が起こりうるという立場をとるようになったようです¹．

Grabinerの論文の要旨は，
1．「ギリシャにおける幾何学の公理化」→「形と数」の経験科学から「数学」への変化
2．「非ユークリッド幾何の発見」→数学が扱うモノの変化
3．「厳密な定義への指向」→数学の基礎の見直し
という「革命」が起こったという提案です．

まず，この式を見てください．

(x - a)(x - b)(x - c) = x³ -(a + b + c)x² +(ab + ac + bc)x - abc

この当たり前の式ですが，かつては幾何学（図形）的な説明を介さない限り証明とは認められないと考えられていた時代がありました．例えば3次と2次の代数の和や4次以上の代数方程式は幾何学的には意味をなさないため証明ではなかったのです²．

では，なぜこの式を「正しい」と17世紀の数学者は考えたのでしょうか？
それはニュートンに言わせると代数は「普遍算術」であるからということになるようです．代数による証明を認めるか否かという現代の我々には理解の難しいテーマですが，ここに「事物の見方や捉え方」の変化が認められるのです．

また著者は，有名な「オイラーの公式」の発見過程には，見逃せないギャップ（無限小×無限大＝有限値？）があることを指摘します．
（※数式がつらい方は飛ばしてください）

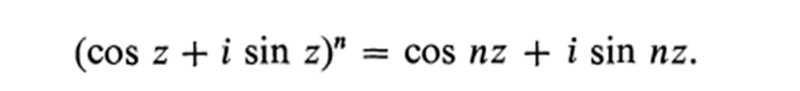
nは無限大であり，ｚを無限小としますが，その積（！？）を計算すると
ｎ×ｚ＝ｖという有限値ｖを取るというのです．現代ではこういったナイーブな計算は許容されていません．現在，「オイラーの公式」の証明として教科書に書かれてあるものにギャップはありませんので，それはより「厳密」に書き換えられているものなのです．
　この例のみならずこの時期の数学は現代の基準で裁くととても「お粗末」であるとし，こう総括します．

「17世紀末に微積分が発明されると，結果を求める意欲は際立ち，強力で新しい方法が広大な新世界を征服することを約束しました．ここで太陽系全体の運動方程式を解くこと程に刺激的な仕事はないだろうと想像できます．微積分は新しい結果を導き出すための理想的な道具でしたが，多くの数学者は何故この道具が機能するのかを正確に説明することが出来なかったのです」

　ではこの時代の数学者を「いい加減な輩」と評価することが適切でしょうか？　著者はこの時代の数学者の得た結果は驚くほど正確であったと評価しています．彼らは鋭い直感があり，結果の検証に十分な関心をもっており，それを支える社会制度もあったと説明されます．
　さらに，オイラーの「いい加減な」無限の代数も，彼は「普遍代数」の一分野として理解したため十分に証明されものとして扱うことができたのでしょう．著者の指摘するこの時代の数学の「ギャップ」は，我々にとっての「厳密の基準」で裁いてこそギャップになるのです．

2．パラダイム

　ここで著者は数学者がパラダイム（という言葉を用いず論文ではexistential situationと表現します）の中で数学をしているという解釈をとるべきだと提案します．経験科学として誕生した数学は，ギリシャにおける証明の発明により経験科学から変貌し，代数による証明を認め，微積分の発明により豊富な成果を得た，また扱う対象が非ユークリッド幾何のような「（当時の人にとっての）現実世界」とは接点を持たないモノに変化していく．数学が現実世界とは無関係に展開するというのは現代では当たり前かもしれませんが，数学とはアリストテレスに言わせると「形や位置など感覚可能なものを手掛かりに」した学問でした³．ここにも「事物の見方や捉え方」の変化が認められるでしょう．数学にはこのようなパラダイム転換（もしくは大変動）があったというのです．
　では，数学の歴史にパラダイム転換がないとすればどういった歴史を語れるでしょうか？「円周率」を例にしてみましょう．

「昔々，古代エジプト人は円周率をうまく計算することができなかったので円の面積を正方形のタイルを置くようして近似していましたが，時代を下るとエジプト人よりも賢いアルキメデスが円周と半径の積であると証明し，素晴らしい近似計算を行いました．その後もアルキメデスの方法を真似して中世の凡人たちは近似の精度を上げていきましたが，微積分の発明により無限級数によりπを評価できるようになり，さまざまな加速法が発明され人類は円の面積をいくらでも詳しく求められるようになりました．さらにコンピュータの導入により…云々．このように人類は円周率についての知識を深めていったのです」

このような歴史（物語？）を人類の進歩の大いなる物語として語ることになるでしょう．実際にベックマン『πの歴史』はこういった内容です⁴．

　これで過去の数学者の思想や思考を理解したことになるのでしょうか？過去の天才の発想を理解するには，彼らがなした結果ではなく問題解決の技法に注目し，どのような枠組みの中で数学をしていたのかということの解明こそが重要だといえるのではないでしょうか．
　エジプト人の面積計算とエウクレイデス『原論』の面積についての証明を，同じ面積を扱っているからといって，エジプト人よりもギリシャ人の方が厳密さにおいて発展としていると捉えるわけにはいかないのです．両者は別のパラダイムの中で数学をしているのです．

3．まとめ

　著者は「数学的真理は永遠であるかもしれないが，それについての私どもの知識は永遠ではないのでしょう」とし，「数学は革命のない唯一の科学ではありません．むしろ数学は破壊的な度合いは最も少ないが，それでも最も基本的な革命が起こっている人間の活動分野なのです」とまとめます．
　もちろん数学における大変動の起きた時期について，著者の提案に完全な合意があるわけではありません．さらに「ギリシャ→西洋近世→近代」という図式で数学史を語る問題点もあるでしょう．
　それでも著者の提案した数学にはパラダイムがあるという解釈は数学史を魅力的に語る方法であると思われます．

注釈

1）この経緯については佐々木力『科学革命の歴史構造 上』序論を参照してください．
2）この幾何代数から代数への変容は，本稿とは異なる立場で書かれた本ですが，木村俊一『天才数学者はこう解いた、こう生きた 方程式四千年の歴史』が楽しい読みものです．
3）このような古人の数学観はアリストテレス『形而上学』を参照．
4）ベックマン『πの歴史』は，数学者が歴史書を書くとどうなるのかということの分りやすい例としては秀逸な例となっています．