
古代の数学に「円周率」はあったのか?
序.
「円周と直径の長さの比率」である「円周率」は π とも呼ばれ,最も有名な数学定数の一つですが,この定数はいつ頃から数学で扱われるようになったのでしょうか.本稿では,最古の数学であるエジプト数学¹やバビロニア数学には円周率という概念はないこと,さらに西洋古代の数学にも見られないという話をしたいと思います.
しばしば,古代の円の面積を計測する議論(以降では「求積」と呼びます)の説明に,「エジプト人は円周率を約3.16として計算した」と説明されることがあります.この説明は不適切であり,「エジプト人は円周率を約3.16として計算したように我々は見ることができる」とすべきなのです.
些細な違いに思われる方がいるかもしれませんが,本稿はその「些細な違い」の重要性について説明するものです.また,現代の概念を古代に見出すことの意義と不適切さについても検討します.
1.エジプト人の仕方
まずエジプト人の円の求積について確認しておきましょう.直径9の円を八角形で「近似」する仕方です.ここで「近似」という言葉を使いましたが,彼らが本当に近似と考えていたのか,その証拠はありません².円の面積の「真の値」を知っている我々にそう見えるというだけです.

我々は円の面積の公式が(半径)×(半径)×(円周率)であることを知っていますから,このエジプト人の得た結果から
(2r×8/9)²=256r²/81=πr² となり,π≒3.16 が得られます.
一般に「エジプト人は円周率を約3.16とした」という言説の根拠はこれです.しかし上記の計算手続きのどこに「円周率」があるでしょうか?エジプト人は円周と直径の比率を用いずに円の求積を行っているのです.エジプト人の円の求積に円周率を見出すのは,積分を知らない人が行った三角形の面積の計算をみて「実はその計算には定積分の概念が潜んでいる」という程に無意味なことをいっているのです.
なおパピルスに残された図版はこのようなものであり,七角形にも見えます.これまでの議論は,エジプト人は八角形を用いて円の求積を行ったに違いないという現代の想定をもとに復元されたものなのです.

またバビロニア数学においては,直径ではなく円周を用いて円の求積は行われますが,そこでも「円周と直径の比率」が計算の過程にでてくることはありません.次に古代ギリシャを見てみましょう.
2.アルキメデス
円の求積を世界で初めて"正しく"行ったとされるアルキメデスの仕方を見てみましょう.アルキメデスは円の面積を次のように表現します.
すべての円〔の面積〕は,まず半径が直角を挟む一辺に等しく,また円周が底辺に等しい直角三角形〔の面積〕に等しい.
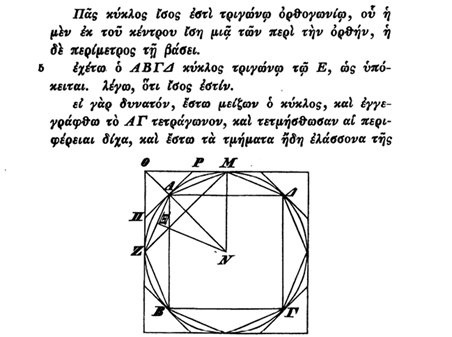
言葉で表現するため分かり難いですが,現代風に解釈すれば[円の面積]=[半径]×[円周]÷2 といっているわけです.これを「取り尽くし法」という仕方により厳密に証明しました.ここで人類は円の「真の面積」を知ることになったわけです.この結果により,円周の長さが分かれば円の真の面積を知ることができるということが明らかになったのです.
では円周の長さはどうやって知ればよいのでしょうか?そこでこれ以降,円周の長さを精確に求めることが「精密な円の求積」の主題となります.そしてアルキメデスも内接・外接多角形の周長を計測することによりいくらでも精密な円周の長さを求めることができることを示したのです.

しかし,ここでも注意しないといけないのは,アルキメデスは円周の長さを求めただけで,それを直径で割った比率には関心がないのです.これまで見たように,古代の円の求積には「円周を直径で割った値」は必要ないのです.さらに重要なことですが,アルキメデスは円の面積を(直径)×(円周)÷2 と表わしません.円の面積は,半径を高さとし円周と等しい底辺をもつ直角三角形の面積に等しいのです.幾何学の証明に算術の概念である「加減乗除」は用いられません.
このように西洋古代における円の求積は,円と正方形,または円と三角形の比較であり,そのために円周を計測することはありましたが,円周と直径の比率を議論した例はありませんでした.
3.精密さか便利さか
円周の長さの計測は天文学や工学においても重要であったため,アルキメデスによる円周の評価以降も,その探求と利用は続けられてきましたが,その実情をみると,やはり「円周率」という概念が見られないことが分かります.
紀元後2世紀の天文学者プトレマイオスは,円周率を377/120(小数で表わせば3.14166…)と計測したと説明されますが,これも注意が必要です.彼の著作『アルマゲスト』のどこを見てもそのようなことは書かれていないのです³.
プトレマイオスは,半径60の円において 1/2度の円弧が張る弦の長さ(三角比で表現すれば 2×sin0.25° の大きさ)を,31/60+25/60² (小数では0.523611…)としているだけです.ここから逆算した結果を小数で表わすと,π=3.14166… がでてくるのです.

また,西洋古代の円の求積や円周の求長がすべて「精密さ」という同じ方向へ「進歩」していたわけではありません.円の面積を(8d/9)²としたエジプトも,ヘレニズム期には(3d/4)² としています.アルキメデスによる精密な評価の後にもかかわらず,半径1の円の面積を 3 としているわけです! 必ずしも精密な求積が歓迎されたわけではないのです.
またローマの建築家らも円の面積や円周の長さを利用していますが,やはり円周率の利用はありません.まず円周率を 3.125 としたとされる紀元前1世紀の建築家ウィトルウィウスを見てみましょう.
四輪車についている車輪が中心を通る直径で4ペース(約29.6cm)
の寸法であるとする.そうすると,車輪が輪の上に一定点をもっていて,そこから前進して路上面に転がりはじめるとき,まわりはじめたところからこの定点に到達することによって12ペース半の精確な走行距離の尺度をもつことになる.
ウィトルウィウスは円周率の話ではなくオドメーターの話をしているのが分かります.4ペースの車輪の円周が12.5ペースとすら言っていないのです.その走行距離が12.5ペースになるというだけです.我々は「直径に車輪の回転数と『ある定数』を乗じれば,走行距離が分かる」という表現がないということに注目すべきであり,つまりウィトルウィウスは車輪の周囲と直径の比率には無関心といえるのです.

さらにもう一例見ておきましょう.紀元後1世紀のフロンティヌスは水道管の太さについて議論しています.円管の断面積により水量を計算するため,その大きさを知ることが必要ということのようです.
正方形の平方ディギトゥス(約18.5 mm)は円ディギトゥスに比較して,正方形の大きさの3/14大きい.一方,円は正方形より円の大きさの3/11だけ小さい.
やはり円周率はでてきませんし,そもそも円周すら利用されません.円の面積は正方形を3/14だけ削ったものに等しいと言うのです.以下のように円周率を逆算することはできますが,もちろんフロンティヌスにそういった関心はありません.

このように円の求積の仕方は実に多様で,精密さを重視した人もいれば,計測の利便性を重視した人もいます.西洋古代には「円周率」という図形から独立した概念はなく,その精度を高めるといった努力はなされなかったと解釈すべきでしょう.
さて,しばしば文明退化の「象徴」とされる,直径1の円周を3とする仕方も,実際に井戸を煉瓦で囲むことを考えると非常に便利であることが分かります.円周が 3.14 では隙間にコンクリートを流し込めません.この便利さを我々の基準で「退化」とするのはまったくナンセンスな歴史の見方といえます.

このように古代の数学における円の求積は実に多様であり,「円周率」という我々の概念を過去の数学から勝手に「発掘」し,その出来映えを「鑑定」する作業は歴史の見方としてはあまりにも貧弱といえるのです.

4.「大きさ」から「量」へ
それでは,いつ頃「円周率」という概念は発明されたといえるのでしょうか?このことを考えるのに重要な点として,幾何学が扱う対象が「大きさ(magnitude)」から「量(quantity)」に変化したことに注目する必要があります.既に2章で言及しましたが,古代の幾何学には「加減乗除」といった演算・操作は認められていませんでした.これを不思議に思われる方もいるとは思いますが,そもそも「縦×横」とは一体何でしょうか?それを「長方形(の面積)」であると見なすという発想は古代にはなく,そのような図形の見方の変化は,計算が幾何学に侵入することにより徐々に起ったものであり,数学に「革命(パラダイム転換)」を起こした大変化の一つでもあるのです.
その変化の徴候として次のラテン語の詩に注目してみましょう.円周率の記号が発明されるまではこの「詩」により円周率を表わしていたようです.
Quantitas, in quam cum multiplicetur diameter, proveniet circumferentia.
〔円の〕直径に掛けると,円周の長さになる,ある量(quantity).
(直径)×(ある量)=(円周)といっているのです.これは古代数学の表現とはまったく異質な発想です.ここでは円周率が明確に「ある量(quantity)」として認識されています.その後,ニュートンと同時代のウィリアム・ジョーンズにより 円周率を表わす記号πが導入され現代に至るのです.この「大変化」以降,πの探求は図形を離れた量の問題となり,解析学(微分積分学)の仕方によりその精度を上げていくことになるのです.

図形そのものの「大きさ(magnitude)」にしか関心のなかった古代の数学ですが,そこに円周率という「量(quantity)」は見当たりません⁴.それが次第に代数計算が幾何学に侵入することで,図形のもつ「量」が発見され「円周率」という図形とは独立した概念の発見に至るのでした.
5.現代の概念を過去に見出す意義
それでは何故,円周率という概念を古代に見出してしまうのでしょうか?
ここで「遠近法」という概念との比較により検討してみましょう.
しばしば「遠近法はルネサンス期の発明である」と説明されますので,古代の美術作品に遠近法は見られないということになります.しかし西洋古代にも遠近法はあったと考えるべきです.まず,この古代に描かれた壁絵を見てください.


現代の遠近法では一つであるはずの消失点が複数個あるのがわかります.
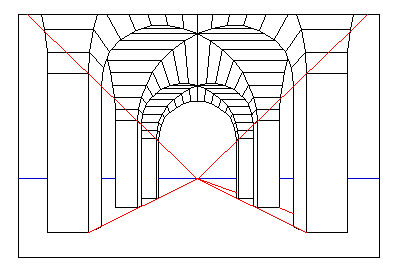
よって,このポンペイの壁絵は透視図法(一点透視図法)ではありません.しかし幾何学的な工夫により遠近感を表現しているのはよく分かると思います.つまり古代には「一点透視図法としての遠近法」はなかったと考えるべきなのです.古代人も,一点透視図のような絵を描きたかったが,未熟だったので仕方なく陰影法や消失点が複数個ある絵を描いていた,と評価すべきではありません.一点透視図が表現する世界の見方は普遍的なものではないということに注目すべきです.
遠近法という概念や技法は古代よりあったが,「一つの消失点」という発想や技法はルネサンス期の発明であったということになります.これは円の求積の歴史において,古代より円の求積は様々な仕方により行われてきたが,「円周率」というのは近世の発明であるということと相似形になっています⁵.

数学の歴史は,「問題」とその「解決の技法」に注目して記述すべきであり,円周率や三角関数といった概念に注目すべきではありません.そして,このことへの無理解が,円周率という概念を古代の数学から発掘し,鑑定してしまうという「悪習」の原因といえるのです.
おわりに
古代の数学に円周率(円周/直径の定数)はみられないというお話を以前しましたが「円の求積を行っているからには,円周率という概念をもっていたはずだ」という方々は,今後も後を絶たないかもしれません.しかし,これはとても不適切な歴史の見方だといえることがお分かりいただけたと思います.
というのも「円周率の概念の有無」は,円の面積=πr² であり,必ず円周率を用いなくては真の値を得たことにならず,それ以外の仕方での求積――エジプト人やローマ人の仕方――を「円の求積」と呼ぶことはできない,という文脈でこそ議論すべきなのです.そして,そのような歴史の見方は実りのないものになるでしょう.
現代の数学では「(円の)面積」というのは操作的な定義(面積とは何かが数学的に定義されたもの,例えばリーマン積分のような)が必要であり,その定義(操作的な定義)に従って決定されます⁶.そうではない仕方で行われるものを厳密には面積とは呼べません.すると積分が定義された時点で求積ができるようになったということになります(古代ギリシャ数学に面積や長さの定義はありません).
この考えをもとに過去の数学を眺めると,古代の円の求積や近世の体積の計測は,なにか「それっぽいこと」をやっているだけで,求積ではないことになるでしょう.これが現代の基準で過去を測るということの帰結です.しかし数学にも革命(パラダイム転換)があったとすれば,現代の基準で過去の数学を測ることはできませんので,過去の数学にも求積はあったといえます.操作的な定義を必要としない過去の数学においては,現代とは異なる求積法が確かにあったといえるのです.
数学には「革命」が起こるのか?|古代ギリシャのヘルメス|note
古代人は,円の求積をするにあたり,彼らの数学の枠組みの中で,円を正方形や三角形,長方形に置き換え,もしくは帰謬法により我々であれば「区分求積法」と呼ぶ仕方で,「彼らの求積」に取組んでいた.しかし彼らの円の求積に,円を扱っているのだから円周と直径の長さの比である「円周率」という概念が実は隠されているというのは無意味です.
円周率の意味が変化を被ったのではなく,数学という学芸のあり方や,幾何学において扱う対象が「大きさ」から「量」へ変化することで,求積という概念の意味,技法の目的が変わったといえるのです.
注釈
やや専門的な内容を補足しておきます.
1)エジプト数学:古代エジプト文明における数学で,ギリシャ数学を受容したプトレマイオス朝時代のものを含む場合もあります.また,円柱の容積を計測する問題においては底面積を求める際に,直径から1/9を引いたものを2乗します.ここでも円周率という発想は見られません.
2)近似:エジプト人の数学テクストには手続き以外の一切の説明はありませんので,彼らが得た結果を近似と考えていたかを判断する史料はありません.なお古代ギリシャ語には「近似」という語が一つあります.アレクサンドリアのディオファントスが『算術』において παρισότης という語を使っており,これが「近似」と訳されます.しかしこれは「なるべく近い自然数を選ぶ」という意味であり,我々の想定する「真の値と近似値」とはまったく異なるものです.そのためヒースによる英訳版では,この単語はギリシャ語のままにされています.T.L.ヒース(平田寛 訳)『ギリシア数学史』共立出版(1959年)404-5頁を参照してください.
3)ベックマン『πの歴史』ちくま学芸文庫(2006年)は歴史書としては大変に問題の多い本です.126頁には,プトレマイオスは π=3+(17/120)=3.14167 としたと書かれてありますが,その典拠は示されていません.この例のみならず,典拠不明の記述が散見されます.日本語版ウィキペディアの「円周率」には出典としてベックマン『πの歴史』が挙げられているが,以上の理由によりその大半が無効なので注意が必要です.
4)量のない幾何学:ギリシャ数学は図形のもつ大きさを比例関係により表現します.つまり,A:B=C:Dという関係は,A/B=C/Dを意味しません.そしてこれまで確認したように,円周:直径=X:Yという関係の探求や利用はギリシャ数学にはみられないのです.この違いを明確にするため A:B=C:Dを,A:B::C:D と表わす習慣もあります.
5)円周率の発明時期:図形から「量」を取り出すようになったのはいつ頃なのでしょうか.16世紀の最高の数学者の一人であるルカ・ヴァレリオの著作では図形の「大きさ」と「量」が区別されていない状態が認められます.一方,1566年にピッコローミニの著作には,幾何学の対象(すなわち図形)が「量"quantità"」をもつという言及が現われます.しかし,その「量」は図形から独立したものではなく,図形に付帯するものとされているようです.16~17世紀の間に,徐々に図形に「量」を見出すようになり,その考え方が浸透していき「パラダイム転換」が起ったのだと考えられます.そしてその時期は,代数計算が幾何学の証明として認められる時期にほぼ一致します.それまでは代数計算は幾何学的に証明されることではじめて正当な議論と認められていましたが,ここに至り代数と幾何の立場が逆転することになるのです.よって西洋においては,この時代に「円周率」は発明されたと想定できるのかもしれません.
6)操作的な定義:現代数学において「円周率」は「円周と直径の長さの比率」として定義されないということについて言及しておきます.というのも厳密な数学においては,まず「円周の長さ」を定義しなくてなりません.普通,弧長は定積分により定義されますが,円周の場合は三角関数の極限が必要になります.しかしその極限は円周の長さという幾何学的な説明で与えられるために循環してしまいますので,この循環を断ち切ることが求められます.
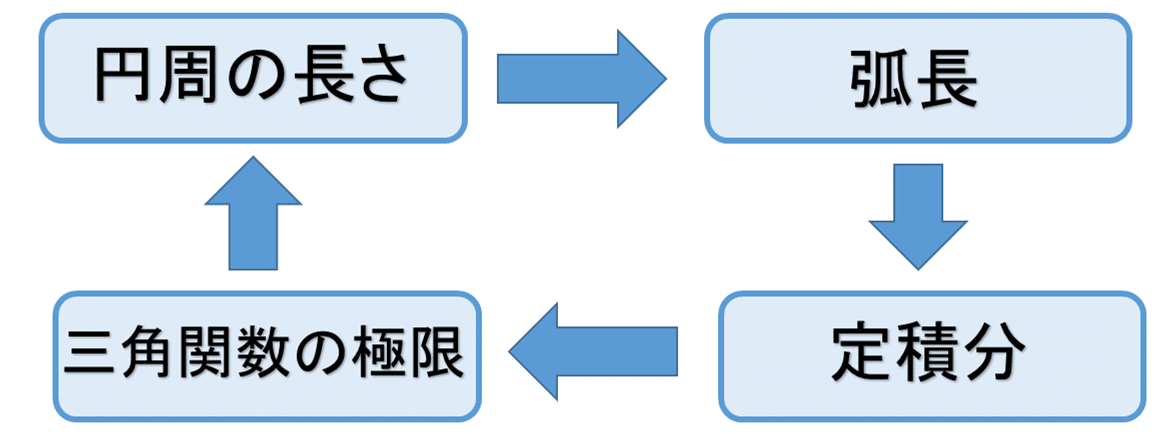
そこで,まず図形とは無関係に三角関数を無限級数で定義し,cosα=0 を満たす実数αが唯一つ存在することを証明します.そこで2α=πとなることを確認し,それを円周率と定義します.また,その円周率が円に内接する弧長の和の上限であることが示されることにより,伝統的な円周率の定義と現代数学の定義が一致することを確認することになります.図形に「量」を見出すことで発見された円周率は,パラダイム転換をへて図形とは無関係な実数として扱われることになりました.関心のある方は,杉浦光夫『解析入門Ⅰ』東京大学出版会(1980年)175-185頁,342-3頁 を参照してください.
文献紹介
注釈にないものを邦語文献に限り挙げておきます.
まず数学史一般に関心のある初学者の方に手頃なもの
・三浦伸夫『数学の歴史』放送大学教材,2019年が最良の入門書.
・佐々木力『数学史入門―微分積分学の成立』 ちくま学芸文庫,2005年 は数学の思想史的な内容が取り上げられています.
・吉成薫(訳)『リンド数学パピルス』朝倉出版,1985年
・三浦伸夫『古代エジプト数学問題集を解いてみる』NHK出版,2012年
・室井和夫『バビロニアの数学』東京大学出版会,2000年
・田村松平(編)『科学の名著 ギリシアの科学』中央公論社,1972年
・斎藤憲『アルキメデス「方法」の謎を解く』岩波書店,2014年
・辻茂『遠近法の発見』 現代企画室,1996年
・神崎繁『プラトンと反遠近法』新館社,1999年
・エミール・ノエル (辻雄一 訳)『数学の夜明け』森北出版,1997年
・佐々木力『科学革命の歴史構造 上』岩波書店,1985年
