素数発見アルゴリズム ｜ エラトステネスのふるいはどのくらい速いのか？

ある自然数以下の素数全てを求めるアルゴリズムの一つとして，エラトステネスのふるいと呼ばれるアルゴリズムがあります．このあと紹介する愚直なアルゴリズムよりも高速であることが知られていますが，実際にどのくらい早いのか？というものはあまり見かけません．今回はエラトステネスのふるいと愚直な計算方法の計算量を計算し，実際にどの程度のオーダーで速いのかということを見ていきます．

愚直な方法のオーダー

通常，ある自然数n以下の全ての素数を列挙するには，1からnの各自然数が素数であるかどうかを判定していけばよいです．それではn以下の自然数kが素数であることを確認するにはどうすればいいでしょうか？それは，kより小さい全ての自然数で割り切れるかを確認すれば良いです．この時の（最悪）計算量を計算してみましょう．ランダウの記号を用いて解析していきます．

自然数kが素数であるかを判定する時に最悪k-1回の割り算が必要になります（もし途中で割り切れる場合は素数ではないと判定してk-1回以下で終わる）．よって，全体としては，

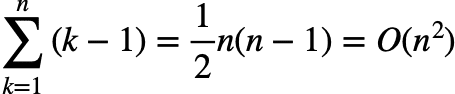
となり，２次のオーダーの計算量になります．

この愚直な方法は，簡単な考察で改善できます．それは

自然数kが√k以下の自然数で割り切れなければ，それより大きい数では割り切れない

という事実を用いることで実現します．

なぜならば，もしnが√k以下の自然数で割り切れないが，√kより大きい自然数mでnが割り切れたとします．またその商をqとします．すると，k = mqと書けます．この時，qは√kより小さい自然数でなければいけません．ところが，√k以下の自然数では割り切れないことに矛盾します．

よって，愚直な計算方法では，自然数kを1から√kまでの自然数で割り切れるかを確認し，割り切れなければ，素数であることを判定すればよいです．

よって最悪の場合の割り算の回数は，√k回程度であることがわかります．√k回程度をもうちょっと厳密にいうと，(√k - 1)回以上，√k回未満となります．よって，全体の計算量は，

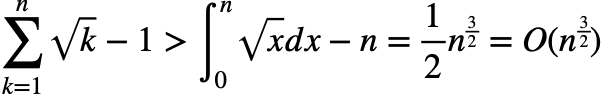
であることから，3/2乗のオーダーであることがわかる．積分による評価は，以下の図を見るとわかりやすいと思います．青い部分がシグマの和であり，赤い部分が積分になりますが，赤い部分より青い部分の方が大きくなります．また積分の部分に√nを足せば青い部分より大きくなります．

このオーダーよりもエラトステネスのふるいは速いと言われていますが，実際にオーダーとしてどの程度の速さなのかを確認していきます．

エラトステネスのふるいのオーダー

素数の逆数の和のオーダーがlog(log(n))である事実を使います．つまり，

ただし，P_nはn以下の素数の集合です．2乗の逆数は収束するので，素数も収束しそうな気がしますが，実際は発散します．余談ですが，この事実は素数の方が平方数よりも密に存在しているということを暗に示していることになります．

さて，エラトステネスのふるいのアルゴリズムをおさらいすると，

①残っている集合の中で，今まで最小値として選ばれていない最小値を取り出す．
②その最小値の倍数を消去する（最小値自身は消去しない）
③①に戻り，nまでいったら終わり．

実際にn=8で確かめてみます．
最初の集合は{2, 3, 4, 5, 6, 7, 8} です．

①残っている集合の中で最小値を取り出す．
これは2です．

②その最小値の倍数を消去する．
4, 6, 8が対象となり，残っている集合は{2, 3, 5, 7}となります．

①に戻り，nまでいったら終わり．
まだn=8まで行っていないので，①に戻ります．

最小値は，2ですが，すでに選ばれたことがあるので，次は3となります．
ただ今回は，3の倍数は残っていないので，消去される数はありません．

これを続けていくと，結局，{2, 3, 5, 7}が残り，それらは全て素数です．

結局，最小値として選ばれるのは，それより小さい数の倍数でないものなので，素数です．それをpとおくと，消去対象として選ぶ回数は，n/pとなります．これをnになるまで繰り返すので，計算量は，

となります．

従って，エラトステネスのふるいは，愚直なアルゴリズムより√nがloglognとなっている分，高速であることがわかります．