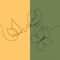フォトギャラリー用グラフ#5

この企画の目的：

• 毎日投稿のバッジ獲得のために、できるだけ楽をして記事を書く

• 「みんなのフォトギャラリー」で使える数学の画像を作る

• 図を見てるだけなら数学は思って貰えることを目指す

今回は指数関数$${y=e^x=\exp(x)}$$のべき級数展開に関するグラフです。画像の要点は、$${y=\sin(x)}$$のときと同じです。なお、$${y=\exp(x)}$$のべき級数展開は以下のようになります。

$$
\exp(x) =\sum_{n=0}^\infty\frac{1}{n!}x^n=1+x+\frac{1}{2!}x^2+\frac{1}{3!}x^3+\cdots
$$

指数関数$${\exp x}$$と三角関数$${\sin x}$$と$${\cos x}$$のべき級数展開から、オイラーの公式

$$
e^{ix} = \cos x + i\sin x
$$

が導かれます。ここから、小川洋子さんの『博士の愛した数式』で有名になった（らしい）

$$
e^{i\pi} + 1 = 0
$$

がでてきます。

---

以下は、グラフの描画に用いたPythonのコードです。Google Collaboratory で実行しました。

import matplotlib.pyplot as plt
import numpy as np

plt.rcParams['font.size'] = 10 # デフォルトの文字サイズ
r = 5.0
fig, ax = plt.subplots(figsize=(1.91*r,r))
W = 1.0 
x = np.linspace(-W,W, 100)
ax.plot(x, np.exp(x))
y = np.zeros(x.size)
for n in range(4):
  y = y + 1.0 / np.math.factorial(n) * x**n
  ax.plot(x,y)

plt.savefig("graph-20230608c.png",format="png",dpi=300)
plt.show()