標準偏差σ(X)(2)
前回(標準偏差 第1回)は以下より
該当ページ
数B 教科書 p.61
目標
標準偏差の深い理解
確率分布aX+bの分散、標準偏差を求める
ポイント
・標準偏差
→測定単位の次元が同じで、期待値からの散らばりを表す値。(前回の復習)
・確率変数aX+bの標準偏差
→後述の手順通りにやれば解ける
確率変数がどうなっても、公式を丸暗記せずに、手順通りに解くことをまずは優先する
(解き続けてたらだんだん覚えてくるから、覚えようとしなくていい)
aX+bの分散と標準偏差
a, bを定数とするとき、確率変数aX+bの分散と標準偏差を求める。
確率変数Xの期待値E(X)について
E(X)=m
とすると、
E(aX+b)=aE(X)+b=am+b
このとき、確率変数aX+bの分散V(aX+b)は、
確率変数{aX+b-(am+b)}^2の期待値であるから、
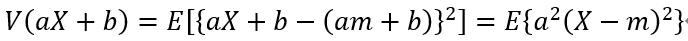
のように表される。
したがって、分散V(aX+b)と標準偏差σ(aX+b)は以下のようになる。


*細かい解説、式変形、考え方の過程は添付PDFの2ページ目を参照してください。ここで書くと、式だらけで長くなっちゃうので。
(例8)
1個のサイコロを投げて出る目をXとすると、
E(X)=7/2, V(X)=35/12, σ(X)=√105/6
このとき、
確率変数2X+1の期待値、分散、標準偏差は、

〈練習9〉
(例8)において、次の確率変数の期待値、分散、標準偏差を求めよ。
(1)X+4 (2)-2X (3)3X-2
以下、解答

次回
確率変数の和と積
この記事が気に入ったらサポートをしてみませんか?
