
科学と聖書にまつわる随想(21)
「変調と側波帯」
前記事(20)では、変調がかかるとスペクトラムが広がるということについて述べました。この点について、もう少し突っ込んで考えてみたいと思います。正弦波を搬送波(情報を運ぶ乗り物)とする場合、変調の方式としては、振幅変調、周波数変調、位相変調の3種類が考えられます。伝送したい情報を表す信号を変調信号と呼びますが、変調信号に応じて搬送波の振幅(振れ幅のことで、別の言い方をすれば強度とも言える)を変化させるのが振幅変調(AM : Amplitude Modulation)、周波数(1秒間に何回振動するか)を変化させるのが周波数変調(FM : Frequency Modulation)、タイミングのズレを変化させるのが位相変調です。このうち、周波数変調と位相変調については、もちろん違いはありますが、実は、本質的には同じものになります。
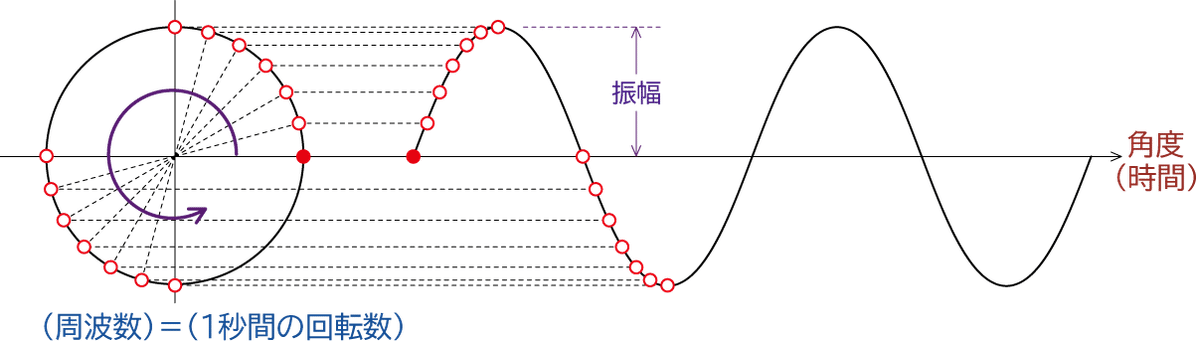
まず、純粋な正弦波は、図1のように、一定のスピードで回転する点に光を当ててできる影の動きとして表すことができます。この時、回転の半径が振幅、1秒間の回転数が周波数に当たります。また、一般に、回転の向きは反時計回りを+の向きと考えます。
また、図2のように、同じ回転速度で逆向きに回る2つの点を重ね合わせると、横向きの成分は常に互いに逆向きですので打ち消し合い、軸にそって正弦波的に往復して振動する点になります。正確に言うと、縦向きの成分は足し算になりますから、軸に沿った振動の振幅は2倍になりますが、分かりやすいようにそのままにして描いています。

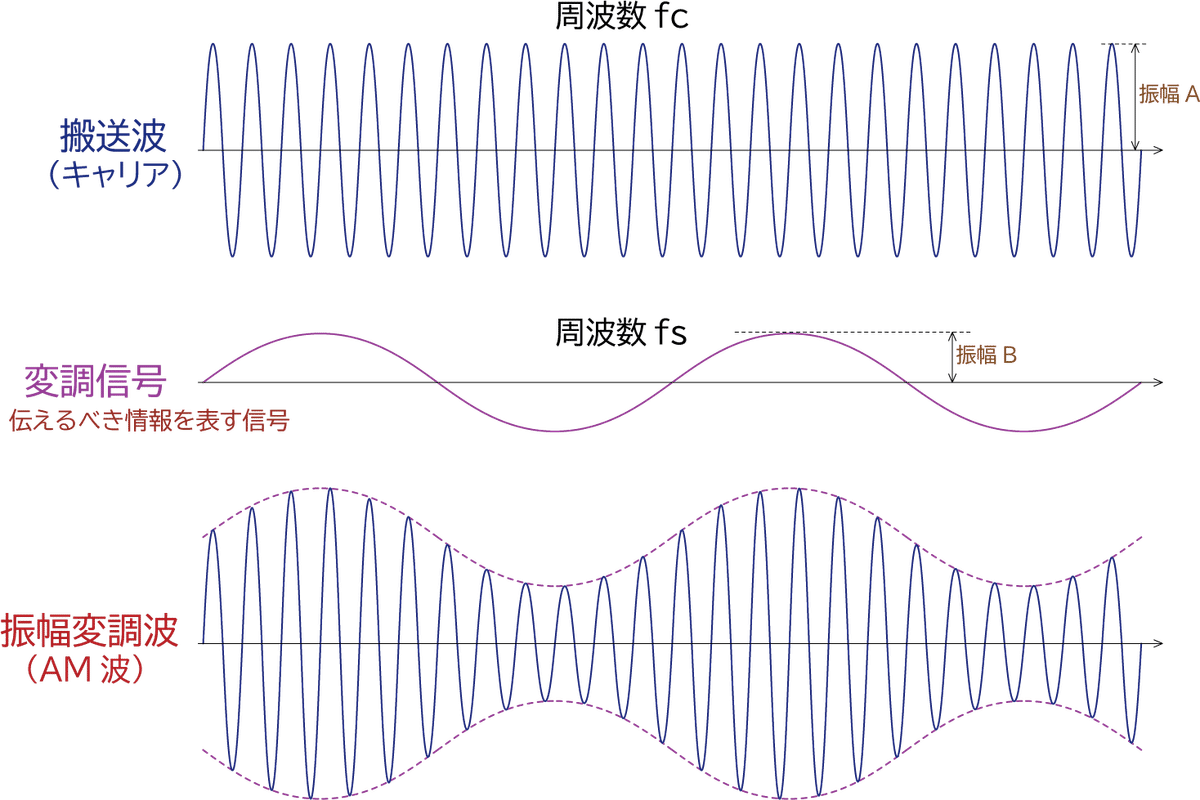
ところで、振幅変調をかけると波形がどのようになるのか考えてみましょう。図3をご覧ください。搬送波の周波数を fc とします。搬送波は正弦波で、fc は一般に非常に高い周波数です。周波数が高いということは、1秒間に山と谷がいっぱい詰まっているということですが、あまり沢山描くと絵がグチャっとなってしまいますので、図では山と谷の数はほどほどに描いてあります。これに対して、変調信号はずっと低い周波数で、fsとしましょう。例えば、中波帯のAMラジオの場合、fc は 550kHz~1600kHz で、変調信号は音声信号ですから、fs はせいぜい数kHzと考えてよいでしょう。つまり、fc は fs の100倍程度以上はあることになります。
振幅変調をかけるということは、搬送波の振幅(Aとします)を変調信号(振幅をBとします)に従って増減するということです。変調信号は +B と -B の間で振動していますから、搬送波の振幅が A+B から A-B の範囲で変化することになります。ですから、A>B であることが必要条件です。といっても、搬送波はアンテナから飛ばす電波の信号であって十分に強く、一方で変調信号はマイクで拾った弱い音声信号ですから、基本的に A>B の条件は満たされることになります。
振幅変調波の波形を、回転する点の動きで考えてみましょう。図4をご覧ください。搬送は周波数fc振幅Aの正弦波ですから、半径 A で1秒間に fc 回回転する点で表すことができます。ここで、自分もこれに付いて一緒に1秒間に fc 回グルグル回っていると考えてみてください。あるいは、紙面(画面?)も一緒に fc のスピードでグルグル回してみると考えてもよいでしょう。そうすると、この点はあるところで静止しているように見えるでしょう。ところで、振幅変調をかけて搬送波の振幅を、周波数 fs で A+B と A-B の間で変化させるということは、図2の理屈を適用すると、この静止して見えている点を中心として、左向きと右向きに1秒間に fs 回回転する2つの点の重ね合わせで表せることになります。今、自分は1秒間に fc 回左向きに回転しているので、外側の人の目から見ると、これら2つの点の一方は1秒間に fc+fs 回、もう一方は fc-fs 回回転していることになります。

これは、すなわち、周波数fcの搬送波を周波数 fs の変調信号で振幅変調すると、周波数が fc+fs の成分と fc-fs の成分が生まれる、ということを意味しています。これを図で表すと図5のようになります。このように、変調によって搬送波の上下に現れる成分を“側波帯(sideband)”と呼びます。実際の変調信号は一般には正弦波ではなく、いろいろな周波数の成分を含んでいるので、それぞれの成分がそれぞれの周波数の分だけ+/-の側波帯を作りますので、ある周波数の幅を持つことなり、このため“帯(band)”という表現が用いられます。

しかし、これは、よくよく考えてみれば不思議なことです。変化させたのは搬送波の振幅であって、周波数をいじくっている訳ではありません。周波数というのは1秒間の振動数ですから、波形で言えば1秒間の山と谷の数です。図3で、搬送波の波形と振幅変調波の波形を見比べてみてください。山と谷の数はどちらも同じです。つまり、周波数は同じです。にもかかわらず、これとは異なる周波数の成分が潜んでいるというのです。例えて言うならば、私が1秒間に5回のスピードで手を振っているとします。そして、その振り幅を1秒間に1回の割合で大きくしたり小さくしたりしたとします。そうすると、その時、私と共に、1秒間に6回手を振ってる私と、1秒間に4回手を振っている私が同居している、ということになるのです。これは、インマヌエル(神が共にいます)ということの原理を示唆しているようにも思います。聖書の御言葉よにって私たちの心が揺さぶられて変調を受けると、側波帯が生まれることになるのですが、それがすなわち共にいます神なのではないかと。図5で、搬送波のスペクトルの両側に側波帯のスペクトルが広がっている様子は、いかにも側波帯によって搬送波の脇が固められて守られているかのようです。
振幅を変調することで周波数まで変わってしまう、ということですが、周波数変調なら周波数が変わるのはなおのこと、ということは理解に難くないでしょう。周波数変調の場合は、側波帯の広がり方がさらに広くなります。ですので元の搬送波の周波数も、振幅変調の場合に比べてずっと高くしておく必要があります。FM放送の周波数がAM放送よりずっと高いのはこのためです。さらに実は、きちんとした説明のためには数学が必要になりますのでここでは割愛しますが、周波数変調波も、変化させているのは周波数なのですが、さまざまな振幅変調波の重ね合わせで表現することができるのです。実際のところ、今となっては使われませんが、昔の人はモノが無かったなりによく考えた一つの例として、アームストロング変調回路と呼ばれる回路があり、これは振幅変調回路を用いて周波数変調(または位相変調)を行うことができる回路です。また、最初に申しましたように、周波数変調と位相変調は違いはあれども本質的には同じものになります。
したがって、結局のところ、「振幅変調」「周波数変調」「位相変調」の3つは、表面上の区別と違いはありますが、その根本においては同一の源から出たもの、ということができるのです。これはまさしく、「父なる神」「イエス・キリスト」「聖霊」がその本質において同一である、という偉大な真理の写し鏡のようではないでしょうか。
イエス・キリストの言葉。
「わたしと父とは一つです。」
「父が持っておられるものはすべて、わたしのものです。ですからわたしは、御霊がわたしのものを受けて、あなたがたに伝えると言ったのです。」
「ですから、あなたがたは行って、あらゆる国の人々を弟子としなさい。父、子、聖霊の名において彼らにバプテスマを授け、わたしがあなたがたに命じておいた、すべてのことを守るように教えなさい。見よ。わたしは世の終わりまで、いつもあなたがたとともにいます。」
