
階層ベイズモデリングに挑戦
1. 想定したデータ取得環境
これまでは、一般化線形モデルを中心にベイズ統計モデリングを行ってきました。今回は一般化線形モデルでは当てはまらないモデルのデータ分析を行うために、階層ベイズモデリングに挑戦しました。
想定したデータ取得環境としては↓図をイメージしています。今回も自分が興味を抱いている運動と脳機能の研究計画をまねて理解の促進を図りました。
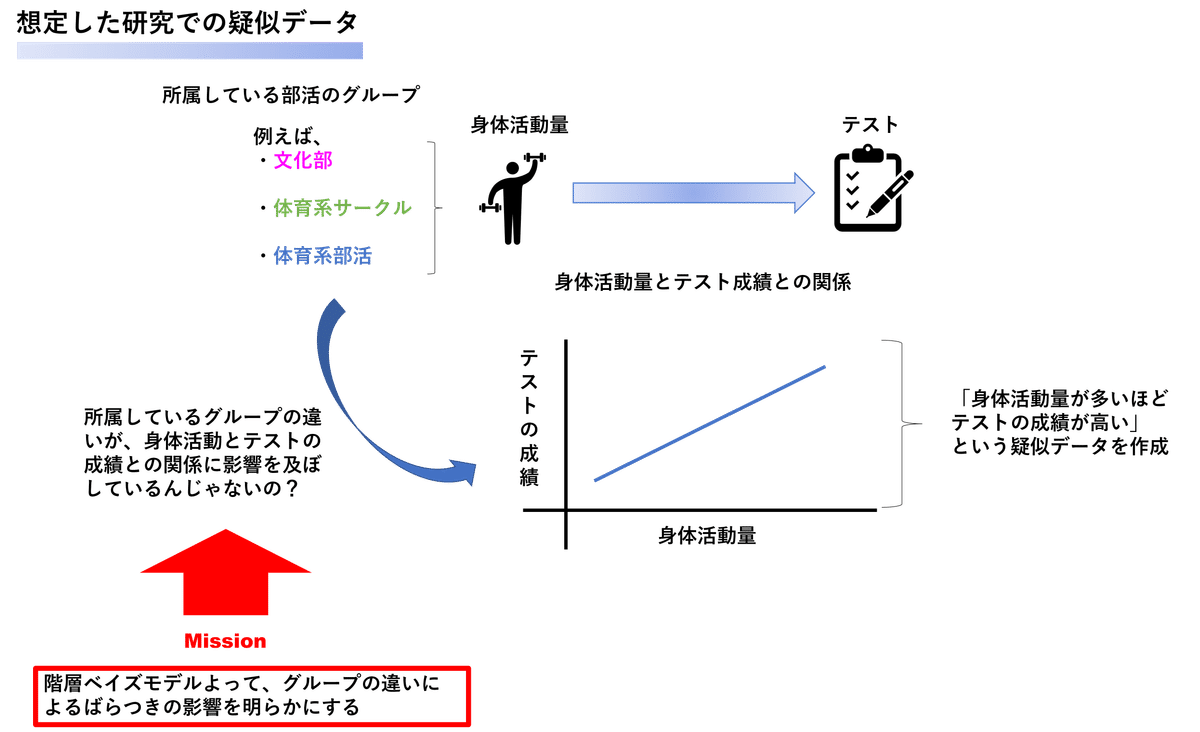
身体活動量とテストの点数との関係性に所属しているグループ(ここでは、部活の種類をイメージしました)の違いによるばらつきの影響を明らかにすることを目的に階層ベイズモデリングに取り組んでいきます。
2. データセットの作成
上記に示した設定での疑似データを乱数発生によって作成しました。乱数発生によって作成したコードは↓のようになっています。
####データセットの作成####
#スコアの乱数生成
ta=rnorm(100,50,5) #正規分布:平均50で標準偏差5の乱数
tb1=rnorm(50,65,5) #正規分布:平均65で標準偏差5の乱数
tb2=rnorm(50,65,5)
tc=rnorm(100,80,5) #正規分布:平均80で標準偏差5の乱数
#身体活動量の乱数生成
ea=rnorm(100,20,5) #正規分布:平均20で標準偏差5の乱数
eb1=rnorm(50,40,5) #正規分布:平均40で標準偏差5の乱数
eb2=rnorm(50,40,5) #正規分布:平均40で標準偏差5の乱数
ec=rnorm(100,60,5) #正規分布:平均60で標準偏差5の乱数
#グループの乱数生成
ga=as.integer(runif(100,min=1,max=3)) #整数:1~2で乱数生成
gb1=as.integer(runif(50,min=1,max=3)) #整数:1~2で乱数生成
gb2=as.integer(runif(50,min=2,max=4)) #整数:2~3で乱数生成
gc=as.integer(runif(100,min=2,max=4)) #整数:2~3で乱数生成
#データフレームの作成
data1=data.frame(ta,ea,as.factor(ga))
data2_1=data.frame(tb1,eb1,as.factor(gb1))
data2_2=data.frame(tb2,eb2,as.factor(gb2))
data3=data.frame(tc,ec,as.factor(gc))
#データフレームの列名変更
names(data1) <- c("score", "physical_activity","group")
names(data2_1) <- c("score", "physical_activity","group")
names(data2_2) <- c("score", "physical_activity","group")
names(data3) <- c("score", "physical_activity","group")
#データフレームの結合
data_all=rbind(data1,data2_1,data2_2,data3)データセットのコードに関する説明は↓の記事をご参照ください。
グラフに図示してみてどのようなデータになっているか確認してみます。

Y軸にテストの点数、X軸に身体活動量をとっています。所属しているグループごとに色を変えてプロットしています。グループについては、1が文化部、2が体育会系サークル、3が体育会系部活をイメージしています。そのため、1→3になるにしたがって身体活動量が多くなるようなデータセットとしています。
このグラフから分かることとしては、身体活動量が増えるほどテストの点数が高いことがわかります。この身体活動量とテストとの関係にグループ(文化部、体育会系サークル、体育会系部活)の違いによるばらつきの影響について明らかにすることを目的とします。
注意:本記事では乱数発生によってデータセットを作成しています。そのため、本記事での結果が一般的な現象の結果を表しているわけではございませんのでご注意ください。
3. モデル式
上記に示した関係を表すモデル式は↓のようにしました。

グループの違いにおけるランダムな効果を検証するということで、いわゆる一般化混合線形モデルの形となっています。この一般化線形モデルに階層ベイズモデリングを適用することによって、グループのばらつきの影響を明らかにしていきます。
モデル式に関する詳細は、本記事の参考文献・資料にあげた[2]・[3]・[4]をご参照ください。
4. 階層ベイズモデリングの適用
では、実際に階層ベイズモデリングを行っています。
Stanのコードは↓のようになりました。
data {
int N;
int G;
real Physical_activity[N];
real Score[N];
int<lower=1, upper=G> Group[N];
}
parameters {
real a0;
real b0;
real ag[G];
real bg[G];
real<lower=0> sig_a;
real<lower=0> sig_b;
real<lower=0> sig_Score;
}
transformed parameters {
real a[G];
real b[G];
for (g in 1:G) {
a[g] = a0 + ag[g];
b[g] = b0 + bg[g];
}
}
model {
for (g in 1:G) {
ag[g] ~ normal(0, sig_a);
bg[g] ~ normal(0, sig_b);
}
for (n in 1:N)
Score[n] ~ normal(a[Group[n]] + b[Group[n]]*Physical_activity[n], sig_Score);
}Stanで記載したコードをRにて実行していきます。
library(rstan)
rstan_options(auto_write = TRUE)
options(mc.cores = parallel::detectCores())
N = nrow(data_all)
G = 3
data_list = list(N=N, G=G, Physical_activity=data_all$physical_activity, Score=data_all$score, Group=as.numeric(data_all$group))
mcmc_r <- stan(file='hieralchy.stan', data=data_list, seed=1234)StantとRのコードに関する詳細は、本記事の参考文献・資料にあげた[1]・[2]・[3]・[4]をご参照ください。
事後分布の結果は↓のようになりました。

テストの点数におけるグループの違いによるばらつき(sig_a)をみると8.67であることが分かります。また、身体活動量に伴うテストの点数に関するグループの違いによるばらつきをみると0.183であることが分かります。
これらのことから、今回使用したデータセットでは、グループの違いによるばらつきの影響を考える必要があることがわかりました。一般化線形モデルではテストの点数と身体活動量の関係しかわかりませんでしたが、一般化混合線形モデルにおける階層ベイズモデリングを適用することで所属しているグループによるテストの点数のばらつきの影響を明らかにすることができました。
5. モデルの予測
最後に、得られた事後分布からデータの予測(95%信頼区間)を行ってみました。Group1から3の結果を↓の図に表しています。



予測された回帰における95%信頼区間にもとのデータが収まっていることがわかりました。階層ベイズモデリングを適用したことによって、本データセットにおいて、グループごとの身体活動量とテスト点数の関係を表すモデル式が立てれたのではないかと考えれます。
6. おわり
本日はここまでとします。これまでのの勉強によって、一般化線形モデルと一般化混合線形モデルをベイズ統計モデリングにおける事後分布から検証・予測することができるようになりました。たた、統計全般・ベイズ統計に関してはまだまだ勉強中の身ですので、データの記載や解釈等に間違いがありましたら、ぜひコメント等で教えてください。
この回をもってベイズ統計モデリングの勉強は一旦終了します。次はベイズ機械学習の勉強に移っていきます。引き続き、統計とベイズの勉強を行っていきます。
最後まで読んでいただきありがとうございました。
参考文献・資料
[1] 馬場真哉 (2019).「実践Data Scienceシリーズ RとStanではじめる ベイズ統計モデリングによるデータ分析入門」講談社
[2] 松浦健太郎 (2016).「StanとRでベイズ統計モデリング」共立出版
[3 ]線形混合モデルと階層ベイズモデルを使ったデータ解析の実践
https://www.medi-08-data-06.work/entry/stratified_model
[4] 階層ベイズモデルを使ったデータ解析の実践~より複雑なモデルへ~
https://www.medi-08-data-06.work/entry/stratified_model2_1901
