ベイズ統計モデリングへの挑戦～ロジスティック回帰分析～

2022年7月18日 21:20

　今回はベイズ統計モデリングのロジスティック回帰分析に挑戦して学んだことをまとめていきます。今回も、身体活動量に関する疑似データを乱数によって発生させて、そのデータをRとStanを用いてベイズ統計モデリングによるデータ解析を行っておいきます。

　今回のデータセットで想定した場面は↓の図のようになっています。

　ざっくり言うと、身体活動量と体格指数であるBMIがテストにどのように関わっているか明らかにしていきます。今回はテストにおける合格と不合格という2値を目的変数として、身体活動量とBMIを説明変数としていきます。ロジスティック回帰分析を行うことによって、身体活動量がどの程度増加する(もしくは減少する)と合格するオッズという寄与率を明らかにすることができます。つまり、合格へどれだけ近づけるのかという指標を得ることができます。

注意：本記事では乱数発生によってデータセットを作成しています。そのため、本記事での結果が一般的な現象の結果を表しているわけではございませんのでご注意ください。

データセットの作成

　乱数は発生によってデータセットを作成していきます。疑似データのデータセットは↓のコードによって作成しました。

setwd("～")#ワーキングディレクトリの設定
getwd()#ワーキングディレクトリの確認

####データセットの作成####
#1. スコアの乱数生成
ta=rnorm(100,50,5) #正規分布：平均50で標準偏差5の乱数
tb=rnorm(100,65,5) #正規分布：平均65で標準偏差5の乱数
tc=rnorm(100,80,5) #正規分布：平均80で標準偏差5の乱数
#身体活動量の乱数生成
ea=rnorm(100,20,5) #正規分布：平均20で標準偏差5の乱数
eb=rnorm(100,40,5) #正規分布：平均40で標準偏差5の乱数
ec=rnorm(100,60,5) #正規分布：平均60で標準偏差5の乱数
#2. BMIの乱数生成
ra=as.integer(runif(100,min=1,max=3))　#整数：1～2で乱数生成
rb=as.integer(runif(100,min=1,max=4))　#整数：1～3で乱数生成
rc=as.integer(runif(100,min=2,max=4))　#整数：2～3で乱数生成
#3. データフレームの作成
data1=data.frame(ta,ea,ra)　
data2=data.frame(tb,eb,rb)
data3=data.frame(tc,ec,rc)
#4. データフレームの列名変更
names(data1) <- c("score", "physical_activity","BMI")
names(data2) <- c("score", "physical_activity","BMI")
names(data3) <- c("score", "physical_activity","BMI")
#5. データフレームの結合
data12=rbind(data1,data2)
data_all=rbind(data12,data3)

#6. 合格の判別(60点以上が合格)
data_all$result=ifelse(data_all$score >= 60,1,0)

#7. BMIのラベル付け
trans <- function(x) { 
  BMI <- c("1"="痩せ", "2"="標準","3"="肥満")
  BMI[as.character(x)]
}
data_all[,3] <- trans(data_all[,3])

#8. BMIをダミー変数に変換
data_all$BMI1[data_all$BMI!="痩せ"]<- 0
data_all$BMI1[data_all$BMI=="痩せ"]<- 1
data_all$BMI2[data_all$BMI!="標準"]<- 0
data_all$BMI2[data_all$BMI=="標準"]<- 1

　少しだけコード(R言語)の説明をしていきます。1. スコアの乱数生成では、正規分布による乱数発生によってテストの点数と身体活動量のデータを作成しています。#2. BMIの乱数生成では、1～3の数字を用いてBMIのデータを作成しています。作成したBMIのデータは、#7. BMIのラベル付けにて、1→痩せ、2→標準、3→肥満としています。#3. データフレームの作成と#4. データフレームの列名変更と#5. データフレームの結合で乱数によって作成したデータを分析できる形にするためにデータフレームに格納しています。#6. 合格の判別(60点以上が合格)において、テストの点数が60点以上であれば合格(1を挿入)、60点未満であれば不合格(0を挿入)と判別する式を立てています。#7. BMIをダミー変数に変換において、BMIが痩せならば[1, 0]、標準ならば[0, 1]という数字が、データフレームに新たに作成したBMI1とBMI2の列に挿入されるように振り分けています。ここで、「あれ、BMIが肥満の人は？」と疑問を抱くかもしれません。一般化線形モデルによりモデル式を作成する場合に、カテゴライズされたデータはダミー変数を使用してモデルに使用します。ここで、ダミー変数を用いると、当初あった要因数から1を引いた要因数に変わります。ここでは3つの要因数(BMIが痩せ・標準・肥満)となっており、今回考える一般化線形モデルでは痩せと標準のデータを使用します。なお、今回のデータセットでは肥満については[0,0]で表される形となっています。

　実際にどのようなデータセットになったのか確認します。データセットの最初の20行と最後の20行をとりだしてみます。

#最初の20行の確認
head(data_all, n=20)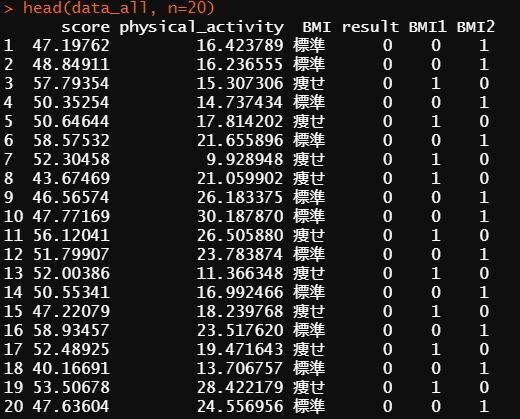

#最後の20行の確認
tail(data_all, n=20)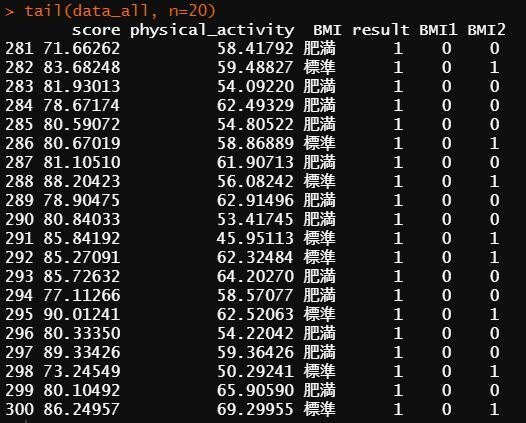

実際に想定したデータセットが作成できたことが確認できました。このデータセットを、y軸に合格・不合格(1:合格、0:不合格)とx軸に身体活動量として設定した図を描いていきます。

　身体活動量が高いほど合格する人数が増えていることが図から確認できます。また、合格者には標準や肥満のBMIの人が多いことが分かります。さて、この関係が本当に存在しているのかベイズ統計モデリングによるロジスティック回帰分析にて検証していきます。

2. ロジスティック回帰分析の実行

今回のデータセットでは目的変数が1か0かの2値ですので、ベルヌーイ分布による一般化線形モデルを作成していきます。
　モデル式は↓のようになります。
q[n]=inv_logit(切片＋β1×身体活動量[n]+β2×BMI痩せ[n]+β3×BMI標準[n])
Y[n]～Bernoulli(q[n])
となります。事後分布はStanを用いたMCMCにより作成します。上記のモデルをStanの機能であるBernoulli分布をロジットでパラメータ化するコードを使用して、Y[n]～bernoulli_logit(切片＋β1×身体活動量[n]+β2×BMI痩せ[n]+β3×BMI標準[n])のモデルからロジスティック回帰分析を行っていきます。

ロジスティック回帰分析なので、切片と言わずにβ0を使ったほうがいいですね。重回帰的なノリで回帰式を作成してしまいました。。。

　上記のモデルにMCMCを行うためのStanのコードを↓のように書きました。

data {
  int N;
  real physical_activity[N];
  int<lower=0, upper=1> BMI1[N];
  int<lower=0, upper=1> BMI2[N];
  int<lower=0, upper=1> result[N];
}

parameters {
  real Intercept;
  real b_physical;
  real b_BMI1;
  real b_BMI2;
}

model {
  for (i in 1:N)
    result[i] ~ bernoulli_logit(Intercept + b_physical*physical_activity[i] + b_BMI1*BMI1[i]+ b_BMI2*BMI2[i]);
}

Nはサンプル数とし、データは身体活動量・BMI痩せ・BMI標準を使っていきます。回帰モデルのパラメータには、切片とβ1～3に該当する項目を挿入しています。modelにベルヌーイ分布おける回帰式を入れています。
Stanのコードに関する詳細は、本記事の参考文献・資料にあげた[1]と[2]をご参照ください。

　上記のStanを実行するコードをRに書いていきます。

library(rstan)
rstan_options(auto_write = TRUE)
options(mc.cores = parallel::detectCores())
#mcmcの実行
sample_size=nrow(data_all)
data_list=list(N=sample_size, physical_activity=data_all$physical_activity,BMI1=data_all$BMI1, BMI2=data_all$BMI2,result=data_all$result)
mcmc=stan(file="ex_logistic.stan",data=data_list,seed=1)

　この箇所におけるコードの説明も、本記事の参考文献・資料にあげた[1]と[2]をご参照ください。

3. ロジスティック回帰分析の結果

MCMCによる事後分布の結果は↓のようになりました。

モデルの収束に関しては、Rhatが1となっており、トレースプロット(下図)からも確認できました。

各パラメータの事後平均の値から推定されたモデルは、
Y[i]～bernoulli_logit(-6.12＋0.20×身体活動量[n]-0.94×BMI痩せ[n]-0.66×BMI標準[n])となっていることが分かりました。このモデルから身体活動量が増加すると合格へ近づくことが考えられます。また、BMI痩せとBMI標準は負の関連を示していることから、BMIは肥満であるほうが合格には近づきそうです。ただし、95%信頼区間を見てみると、 BMI痩せは[-2.32, 0.39]、BMI標準は[-2.00, 0.62]と0をまたいでいることから、負の関連を示しているとは必ずしも考えづらそうです。ベイズ統計における信頼区間の見方は直観的で解釈しやすいですね。
　これらのことから、テスト合格にには身体活動量の増加が重要となりそうなことが分かりました。オッズ比をみてみて、目的変数である合格への効果の程度を確認してみます。
　例えば、身体活動量が50の人と40の人のオッズ比を比べると、
exp(2.0×50)/exp(2.0×40) = exp(2.0×(50-40))=7.389
となり、オッズ比の推定値は7倍違うことが分かりました。

データからモデルを考えて、RとStanを用いてベイズ統計モデリングによるデータ解析を行うのは楽しいですね。

本日はここまでとします。最後まで読んでいただきありがとうございました。統計全般・ベイズ統計に関してはまだまだ勉強中の身ですので、データの記載や解釈等に間違いがありましたら、ぜひコメント等で教えてください。

参考文献・資料
[1] 馬場真哉　(2019)．「実践Data Scienceシリーズ RとStanではじめるベイズ統計モデリングによるデータ分析入門」講談社
[2] 松浦健太郎 (2016)．「StanとRでベイズ統計モデリング」共立出版
[3] 日本統計学会 (2020)．「日本統計学会公式認定統計検定準1級対応統計学実践ワークブック」学術図書出版社
[4] R ダミー変数を使用した回帰分析？　https://jojoshin.hatenablog.com/entry/2016/05/08/005747