
インドラの真珠:ショットキー・ダンス
前節のショットキー円では、変換を繰り返していくときどんなことが起こっているのでしょうか、詳しく見てみましょう。
リンク先を開くと,次の図が表示されます。右にボタンをスライダがあります。ボタンが表示されていない場合は再読み込みしてください。

2つの円と円周上の3点の対応でメビウス変換とその逆変換を定義し、これを2組、全部で4つの変換を作りました。上の図で、円AとB、CとDが組になっています。4つの変換による円Aの像を見てみましょう。円Aを選んで、A->Bの対応で作ったメビウス変換「A->Bの変換」を行うと、円Bに写ります。赤で表示されるのが円Aの像です。円Bに重なるので円Bの色が変わっていますね。

「A->Bの変換」 のボタンをもう一度クリックして解除し,今度は「A->Bの逆変換」を行うとAの内部に写ります。

次にC->Dの対応で作ったメビウス変換「C->Dの変換」を行うと、円Dの内部に写ります。

次に「C->D」の逆変換を行うと、円Cの内部に写ります。
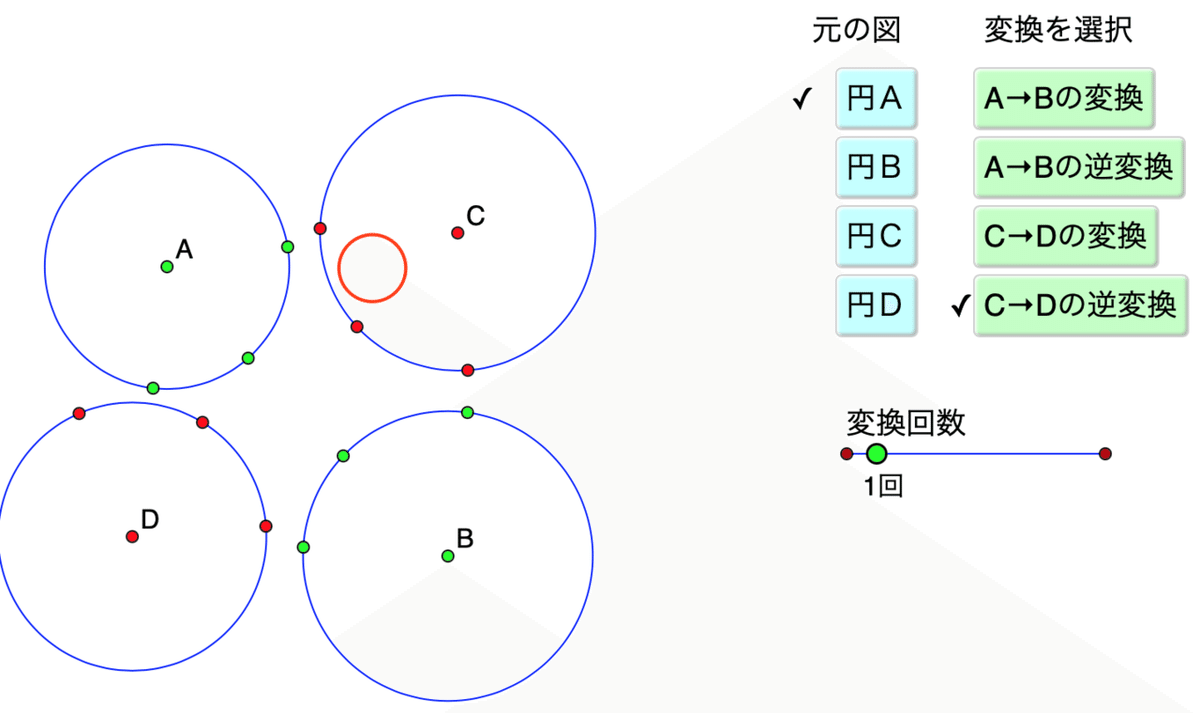
4つともやってみましょう。

円Aのボタンをクリックして解除し,円Bを選んでみましょう。

ボタンを全部選んでみましょう。それぞれの円の内部に3つずつ小さな円ができます。

こんどは,反復回数を増やすとどうなるかを見てみましょう。「円A」と「A→Bの変換」ボタンだけ残し,他は解除します。
回数のスライダを動かして,2回にしましょう。

回数は4回までです。円はどんどん小さくなるので4回まででよいことにしました。では,すべてのボタンをチェックし,回数を増やしてみましょう。回数を増やすと描画に時間がかかって反応が鈍くなりますので,先に回数を増やしてからボタンをチェックするほうがよいでしょう。

小さな円がチェーン状になっています。
円の中心,円周,対応させる円周上の点をドラッグして図を変えてみましょう。そのままだと反応が遅いので,いったん,変換ボタンを解除してから点をドラッグし,その後変換ボタンをチェックするようにしましょう。
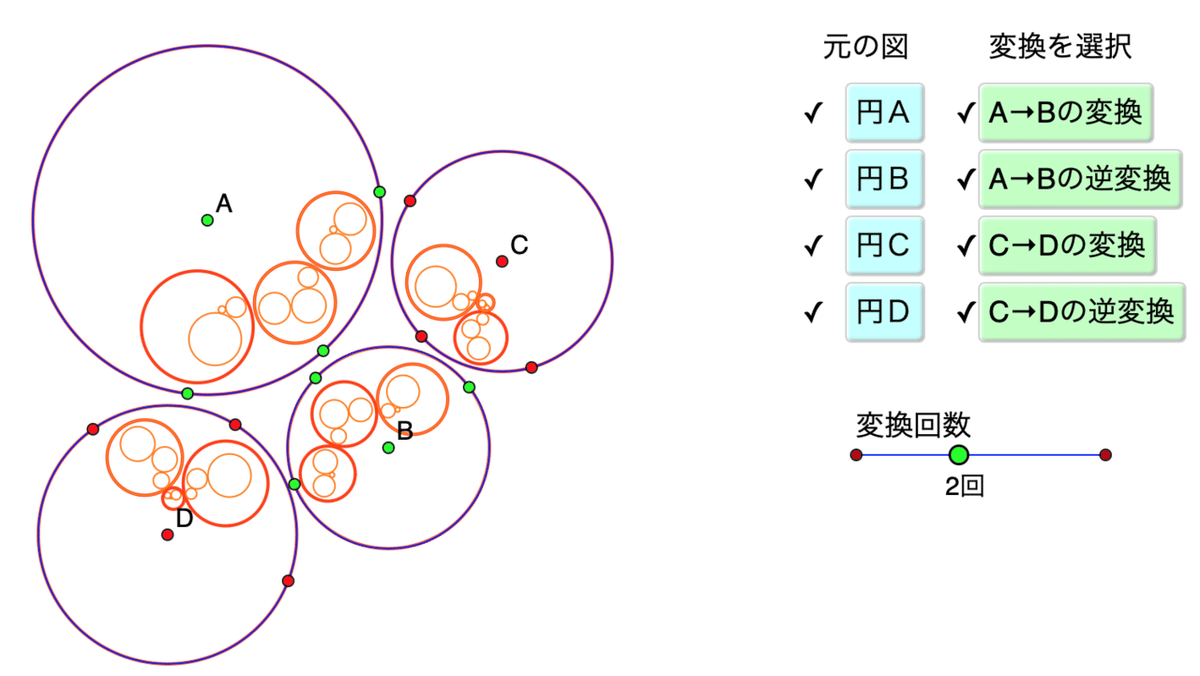
前の節で,4つの円を、変換の定義に用いている一つの点でちょうど接するようにすると、小円のチェーンがつながって閉じた曲線になると書きました。しかし、そのようにうまく接するようにするのはなかなか大変です。
そこで、2円の中心を結ぶ線上に点がくるようにしたのが次です。
リンク先を開くとつぎの画面になります。今度は円が塗られています。

先ほど,すべての円とすべての変換を選んだときの図です。ただし,4つの変換のうち3つずつで写しています。たとえば,円Aをまるまる円Bに写す変換はおこなわず,内部に写るものだけです。
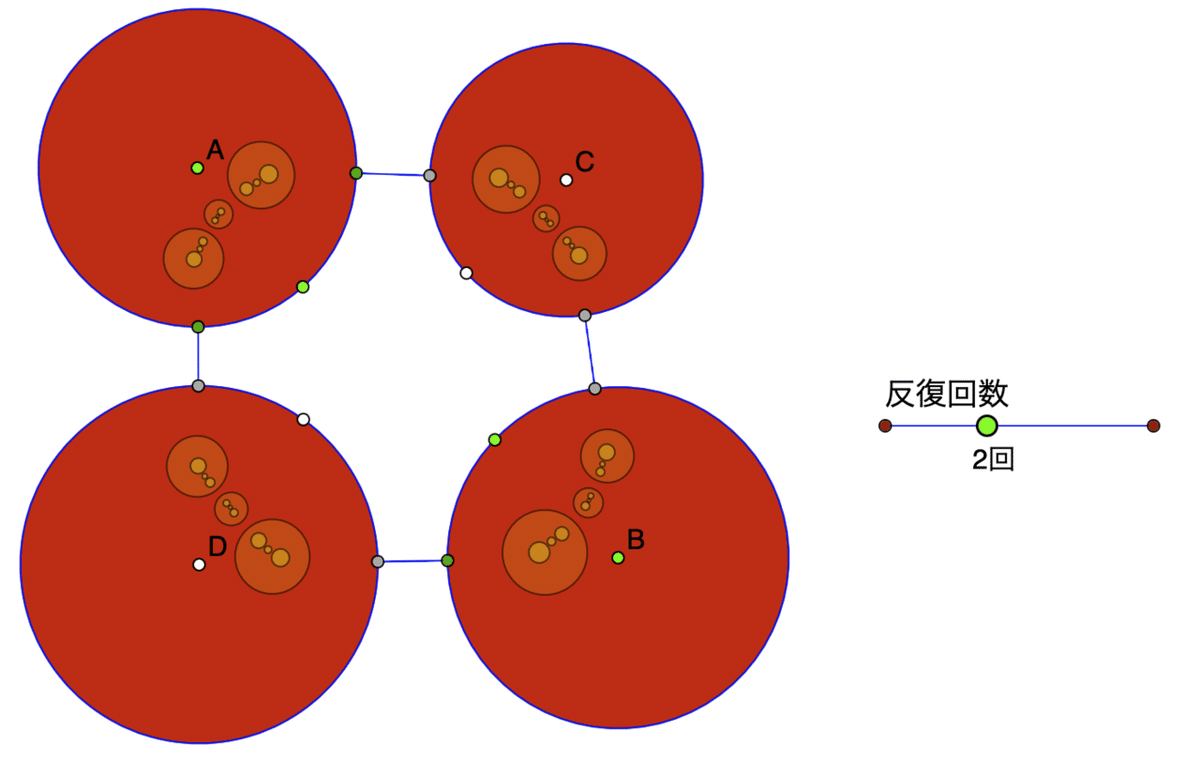
メビウス変換を定義するための3点のうち,2組ずつが細い線で結ばれていますが、これは2円の中心を結ぶ線上にあります。
円の位置や大きさを変えてみましょう。反復回数を増やすと美しい図ができるでしょう。

ところで,タイトルの「ショットキー・ダンス」ですが,何が「ダンス」なのか,「インドラの真珠:マンフォード他著 小森洋平訳:日本評論社」には,次のように書かれています。
2つの(メビウス)変換は実にさまざまな方法で相互作用するので、これはとても興味深い問題です。2つの変換はお互い最善を尽くしてダンスをしようとがんばるのですが,いつもうまく踊れるとは限りません。 <91ページ>
上の図は,93ページに示されているのと同じような図ですが配色が異なります。配色も93ページの図に似せて作ったのが次のリンク先にあるものです。

さらに,101ページには,次のような図があります。それぞれの円の像がどのように写っていくかを色分けしています。

円Aは黄色で,その像も黄色です。たとえば,円Aの,A→Bの逆変換での像は円Aの内部になりますので,円Aの中に黄色の円があります。
反復回数を増やし,円の大きさや位置も変えてみましょう。

→次節:ショットキーの極限集合
→インドラの真珠:目次 に戻る
