
学び直しの算数:かけ算
小学校で「かけ算」というと,よく話題になるのが順序問題です。note にもいくつか書かれています。たとえば,
その他にもいろいろありますが,中には学習指導要領などに対する誤った認識があるものや,根拠が「小学校の」を逸脱しているものもあります。立ち位置が異なる人が議論すると物別れに終わります。毎年11月ごろにTwitterなどで起きている現象です。
ここでは,「学び直しの算数」ですから,是非論ではなく,小学校でどのような順序でかけ算が教えられているかについて,教科書を参照しながら考えることにします。目標は分数のかけ算です。
なお,本稿はかなりの分量になります。目次を見て,適当に読みすすめてください。まとめを先に読んでも構いません。
かけ算の意味と九九
「かけ算」をはじめに学ぶのは2年生の10月ころで,たとえば学校図書の教科書では,遊園地のコーヒーカップの絵を載せて,「3人ずつ6台分で18人乗っている」としています。
また,ゴーカートの例を使ってかけ算の「×」という記号を導入しています。

さらに抽象的に次のように書いています。

これは,学習指導要領解説にある「一つ分の大きさの幾つ分かに当たる大きさ」に対応しています。
そのあと,九九に入ります。わかりやすい5の段,2の段から始め,「九九を覚えましょう」となるわけです。
つまり,
まずかけ算の意味を教え(定義し),1から9までの数についてのかけ算の結果を覚える
という学習順序です。
教科書がそのようになっており,「九九を覚える」がかけ算の基本と思われているため,まずは「九九の暗記」をすることになります。ところが,中学生になっても九九が言えない子がでてきます。それは暗記をしているからであって,暗記したものはたいてい忘れるものだからです。「九九を覚える」と「九九を暗記する」は異なるものです。これについては,次の記事を参照してください。
さて,学校図書の教科書では,節末にある次の練習問題をやるあたりから「かけ算の順序問題」が発生します。

この問題の意図は,
2+2+2+2 を 2×4 と表すのだから イ が正解(それが自然な考え方)
ということでしょう。前述の学習指導要領の用語でいえば,「一つ分の大きさが(一つのかごに)2で4つ分のとき2×4と表す」と考えたからです。
では,逆に「4つのかごにみかんが2つずつはいっているとき,みかんはぜんぶでなんこありますか」を式にして計算しなさい,という問題だったらどうでしょう。
2×4=8 が正解で,4×2=8 は間違いでしょうか。これが,「かけ算の順序問題」です。上の問題にしても,「ぜんぶの数を,みかんをとり出して数える」とすれば,「かごからまとめて出す」なら(ア)は4×2で(イ)は2×4,「ひとつずつ4回出す」なら(ア)は2×4で(イ)は4×2 となります。
はじめに書いた通り,本稿ではかけ算の順序問題を論じることはしませんので,これ以上の言及は避けますが,次の事実だけは紹介しておきましょう。
学習指導要領解説には,つぎの記述があります。
例えば,「1皿に5個ずつ入ったみかんの4皿分の個数」を求めることについて式で表現することを考える。「5個のまとまり」の4皿分を加法で表現する場合,5+5+5+5と表現することができる。また,各々の皿から1個ずつ数えると,1回の操作で4個数えることができ,全てのみかんを数えるために5回の操作が必要であることから,4+4+4+4+4という表現も可能ではある。しかし,5個のまとまりをそのまま書き表す方が自然である。そこで,「1皿に5個ずつ入ったみかんの4皿分の個数」を乗法を用いて表そうとして,一つ分の大きさである5を先に書く場合5× 4と表す。
つまり,「5+5+5+5の方が自然で,そのときは5×4と表す」としているわけで,「4×5は誤り」とは書かれていないのです。
かけ算の性質
かけ算は可換(交換法則:2×3も3×2も同じ)であることや,結合法則が成り立つこと((2×3)×4 と 2×(3×2)は同じ)は3年生の始め(4月)に学びます。また,かけ算のきまりとして,次のような性質を学びます。


これは,次の「0のかけ算」「10のかけ算」の準備になります。
0,10のかけ算
海外では,九九をこえて12×12やそれ以上を「覚える」国もありますが,日本では,九九の次に0,10のかけ算を考えた後,だんだん拡張していきます。
まず,0のかけ算です。たとえば 0×4 は 0+0+0+0 と考えればよいのですが,4×0はどうしましょうか。「一つ分の大きさの幾つ分」ですので,「一つ分が4で,0個分だから0」でしょうか。それでよいのですが,ここにはちっとした落とし穴があります。それは,わり算を考えるときです。a÷b のわり算を「aこのものをbずつに分ける」と考えると,0÷4 は「0個のものを4ずつに分けるけどもともと0個だから答えも0」となりますが,4÷0を「4個のものを0個にわける,つまりわけないのだから答えは0」としてしまいそうです。しかしそれは間違いで,「0個に分けるというのは,結局分けないのだからわり算の意味がない,つまり答えはない」と考えるのが正しいのです。言い方を変えると「0で割る演算は定義できない」となります。
0のかけ算にもどりましょう。学校図書の教科書では次のようにしています。「かけ算のきまり」を使うのです。得点ゲームで次の例を考えます。

ここで,ななみさんの考え方は,もともとのかけ算の意味「一つ分の大きさの幾つ分」を使っていることになります。だいきくんの考え方はこの少しあとに出てきます。

②は,「一つ分の大きさの幾つ分」ではなく,前述のかけ算のきまり①を使っています。③はそのまえのだいきくんの考え方をしましょうということです。②のように,こんどは「かけられる数が減っていく」場合を考えるのですが,かけ算のきまり②(交換法則)を使ってもよいでしょう。
つぎに,10のかけ算です。たとえば,5×10 を 5+5+5+5+5+5+5+5+5+5 ,10×5を10+10+10+10+10 とするのではなく次のように考えます。

どうでしょうか。わかりにくかったでしょうか。ここでつまづく児童が出ることが予想されますね。「かけ算のきまりを使う」ところでつまづくわけです。これは次の「かけ算の筆算」に移行するためのステップになっているのですが,単に「5が10個たして50」でよいのではないかと思います。
1桁の数をかける筆算
かけ算の筆算は3年生の9月に学びます。まず,20×4 や 200×4 といったかけ算を調べておきます。一の位が0の2桁の数,一と十の位が0の3けたの数です。
次に,一般的な2桁と1桁の数のかけ算を考えます。
たとえば,23×3 の場合,23を20と3に分け,3×3=9 と 20×3=60 を足します。それを次のような書き方をする,ということで筆算の書式が導入されます。

繰り上がりのあるかけ算は,一の位の結果と十の位の結果を2行に分けてつぎのように書きます。

3桁かける1桁も同様にすすめます。
2桁をかける筆算
2桁をかける筆算は3年生の1月ころに学びます。
学校図書の教科書では,次の問題を例としています。

計算式は 4×30 ですが,それをどう計算するか。次の2つの考え方を示しています。

そして次のようにまとめています。右の図で,ゆいさんの考えに基づいていることがわかります。

さて,このやりかた,何かひっかかるところはありませんか。すんなりと受け入れられましたか。
もう一度問題文を読んでください。「1枚の台紙にシールが4まい」台紙が「30まい」です。4×30なのですから,次の図を思い浮かべませんか。

台紙には縦に4つ横に10個のシールがはってあるのではなく,「4枚のシール」なのですから,教科書のように10枚ずつ途中で折り返すのでなく,横にずらっと並べるのが自然でしょう。そして,30枚ですから10+10+10で30枚です。すると,
4×10+4×10+4×10=40×3 という計算式も成り立ちますね。
10枚で折り返して 4×3 ×10=12×10 とするのは,はたして自然な発想でしょうか。
次の例題です。

左の計算手順は,40と30を分解し,かける順序を変えて(右の見方・考え方)計算をします。しかし,これを右の図で説明しようとするとそう簡単ではないでしょう。「12が100個で12×100」というのがすんなり理解されるでしょうか。
教科書では,この結果を次のようにまとめます。

先ほどの問題と合わせて「進め方」を見ると,次のようになっていることがわかるでしょう。
① いろいろな考え方で計算してみる
② どのようにやっても同じ結果になる
③ その中からひとつを取り上げ,「10倍だから右に0を1つつける」「100倍だから右に0を2つつける」という方法を「まとめ」として覚えるようにする。
この結果の③は,このあと2桁×2桁の筆算で使うことになります。

なお,青の矢印と説明文は筆者が追加したものです。実際には230の0は省略しますね。このあと,省略するようになります。
3桁かける2桁も同様にやっていきます。
面積
長方形の面積はかけ算で求めます。面積を学ぶのは4年生です。まず,「1辺が$${1cm}$$ の正方形の面積を$${1cm^2}$$と書く」ことを学びます。次に,辺の長さが整数の長方形を,縦横の線で区切って,1辺が$${1cm}$$ の正方形がいくつあるかを数えるのですが,これがかけ算でできる,というわけです。
「1辺が$${1cm}$$ の正方形がいくつあるか」つまり個数を数えるのです。すると,辺の長さが整数でないときにはどうなるでしょう。小数や分数は「個数」のイメージとかけ離れているので,同じようにかけ算でいいということに抵抗がありそうです。かけ算は「一つ分の大きさの幾つ分かに当たる大きさ」でした。「幾つ」は個数なので,小数で表された個数は考えにくいでしょう。この問題は,次の6年生の分数のかけ算のところで出てきます。
整数と小数のかけ算
小数のかけ算は5年生の6月ころに学びます。
例として,「1mあたり80円のリボンを2.4m買うときの値段」を考えます。それまでに,「比例」や「単位あたりのおおきさ」を学んでいるので,これを使って考えます。

右側の「見方・考え方」と「まとめ」を見てみましょう。
「見方・考え方」で「小数のときも整数のときと同じようにできるのかな」と問うています。これは,前述のように,かけ算は「一つ分の大きさの幾つ分かに当たる大きさ」としているからです。「幾つ」は整数というイメージですから。それに対して,ここで「いくつ分にあたる数が小数であっても」整数と同じようにできることを確かめているわけです。「なぜ同じようにしてよいのか」については書かれていません。授業をどのように進めれば,この「なぜ」に答えられるのでしょうか。
その次に,このような考え方も示しています。

ひろとさんの考え方は「単位を0.1mにする」と考えればいいわけですが,もし,「1mあたり85円」だったらどうするのでしょう。8.5 ×24 になってしまいますね。ななみさんの方は整数のかけ算とわり算になるのでよさそうですが,図には分数の$${\dfrac{1}{10}}$$ が書かれているのに,式は 24÷10 になっていて統一がとれていません。もちろん,「10で割るが$${\dfrac{1}{10}}$$ で,$${\dfrac{1}{10}}$$ =0.1」ということはすでに学んではいます。
「まとめ」の文章も「小数を整数になおして」をどのようにして整数になおすのかについては書かれていませんので,この「まとめ」だけを覚えても実際には計算ができないでしょう。
ここを理解するには,「小数とは何か」がわかっていないといけないわけですが,では,小数はどのように導入されているのでしょうか。
小数は3年生で学びます。水のかさを使って次のように導入します。

「1を10等分する」のです。この時点では分数を学んでいないので,「10分の1」という表現は使えません。なぜ10等分なのかの説明もしません。10進法だからなのですが,「進法」の概念は学んでいないからです。ともかく,「1より小さくで10個で1になる量」とするのです。したがって,先ほどの例でいうと,ひろとさんのように,「0.1mを基準にする」というのがよさそうです。もちろん,どちらの考え方でもできればそれに越したことはありません。
このように,小数のかけ算をどのように授業するかは簡単ではなく,教師の力量によることになります。
なお,「小数を整数になおして」は,このあとの縦書きの筆算に関係します。ご承知の通り,小数の筆算では,整数と同じように計算をして,小数の位置だけを考えるからです。
小数と小数のかけ算
整数と小数のかけ算に続いて,小数かける小数を考えます。

この文章題は,立式そのものが簡単ではないでしょう。2.1×2.3 でいい,と即座に答えられる児童はそれほど多くないのではないかと思われます。①の図を見ると,「比例」を使うということがわかります。しかし,「比例の考え方を使う」とは書かれていません。比例はこの少し前に学ぶのですが,整数しか扱っていないからでしょうか。「2倍,3倍」はやりますが「2.3倍」はやらないからです。しかし,概念としては比例そのものです。
計算のしかたは2通り示していますが,ななみさんの考えがこのあとの縦書きの筆算につながります。

整数と分数のかけ算
分数のかけ算は6年生で学びます。まずは,分数かける整数です。
例題は,「1dLあたり$${\dfrac{4}{5} m^2}$$ ぬれるペンキ3dLで何$${m^2}$$ ぬれるか」です。$${\dfrac{4}{5} \times 3}$$ という式はすぐに立つでしょうから,その計算方法が問題です。
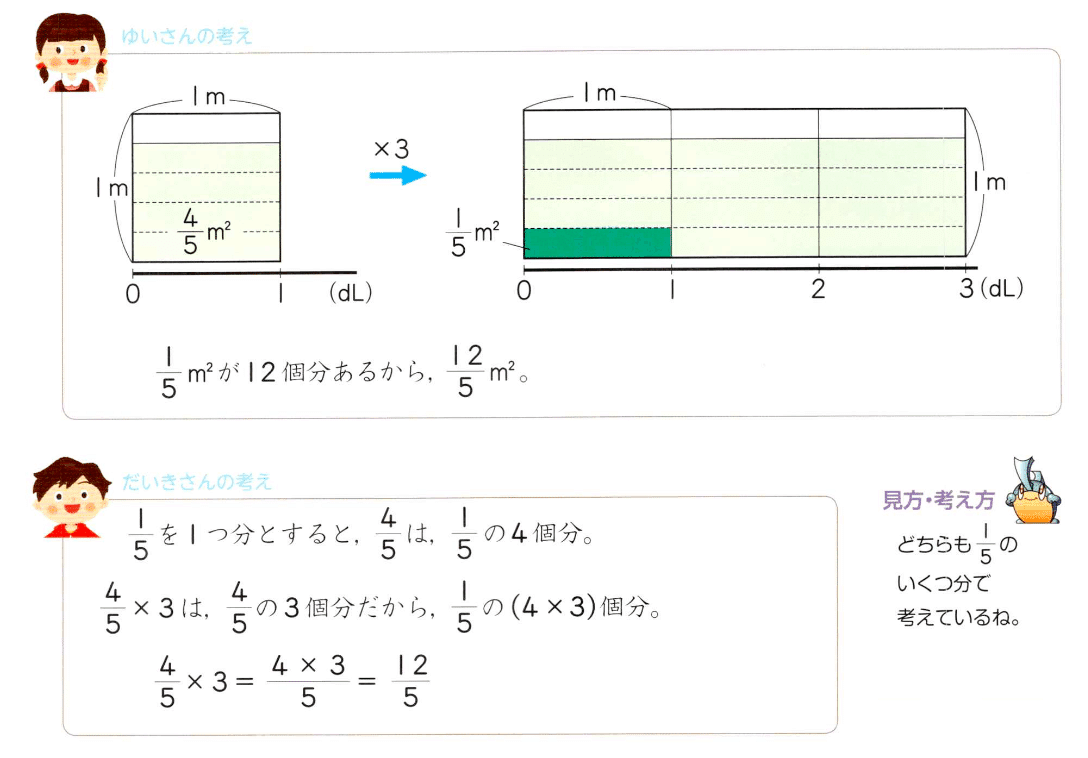
どちらも$${\dfrac{1}{5}}$$ をもとにして計算していますが,計算の進め方としてこのあとだいきさんの方法を採用します。すなわち,「分子にかける」です。
このあと帯分数と整数のかけざんが出てきますが,帯分数は仮分数にしてからかけることになります。
分数かける分数の計算
整数と分数のかけ算の次は,分数と分数のかけ算です。
例として,1dLあたり$${\dfrac{4}{5} m^2}$$ぬれるペンキで,まず $${\dfrac{1}{3}}$$mLを使ってぬれる面積を考えます。これが $${\dfrac{4}{5} \times \dfrac{1}{3}}$$ で求められることがわかるというのが最初のハードルですが,いままでの流れから「かけざんでいい」ということにしましょう。そこで計算のしかたを次のように図で考えます。

つぎに,おなじペンキを$${\dfrac{2}{3}}$$mL 使ってぬります。式は $${\dfrac{4}{5} \times \dfrac{2}{3}}$$ で,同じように図をつかって考えます。

ほかにも,前の結果を使ったり,$${\dfrac{4}{5} \times \dfrac{2}{3}=\dfrac{4}{5} \times \left( \dfrac{2}{3} \times 3\right)\div 3}$$ とする方法も考えた後,次のようにまとめます。

以後はこれを覚えて使っていくことになるわけです。
分数のかけ算の立式の問題
先ほどのペンキの例は,$${\dfrac{b}{a} \times \dfrac{d}{c}=\dfrac{b \times d}{a \times c}}$$ という計算方法を導くための例題です。いったんこの方法を学んだら,もとの文章がなくても同じような分数の計算をこれでやっていくのです。
では,少しもどって,「ハードル」と書いた,立式のところを考えます。
立式のところには次の図があります。

5年生で学ぶ「単位量あたりの大きさ」と比例の考え方を使って「かけ算でできる」とするのですが,この意味がわかるかどうかです。上の線分図と表の意味がわかりますか。わからなければ,この文章題からかけ算の立式をすることができません。しかし,かけ算の立式ができなくてもこの問題に答えることはできます。
教科書では,このあとに,面積の問題があります。

4年生で学んだ長方形の面積では,「1辺が$${1cm}$$ の正方形がいくつあるか」で個数を数えました。同じように,ここでは,縦横に分割した1つ分の面積を求め,それがいくつあるかを数えています。かけ算は「一つ分の大きさの幾つ分かに当たる大きさ」ですが,「幾つ分」が整数であれば,かけることに抵抗はないでしょう。
先ほどの問題にもどりましょう。
1dLあたり$${\dfrac{4}{5} m^2}$$ぬれるペンキを $${\dfrac{2}{3}}$$mLを使ってぬれる面積を求める問題です。これをかけ算で求められることに抵抗があっても,図を描いて(再掲)小さな長方形の数を数えればいいわけです。
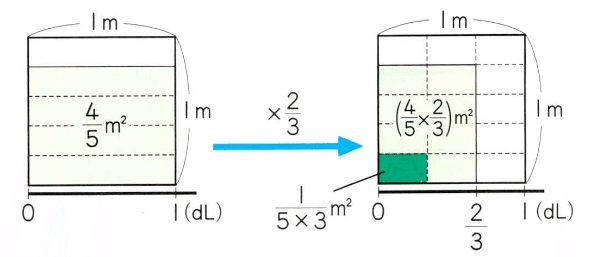
1辺1mの正方形を,縦5,横3に区切れば,一つ分は$${1cm^2}$$の15分の1。すると薄い緑の面積はそれが12個なので $${\dfrac{1}{15} \times 12}$$で求められます。個数は整数なのでをかけることに抵抗はないでしょう。$${\dfrac{4}{5} \times \dfrac{2}{3}}$$ の立式がされていなくても,このような説明があって計算が正しいなら正解とすべきですね。
まとめ
かけ算の導入から,分数のかけ算までの流れを整理しておきます。スタートは2年生です。
1. かけ算は「一つ分の大きさの幾つ分かに当たる大きさ」で,「×」記号で表す。
ここで,「幾つ」は個数なので,整数というイメージがある。整数でなくてもよいことは5,6年で学ぶ。
2. 1から9までのかけ算の結果がすぐ出せるようにする(2年生:九九)
ここで大切なのは「すぐ出せるようにする」ことです。覚えてしまえばすぐ出せますが,暗記することだけに頼ってしまうといずれ破綻します。暗記したものは大概忘れるということに留意しておくべきです。
3. 縦書きの筆算の方法を学ぶ(3年生)
2桁以上のかけ算は筆算で行います。
4. 整数のかけ算について交換法則や結合法則,その他の性質を学ぶ(3年生)
これらの性質はかけ算の計算を進めるときに使います。
5. 長方形の面積はかけ算で求められることを学ぶ(4年生)
長方形の面積とかけ算の関係は,5,6年で小数・分数のかけ算を,面積を題材にして導入するときに役立ちます。
6. 単位量あたり大きさや比例についての概念を学ぶ(5年生)
これは,小数,分数のかけ算を学ぶときの考え方につながります。「単位量あたりの大きさ」については別稿としました。
7. 小数のかけ算,分数のかけ算を学ぶ(5, 6年)
面積の問題を題材として小数・分数のかけ算を導入します。その結果,小数のかけ算や分数のかけ算の計算方法を覚えて,それを計算に適用していきます。分数でいえば「分子どうし,分母どうしをかける」という計算方法です。
以上の流れで押さえておくべきなのは次のことです。
① まず,新しい計算方法が必要な場面設定をする。
② 計算式の立て方を決める。
③ 計算方法を考える。
④ 計算手順について成り立つ性質を考える。
⑤ 他の場面でも同じ立式,計算ができることを確かめる。
これを,はじめは整数について行い,次に小数,次に分数と進めていくのです。
