
学び直しの算数:九九を忘れたら
はじめに
たとえば,「7×8=」と聞かれて,「しちは」までは出たけどその次が「いくつだっけ」となることはありませんか。筆者は結構あります。とはいえ,もちろんそのあとすぐに答えは出せます。どうやって出すかというと,「しちしちしじゅうく」は特徴的なので覚えています。7×7=49 がわかれば 7×8 もわかりますね。頭の中には次のイメージがあります。
45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58 ,・・・
・→7つ右 → → →・・ ↑
この図がわからないという人は,残念ながら数の順序と小学校2年生でのかけ算の意味がまったく理解できていないのです。教科書には,上の図とは違いますが,おなじことをやっている例題があります。

高校生になって九九が言えない生徒がいるというのは,今に始まったことではありません。「九九は暗記するものだ」とよくいわれます。塾の講師などでも,そういう人がいます。たぶん,小学校の教員でも多いでしょう。しかし,ただ暗記したものはたいてい忘れます。九九も,「しちは・・」を無意味に暗記したのでは,忘れたらもうどうにもなりません。
正しくは「九九は覚えるものだ」です。何度も使っている,あるいは「しちは・・」という語呂を言っているうちに覚えるのです。そして,そのときに,数の構造のうち,順序数をしっかり理解しておくのがよいのです。どうということはありません。1から81まで順にいえればいいのです。そして,「7×8 は 7 を8個足す」ということがわかっていればいいのです。
暗記したものは忘れる,だから九九は暗記しない,というのが,本稿のテーマです。
数の順序性(順序数)
小学校1年生のはじめに,10までの数を学びます。ものを数えて,数字で表します。どんぐりのようなものなら「こ」,さかななら「ひき」,とりなら「わ」です。
10までの数が書けるようになると,数を並べます。このとき「こ」や「ひき」はなくなります。「個数」から,抽象化した「数」になるのです。どんぐりの数を比較するときは「多い・少ない」ですが,数をならべたときは「大きい・小さい」になります。
この抽象化は,そう簡単に認知できるものではないと思うのですが,教科書ではなんの説明もなくおこなわれています。もちろん,小学校1年生の児童に「ちゅうしょうか」などといってもわかりません。わかっておくべきは教師です。ここをていねいに指導するかどうかで,その後の理解度が変わってくると思われるからです。ただし,多くの児童は,あまり疑うこともなく教えられた通りにできるでしょう。したがって,児童が数の概念をどのようにとらえているかは,そう簡単にはわかりません。あるとき気がつくのです。それは,数直線を扱ったときにわかります。
教科書では,「10まで」「20まで」「100よりちょっと大きい数まで」「1000まで」といった順で,小学校1年生から小学校2年生にかけて学びます。間に時刻や図形などをいれているのですが,これを「スパイラル方式」というようです。筆者は「分断している」と思うのですが。「10まで」はいいのですが,そのあとは20までといわず,100まで行けばよいのです。早めに数を順序数として(数はずっと並べることができる)認識できるようにするとよいのです。それは,将来,中学での負の数,高校での実数の概念につながっていきます。
小学校2年生でのかけ算の意味と九九
小学校2年生でのかけ算の導入は次のようになっています。

教科書には用語としては書かれていませんが,ここで2つの用語が使われます。
ひとつは,「かける数・かけられる数」もうひとつは「ひとつ分といくつ分」。上の例でいうと
・かける数は5,かけられる数は2です。
・ひとつ分は2,いくつ分は5です。図で,「2こずつ5はこ分」と書かれているところです。
ですから,かけ算は「ひとつ分×いくつ分」で式を立て「2×5=」とします。ここが,「かけ算順序問題」の中核なのですが,今はそのテーマではありません。いずれ稿を起こします。
教科書では,このようにかけ算の意味を学んだあと,九九を段ごとに調べていきます。段の順序は1,2,3・・ ではなく,2,5,3,・・・ ですが,この順序はたいした問題ではありません。わかりやすい順ということでしょう。それぞれ結果を数え,九九の語呂で覚えていきます。つまり,一度結果がわかったらあとは語呂で暗記しよう,というのです。この語呂は,日本独特のものですが,大変便利です。しかし,その一方,冒頭でも述べたように,忘れてしまったらどうにもならない,という脆弱性もあるのです。そのため,前述のように,教科書にも「忘れたら」という例題があります。この例題は大切なのですが,単なる例として素通りされてしまいそうです。
教科書では,かなりのページ数を使ってかけ算を学びます。九九がひととおりすむまでおよそ30ページあります。(学校図書の教科書の場合)そのあとに,さらにかけ算の性質などを学びます。かける数とかけられる数を入れ替えても結果は同じであること(可換)も次のように学びます。

ここで使っているブロックの図は,左右で並び方が違っていますから変に思う児童もいるかもしれません。3×5の図は,3が横に5つ並んでいます。5×3の図は5が縦に並んでいますね。しかし,この図は,面積を表す図と考えることができるのです。面積を学ぶのは4年生ですが,そこにつながります。面積の計算は,たて×横でも、横×たてでもよい,ということにもつながっています。これらは,いずれ,かけ算の順序問題にかかわってきます。
ここでは次のことをまとめとしておきます。
・かけ算の導入に,「かける数・かけられる数」「ひとつ分といくつ分」という用語があること。
・九九の語呂にはかけ算の意味は含まれていないこと。
・かけ算は可換であること
小学校3年生以降のかけ算
小学校3年生以降,かけ算は次のように扱われます。
・3年生 0をかける,10をかける,筆算。
・4年生 面積とその計算,小数×整数。
・5年生 整数×小数,小数×小数,分数×整数,体積
・6年生 分数のかけ算
このうち,面積,小数のかけ算,分数のかけ算は,その理解のしかたとともにいろいろな話題を含むものですが,それについては別に稿を起こします。
ここでは,2年生で九九(の語呂)を学び,それが以降の数の学びの基礎になること,九九は無意味に暗記するものではないということを頭に入れておきましょう。
順序数を用いた九九の練習
教科書の,「段ごとに結果を計算して覚える」,あるいは九九の表で覚えるというのとは少し違う方法を,次のnoteに書きました。
ここで紹介されている練習ツールでは,九九の表ではなく,次の表を用いて練習します。

この表は,数を並べると同時に,10進法による位取り記数法もわかるようにしています。しかし,数直線のように数を直線上に並べたものを使うのもよいだろうということで,そのような練習ドリルを作りました。
問題画面は次のようになっています。

画面にある数の中には答えはありませんから,→ボタンで並び方を動かします。「ひんと」ボタンを押すと,答えの候補が出ます。
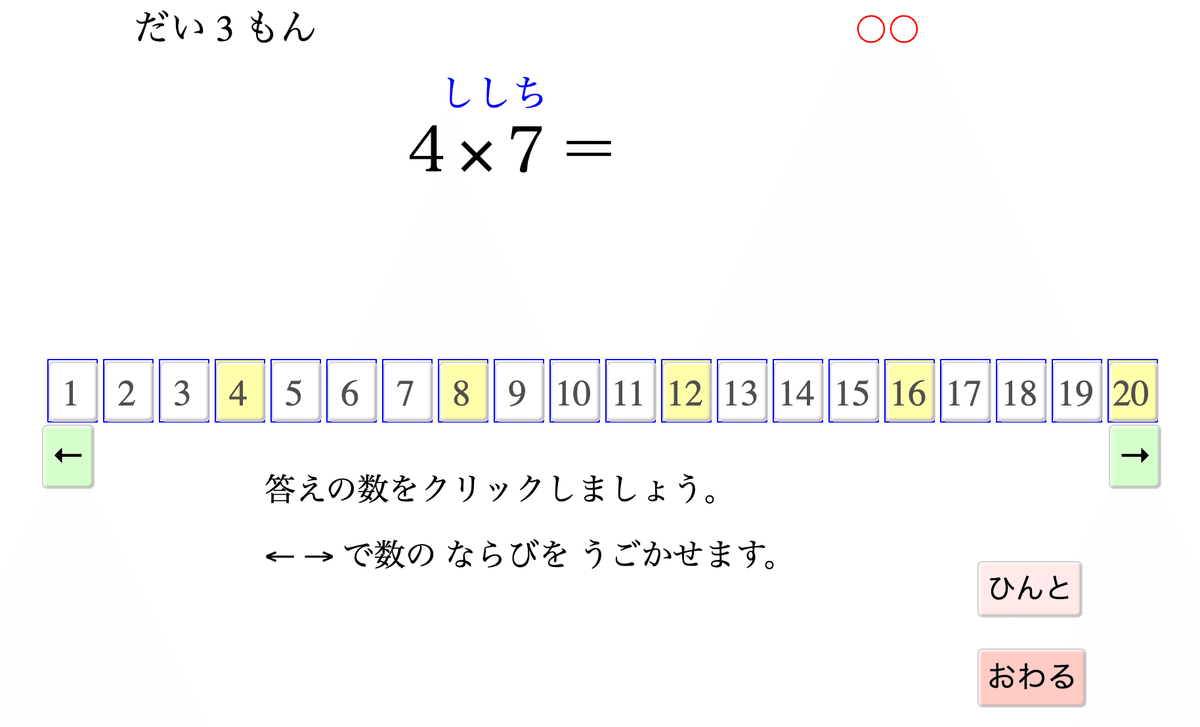
答えの数をクリックすれば正誤の判断が行われます。

ひんとボタンを押さずに,答えればもちろんよいのですが,どちらかというとはじめのうちはひんとボタンを押して欲しいのです。4の倍数が並んでいる,というイメージを頭の中に持ちたいからです。
