
インドラの真珠:複素関数(2)
複素関数によって複素平面上の点はどのように写されるか。こんどは1つの点だけではなく、図形でみてみます。
リンク先を開くと次の画面になります。ボタンが表示されていない場合は再読み込みしてください。

関数は6種類。係数は$${a,\ c,\ d}$$の3つで,$${a}$$ は実数です。スライダを動かすと変えることができます。煩雑にならないように小数点以下第2位を四捨五入します。$${c,\ d}$$ は複素数です。初期状態は$${c=1+4i , \ d=-2+i}$$ ですが,平面上でドラッグして変えることができます。こちらも煩雑にならないように,実部,虚部とも小数点以下第2位を四捨五入します。
もとの値は$${z}$$ で赤い点,関数で写った点が青い点です。赤い点のまわりにグリッド(方眼)があります。$${z}$$を中心にしてグリッドが描いてあります。「グリッドを写す」ボタンをクリックすると,方眼の像ができます。

「グリッドを写す」ボタンをもう一度クリックすると点だけに戻ります。
初期状態の関数は $${f(z)=e^{az}}$$です。係数は$${a=1}$$ なので,$${f(z)=e^{z}}$$ ですが,eのz乗とはどのような関数なのかを考えておきましょう。はじめは$${z=1}$$ なので関数の値は$${e}$$ です。青い点の値が $${2.7183}$$ となっています。ネピア定数$${e}$$ の値ですね(小数点以下第4位まで表示)。では,$${z}$$ が1でない場合はどうなるでしょうか。
基本になるのは、オイラーの公式
$${e^{i \theta}=\cos \theta + i \sin \theta}$$
です。「複素数の累乗」で示したように、これは絶対値が1で偏角がθの複素数です。なお,このオイラーの公式の導き方はここでは触れません。
これを用いて、eのz乗は次のように考えることができます。
$${e^z=e^{x+iy}=e^x e^{iy}=e^x(\cos y +i\sin y)}$$
ここで指数法則を用いていますが、複素関数でも指数法則は成り立ちます。(証明はパスします)赤い点をドラッグして,$${z=1+i}$$ にしてみましょう。$${z^{1+i}=e(\cos 1+i \sin 1}=1.4687+2.2874i}$$ となります。
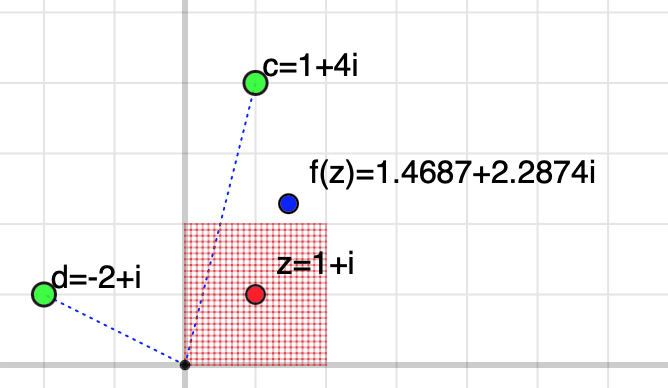
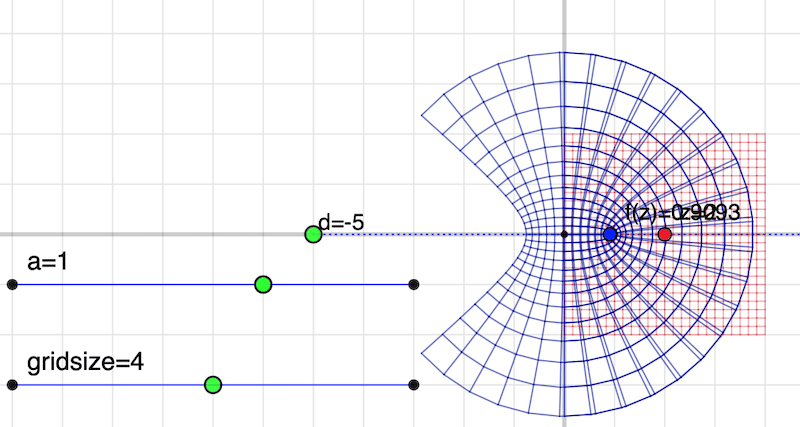
$${z=1}$$ に戻して,「グリッドを写す」ボタンをクリックしましょう。格子点全部を写すことになります。面白いのは,$${z=2}$$ や $${z=-1}$$ とすると,扇型が拡大・縮小することです。

$${z=1+i}$$ にすると次のようになります。

$${z=0}$$ にしてグリッドのサイズを大きくすると,原点中心のクモの巣状になります。

他の関数も見てみましょう。$${f(z)=az}$$など は「複素関数(1)」にもありました(下図左)。$${f(z)=z^2}$$ は下図右のようなきれいな図になります。

「複素関数(1) 」になかったのが$${\sin(az),\ \cos(az)}$$ です。
複素数の三角関数は次のように定義します。
$${e^{i \theta}=\cos \theta+i \sin\theta}$$
$${e^{-i \theta}=\cos \theta-i \sin\theta}$$
から,
$${\cos \theta = \dfrac{e^{i \theta}+e^{-i \theta}}{2},\sin \theta = \dfrac{e^{i \theta}-e^{-i \theta}}{2i}}$$
ここで,$${\theta}$$ を $${z}$$ として,複素数の三角関数を次のように定義します。
$${\cos z = \dfrac{e^{iz}+e^{-iz}}{2},\sin z = \dfrac{e^{iz}-e^{-iz}}{2i}}$$
次の図は$${f(z)=\sin(az)}$$ で,$${z=2}$$ としたものです。グリッドサイズを変えるとグリッドの像が変化します。
面白いのでいろいろ実験してみましょう。
→インドラの真珠:目次 に戻る
