
Cinderellaで数学:2次関数と他の関数との合成
三角関数との合成
$${f(x)=\sin x}$$ の $${x}$$ を、2次関数$${x^2}$$ にしたり、逆に2次関数$${f(x)=x^2}$$ の $${x}$$ を、$${\sin x}$$ にしたりします。このような関数を合成関数といいます。前者は$${g(x)=\sin x^2}$$, 後者は $${g(x)=\sin ^2 x}$$となります。
$${\sin ^2 x}$$ に関する問題は,たとえば
方程式 $${2 \sin ^2 x-\sin x -1=0}$$ を解け
というものがあります。このときはグラフは使わず,$${\sin x =t}$$ とおいて,まず2次方程式 $${2t^2-t-1=0}$$ を,$${-1 \leqq t \leqq 1}$$ であることに注意して解けばいいわけですし,教科書でも参考書でもそうなっています。この方程式は数学Ⅱで出てくるので,$${f(x)=2 \sin ^2 x-\sin x -1}$$を微分して増減表を書いてグラフを描く,ということはできません。微分はわからなくても,Cinderella で,どんなグラフになるかは表示できるのでその姿を見ておくのもよいのではないでしょうか。
plot(2*sin(x)^2 - sin(x) - 1);
でグラフは描けます。数字の表示などは適宜。
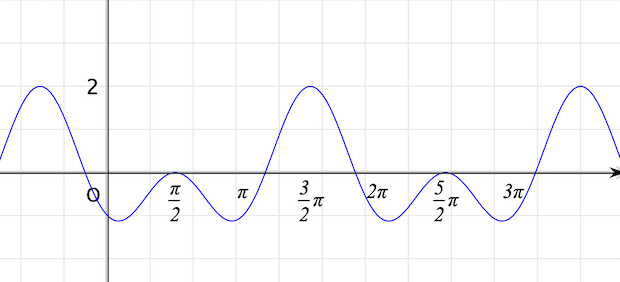
ところで,$${\sin x^2}$$ と $${\sin ^2 x}$$ は異なるものですが,上の関数で$${f(x)=2 \sin x^2-\sin x -1}$$ と2乗の位置を間違えるとどうなるでしょうか。それがタイトル画面のグラフです。こういうのもやってみると面白いでしょう。
指数関数との合成
三角関数と同様、方程式 $${4^x-2^{x+1}=0}$$ を解くような問題が数学Ⅱにでてきます。指数法則を使って $${(2^x)^2-2 \cdot 2^x=0}$$ と変形できるので,
$${2^x=t}$$ とおけば2次方程式です。これもグラフは使いませんが,面白いのでグラフを描いてみましょう。
その前に、2つの関数 $${y=2^x}$$ と $${y=x^2-2x}$$ から,これを合成した $${f(x)=(2^x)^2-2 \cdot 2^x}$$ のグラフが想像できるでしょうか。

$${y=2^x}$$ の左の方から値を追っていくと,0に近い値からだんだん大きくなっていきます。それも,次第に急激になっていきます。
これを $${y=x^2-2x}$$ のグラフで追って行くと、0に近いところから減少し、やがて増加に転じていきます。$${f(x)=4^x-2^{x+1}=0}$$のグラフは次のようになります。

分数関数との合成
関数 $${f(x)=\dfrac{1}{x^2+1}}$$ は、2次関数 $${y=x^2+1}$$ と分数関数 $${y=\dfrac{1}{x}}$$ の合成で、シンプルな形をしています。グラフは y 軸に関して対称な次のような曲線です。この曲線には、「アーネシの魔女」という魅力的な名前がついています。

また、$${0 \leqq x \leqq 1}$$ の範囲で、曲線と $${x}$$ 軸で挟まれる部分の面積は $${\dfrac{\pi}{4}}$$ というきれいな数になります。面積は定積分で計算しますが、もっとも基本的な置換積分の例です。
このように,「微分して増減表を書いて」ということをしなくても関数のグラフを見ることができるのは,単に「問題を解く」「解き方を覚える」というのではない数学の学習になります。
