静岡県高校入試2023年度数学第6問
2023年度の静岡県高校入試の数学第6問は,2次関数のグラフを使った問題です。問題文全体はWebを参照して下さい。静岡県高校入試 2023 で検索すれば出てきます。たとえば,東進のページにPDFがあります。
その第6問の(2)は,「RさんとSさんは,タブレット型端末を使いながら,図のグラフについて話している。」という設定です。タブレット端末上で図を動かして考えるのです。このような設定は,2022年度以前にはありません。大学入試共通テストで似たような設定が出てきたので,それに倣っているのではないかと思われます。
図形の問題を動的に見るということはとても大切なことで,その感覚はパソコン・タブレット端末などで動かしてみることによって養われます。
そこで,ここでは Cinderella(CindyJS) を使ってこの問題を見てみましょう。
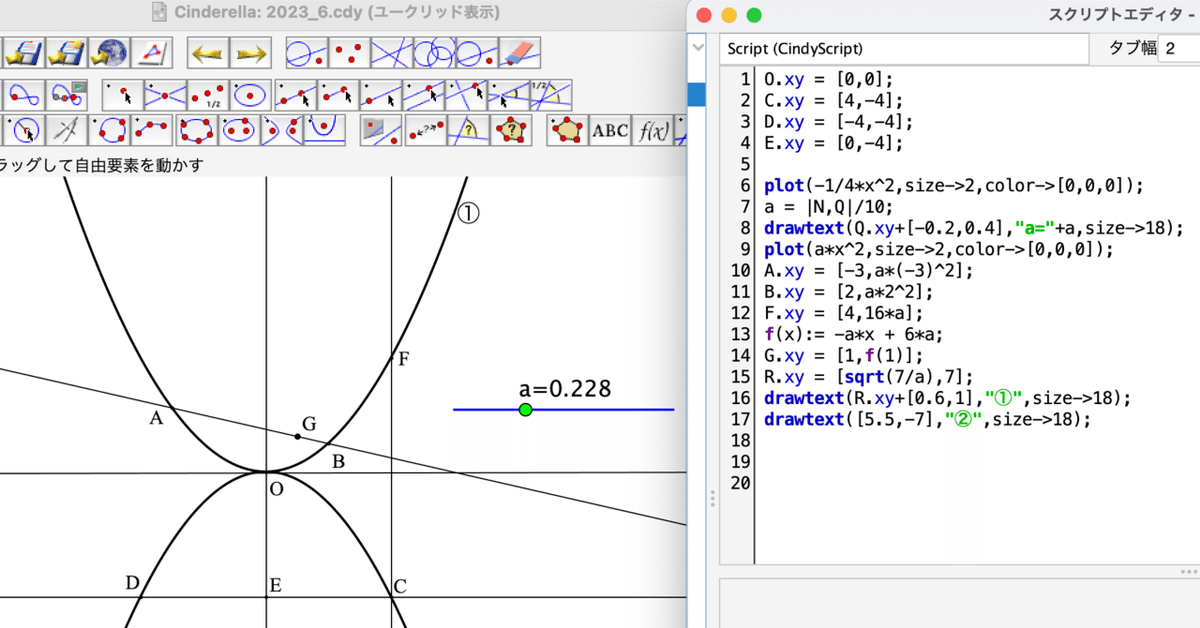
リンクを開くと問題図になります。2つの放物線があります。
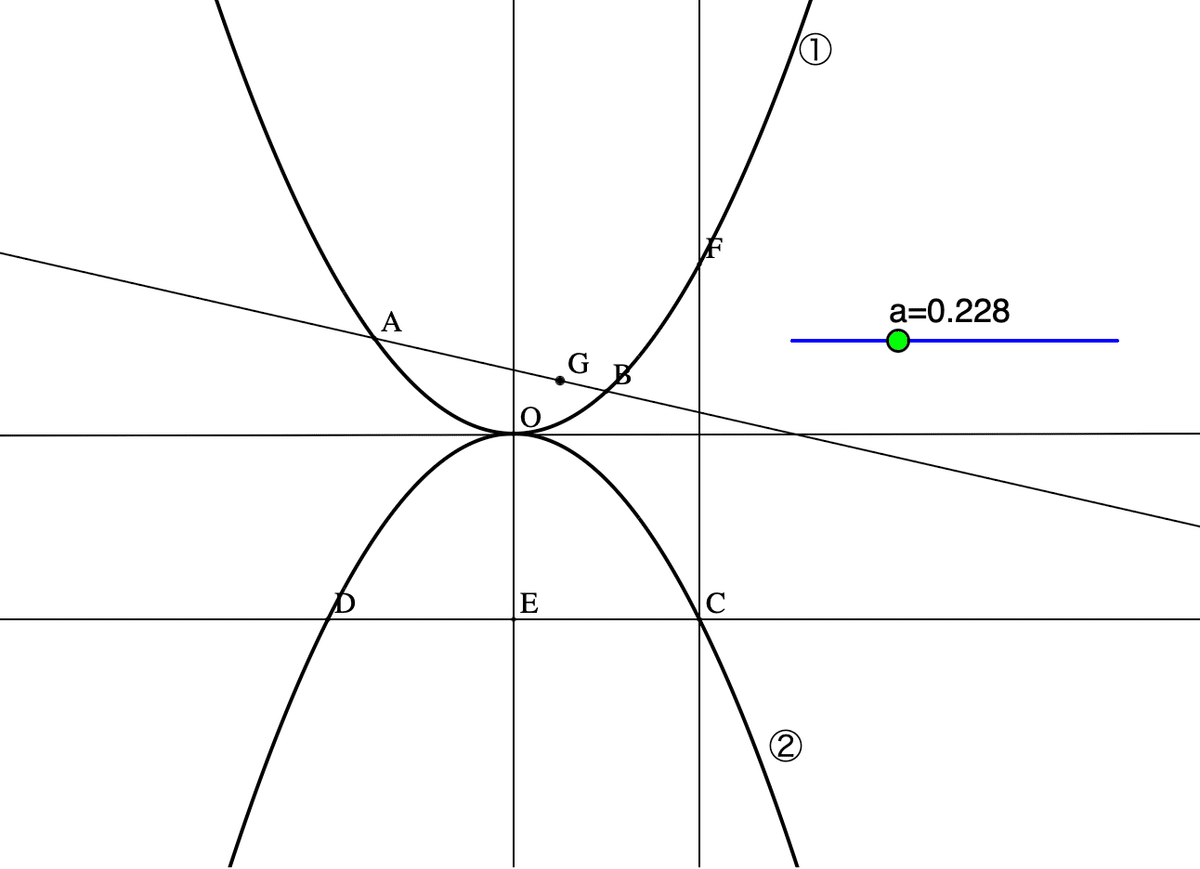
図の設定は次のようになっています。
①は,$${y=ax^2}$$ のグラフ
②は,$${y=bx^2}$$ のグラフ
2点A,Bは①上の点であり,その$${x}$$ 座標はそれぞれ -3, 2 である
点Cは②上の点で,その座標は$${(4,-4)}$$
点Dは,Cを通りx軸に平行な直線と②との交点
点Fは,Cを通りy軸に平行な直線と①との交点
点Gは直線AB上の点で,その$${x}$$ 座標は 1
問題は次の順に出ます。
まず $${b}$$ の値を求めます。これは簡単でしょう。
次に,$${a}$$の値を変化させたときの図の変化を考えます。ここが「タブレット端末を使って」というところです。このときの図の変化について述べたものとして,アからオまでの選択肢があり,その中で正しいものをすべて選びます。
ア $${a}$$の値を大きくすると,①のグラフの開き方は小さくなる。
イ $${a}$$の値を小さくすると,点 A の y 座標から点 B の y 座標をひいた値は大きくな る。
ウ $${a}$$の値を大きくすると、△OBEの面積は大きくなる。
エ $${a}$$の値を小さくすると、直線OBの傾きは小さくなる。
オ $${a}$$の値を大きくすると、線分CFの長さは短くなる。
さて,上のリンクを開いた図で,右方にあるスライダの緑の点をドラッグすると$${a}$$の値を変化させることができます。ア〜オのどれが正しいか,実際に動かしてみれば一目瞭然です。
最後に,3点D , G , F が一直線上にあるときの$${a}$$の値を求めます。これは,求める過程も書くことになっていますが,ちゃんと書くと結構な量になるでしょう。3点D , G , F が一直線上にあるときの$${a}$$の値については,計算する必要がありますが,$${a}$$ の値を動かして3点D , G , F が一直線上にあるようにすることで計算結果を検証することができるでしょう。
では,Cinderella での作図手順を説明しましょう。
まず,画面下のツールのうち,磁石のアイコンをクリックしておきましょう。グリッドが表示され,「格子点にスナップする」モードになります。なお,画面の背景色は,インスペクタで白にしています。
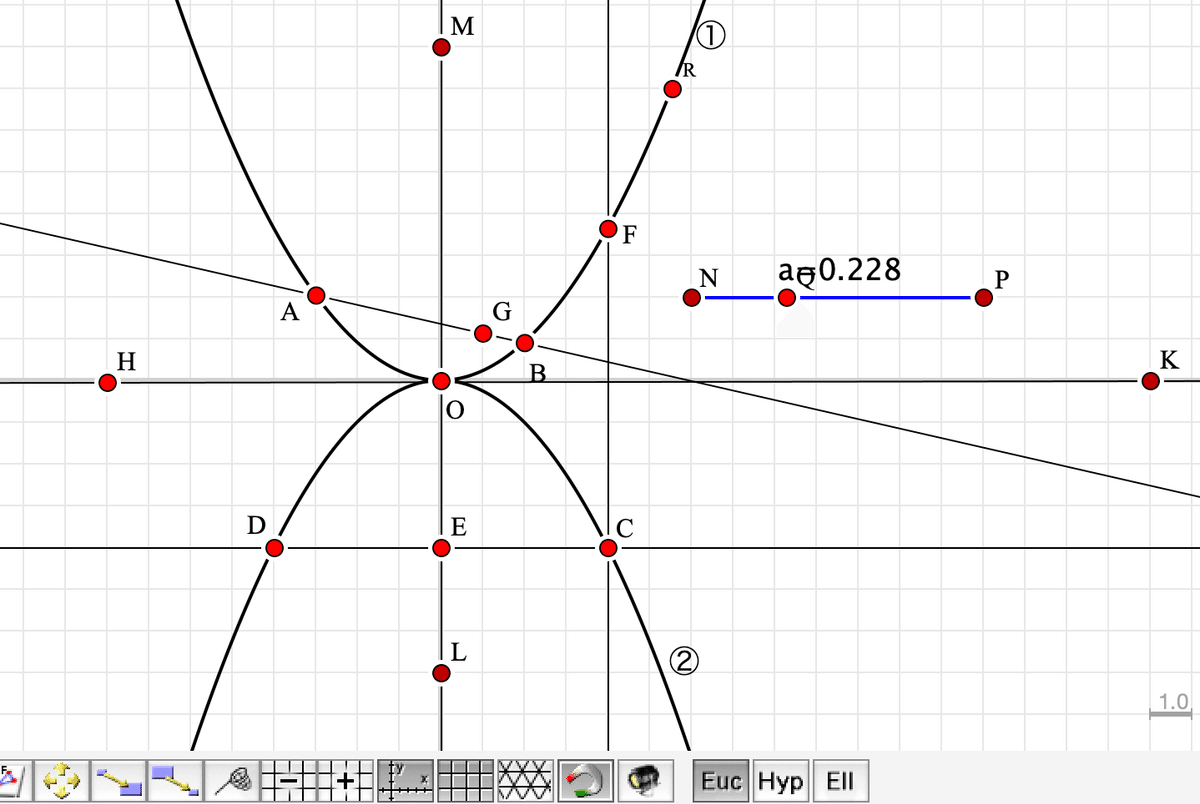
作図ツールで次のように点,直線を描きます。
(1) 点A, B, C, D, E, F, G を適当なところに置く。正しい位置はスクリプトで指定する。
(2) 座標軸として,直線ツールを用いて2本引く。(直線HKと直線LM)
このとき,背景に描かれている方眼の格子点の近くに持っていくと,吸い寄せられるように格子点につく(これがスナップ)
(3) 原点に点を取る(スナップ)。この点はインスペクタでOに名前を変える。
(4) スライダ用の線分を適当なところに引く(NR)
(5) 線分NR上に点を取る。
(6) ①を表示する位置の補助をする点Rを適当なところに置く。
(7) 点C, D , E は定点なので,それぞれの格子点にドラッグする。
なお,以上は一例なので,同じ図ができれば手順を変えても結構です。
スクリプトを書いて,放物線を描き,スライダからaの値を取得して,点の位置を指定します。
plot(-1/4*x^2, size->2, color->[0, 0, 0]);
a = |N,Q|/10;
drawtext(Q.xy + [-0.2, 0.4],"a=" + a, size->18);
plot(a*x^2, size->2, color->[0, 0, 0]);
A.xy = [-3, a*(-3)^2];
B.xy = [2, a2^2];
F.xy = [4, 16a];
f(x):= -ax + 6a;
G.xy = [1, f(1)];
R.xy = [sqrt(7/a), 7];
drawtext(R.xy + [0.6, 1], "①", size->18);
drawtext([5.5, -7], "②", size->18);f(x) は,直線ABを表す1次関数です。
うまく動いたら,インスペクタで点の大きさを変えたり,ラベルを非表示にするなどして体裁を整えます。また,背景の座標軸と方眼を非表示にします。
最後に,ファイルメニューからHTMLに書き出せばWeb上で使えるようになります。
