
インドラの真珠:2つの円
2つのメビウス変換とその逆変換で構成される反復関数系を考えます。これによってできる極限集合は数学的にも、美的にも特に面白いものです。
前節でおこなったような、3組の点の対応でできるメビウス変換から始めます。
2つの互いに交わらない円があり、それぞれの円周上の3つの点の組が対応します。
リンク先を開くと次の画面(左上・タイトル画像と同じ)が出ます。円の中心と円周をドラッグして位置や大きさを変えてみましょう。(右上,下)

明るい緑の点の像がこのメビウス変換と逆変換によって暗い緑の点につぎつぎと写ります。図では写った緑の点は数個に見えますが、実は十数個あります。重なっているので数個に見えるのです。
次の図では,もとの円そのものをメビウス変換と逆変換によって写します。
リンク先を開くと次の画面が出ます。

円が入れ子状態で小さくなりながら写っていきます。
これも,円の位置や大きさを変えてみましょう。円周上の3組の点の位置も変えてみましょう。

2つの円が接して、しかも接点がメビウス変換の定義をしている対応点である場合にどんな図形になるか、やってみてください。たとえば次のようになります。
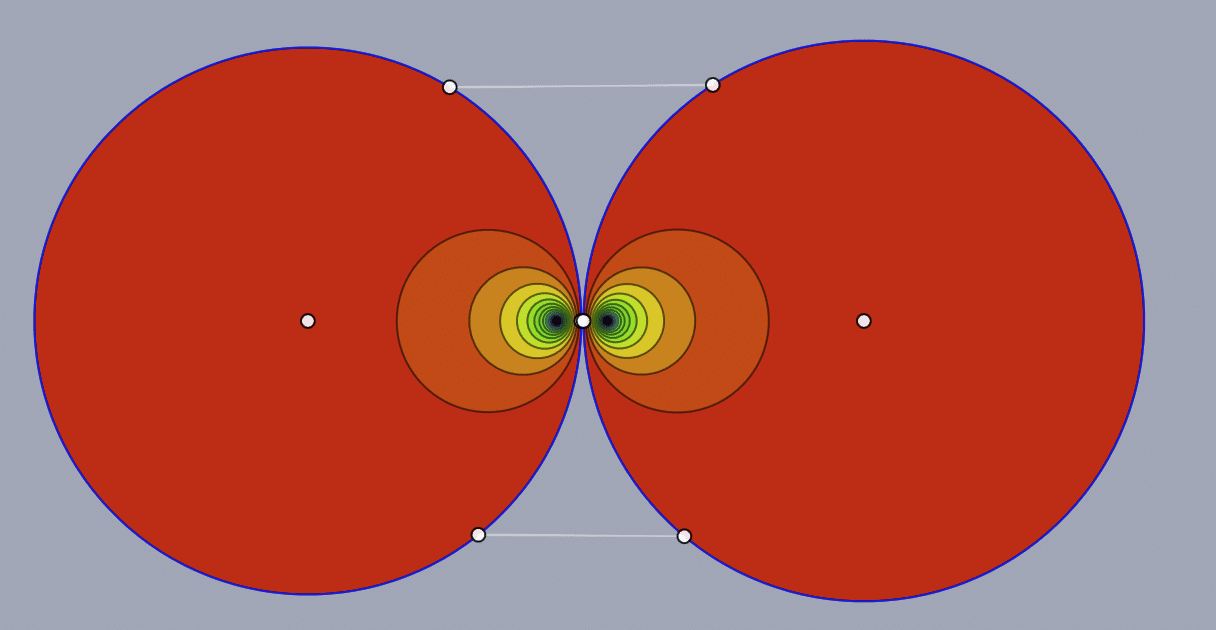
さて,現象はわかったでしょうが,何をしているのかを説明しましょう。
リンク先を開くと,背景が白になって,ボタンとスライダが追加された画面になります。

始めは円Aが選ばれています。反復回数のスライダを動かしてみましょう。

矢印でメビウス変換を定義した点の対応が表示されています。円Aの円周上の3点を円Bの3点に写すと,円は3点で決まりますので,円Aは円Bにそっくり写ることになります。円Aの中にある小円は,その変換の逆変換(B上の点をA上の点に写す)によって円Aを写した像です。
繰り返しを2にしてみましょう。

円Aの内部にあった円が,再び逆変換でその内部に写ります。
これを繰り返して,次々に円の内部に写っていくわけです。
「円A」のボタンをクリックして選択状態を解除し,今度は円Bを選んでみましょう。

両方の円を選べば,先ほどの図になるわけです。
→次節:ショットキー円
→インドラの真珠:目次 に戻る
