
自己平方フラクタル(2)ジュリア集合
自己平方フラクタル(1) マンデルブロ集合 で示した式
$${f(z)=z^2+ c}$$
で,$${c}$$ を固定し,初期値$${z_0}$$ の方を複素数平面上の各点にしたものをジュリア集合と呼んでいます。
Web上を「ジュリア集合」で検索すればたくさんのページがヒットします。掲載されたコードを実際に動かしてみると,表示されるまでに時間がかかるものがありました。
これだと,$${c}$$ の値を変えてやってみる,というのがそう簡単ではないでしょう。
CindyJSなら,インタラクティブに探索するものを作ることができます。マンデルブロ集合の場合と同じですが,使い方は少し異なります。
リンク先を開くとつぎの画面になります。
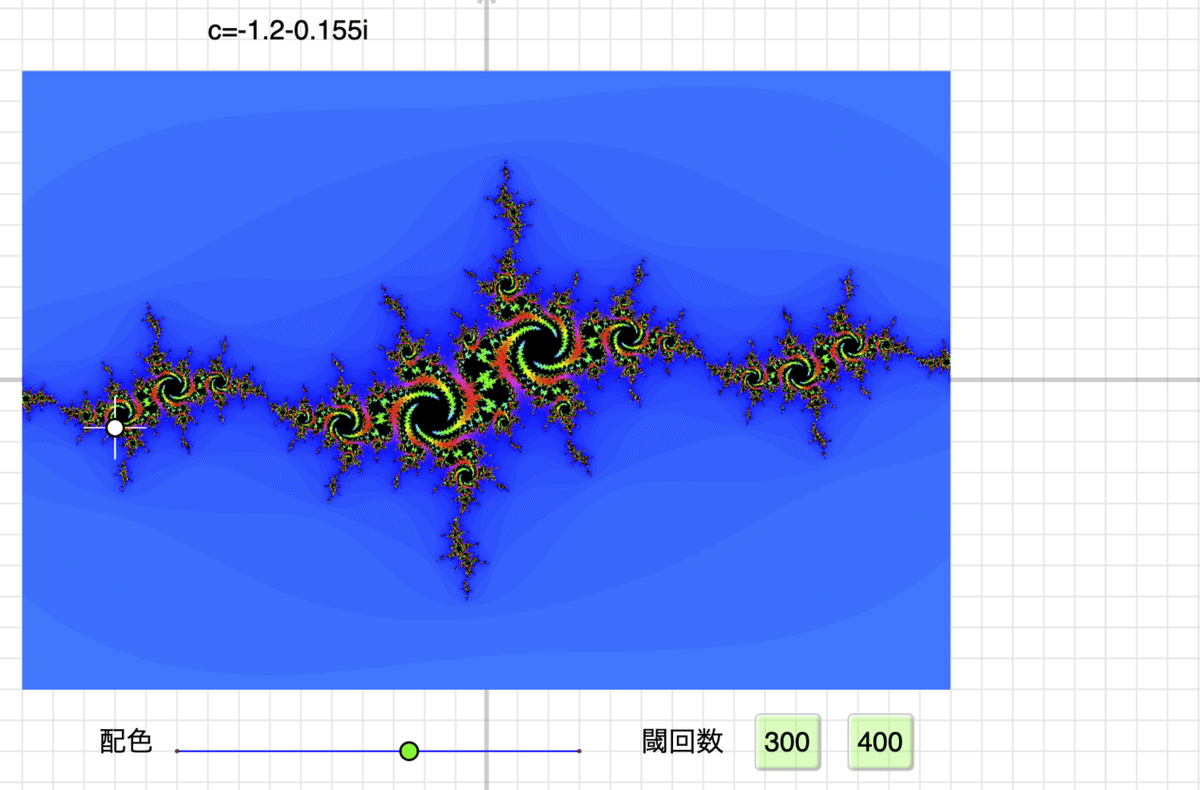
下方に配色のスライダと閾回数の2つのボタンがあります。「300」「400」のボタンが表示されていない場合は再読み込みしてください。この数値は,収束・発散の判定をするまでの繰り返し回数です。「閾回数」という言葉は造語です。
デフォルトは200です。これは,先に示した Python のプログラムの場合と同じですが,CindyJSなら一瞬で表示されるので,これから説明する使い方で探索をすることが可能になります。
300,400 にすると,図が変わります。場所によっては 300 と 400 でほとんど変わらない場合があります。その違いが興味深いのと,400だとさすがに反応が遅くなるのでデフォルトを200にしています。
「300」をクリックしてみましょう。

ボタンを押したときだけ図が変わります。画面上でマウスを動かすなどの操作をすると戻ります。
次に「400」をクリックしてみましょう。

渦巻きがかなり奥まで行きました。
もっと増やすことも可能ですが,あちこち探索して,400くらいまでやればよいだろうと判断しました。
配色のスライダで色が変わります。これは,色相環のスタート位置を変えているのです。
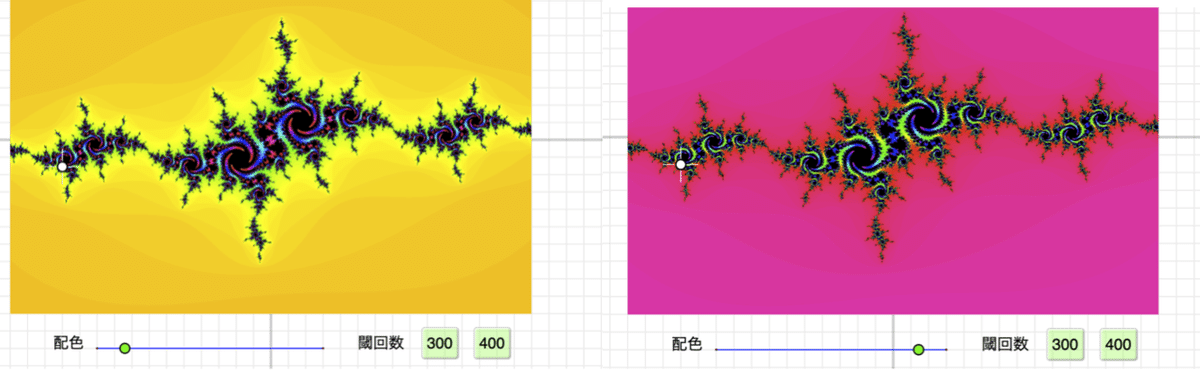
ま,ちょっとした遊びですね。
描画エリアは,横が -1.5〜1.5,縦が -1 〜1 です。c の初期値は上に表示されているように $${-1.2-1.55i}$$ です。これは「フラクタルCGコレクション 渕上季代絵 サイエンス社」の56ページにあるものです。左の方に白い点があるでしょう。それがこの点です。
では,cの値を変えてみましょう。左方にある白い点をドラッグしてみましょう。操作している様子をYoutube に載せました。
ほんのわずか点を動かしただけで図が変わるところがあります。ぜひ探索してみてください。
なお,スライダやボタンがなく,単に表示するだけのプログラムを載せておきます。CindyScriptです。CinderellaからHTMLに書き出せば CindyJS で動き,動作も速くなります。
c=-0.3-0.63*i;
n=200;
f(x):=(
z=complex(x);
k=0;
repeat(n,t,
if(abs(z)<2.0 & k<n,
z=z^2+c;
k=k+1;
);
);
if(k==n,col=0.7,col=k/n);
);
colorplot(hue(f(#)),[-1.5,-1],[1.5,1],pxlres->1);あらかじめ,画面下の「矩形領域を画面サイズに拡大」ツールで,方眼が0.1 になるまで拡大しておきます。その左の「平行移動」ツールも使って画面設定をしておくとよいでしょう。
次の図は n=400 の場合ですが(上のコードは n=200)表示されるまでかなり待たされるでしょう。n=200でも数秒かかります。HTMLに書き出せば,CindyJSのライブラリを読むまでに少し時間がかかりますが表示はかなり速くなります。

