
離散的な不連続点をもつ関数の積分
今回は「連続な関数は積分可能」という事実を踏まえ、少しの不連続点をもつ関数も積分可能かどうかを見ていきます。
1. どのような状況で生じるか
前回の記事https://note.com/euit353/n/n3cc3bd1dd961
で述べたように、部分積分の公式は $${f'(x)g(x)}$$ と $${f(x)g'(x)}$$ の積分を比較する公式と捉えることができました。そこでは暗に $${f(x)}$$ と $${g(x)}$$ が滑らかであるという仮定がなされており、そのおかげで $${f(x)}$$ と $${g(x)}$$ が定義されている区間では $${f'(x)g(x)}$$ と $${f(x)g'(x)}$$ も定義されていました。しかし実はこの現象は一般的には成り立ちません。
例1: 例えば $${f(x)=|x|}$$、$${g(x)=x}$$ としてみましょう。これらの関数は実数全体の上で定義されており、$${y=f(x)}$$ のグラフは下のようになります。しかし、原点では微分ができないため $${f'(x)}$$ は $${x=0}$$ では定義されていません。

したがってこの場合は $${f(x)}$$, $${g(x)}$$, $${f(x)g'(x)}$$ はいずれも実数全体で定義されていますが、$${f'(x)g(x)}$$ だけが原点では定義されていないことになります。
このような時に定義域を揃えるため以下のようにして拡張された関数を考えます。
この記事での約束:
関数 $${f}$$ に対してその定義域を $${D_f}$$ と表し、実数全体を定義域とする関数 $${\widetilde{f}}$$ を
$${\widetilde{f}(x)=\begin{cases}f(x) \ \ \ \ (x\in D_f)\\0 \ \ \ \ \ \ \ \ \ \ ({x\notin D_f})\end{cases}}$$
によって定める。
例2:例1のように$${f(x)=|x|}$$ とします。$${y=f'(x)}$$ のグラフは以下の通りです。

つまり原点でのみ定義されておらず、他の点では1という値をとります。よって $${f'(x)}$$ を拡張した $${\widetilde{f'}(x)}$$ は、原点でのみ0を補完して
$$
\widetilde{f'}(x)=
\begin{cases}
1 \ \ \ \ \ \ \ (x\neq 0)\\
0 \ \ \ \ \ \ \ ({x=0})
\end{cases}
$$
となります。
2. 連続関数は積分可能
積分はよく「関数のグラフと座標軸で囲まれた部分の面積」という説明がなされますね。見出しにある積分可能とは大雑把に言うとその面積がきちんと確定するということです。イメージを掴むため実際に積分できない例を見てみましょう。
例3: $${f(x)=\frac{1}{x^2}}$$ を拡張した関数 $${\widetilde{f}(x)}$$ を $${[-1, 1]}$$ で積分しようと試みます。もし積分値が存在するならば、これは$${1}$$未満の正数 $${\delta}$$ に対して $${f(x)}$$ を $${[-1, -\delta]}$$ および $${[\delta, 1]}$$ で積分した値、つまり下図の色がついた領域の面積よりも大きいはずです。
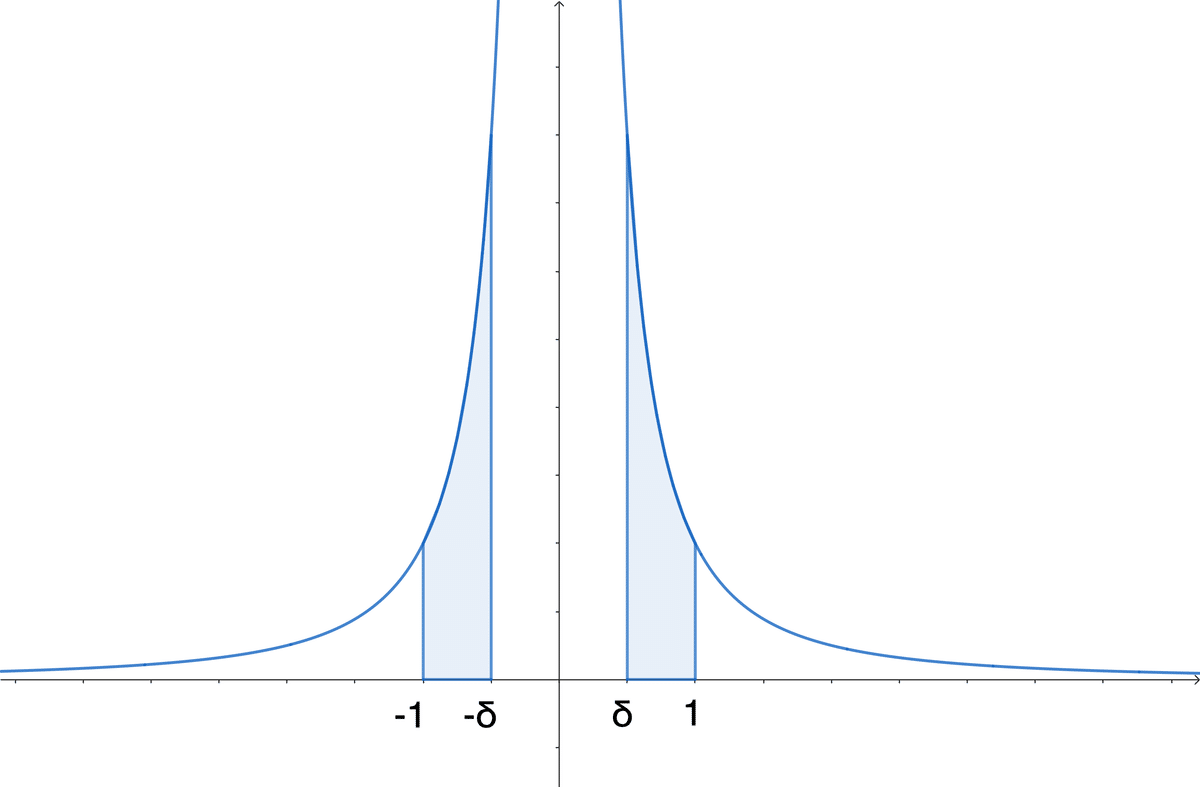
これを計算するには、対称性より片側の面積を求め2倍すればよいです。つまり
$$
\int^1_\delta \frac{1}{x^2}dx=\biggl[-\frac{1}{x}\biggr]^1_\delta=\frac{1}{\delta}-1
$$
の2倍で、$${2(\frac{1}{\delta}-1)}$$。これは $${\delta}$$ を $${0}$$ に近づけていくと発散してしまいます。つまり曲線$${y=\widetilde{f}(x)}$$と直線$${x=-1}$$, $${x=1}$$ および $${y=0}$$ で囲まれた部分の面積は定まりません。よって今考えていた積分はできません。
上の例では関数が不連続であることが問題を引き起こしています。実際、連続ならば次の定理よりこのような問題は生じません。
定理1:
連続な関数は、定義域に含まれる任意の有限閉区間で積分できる。
3. 区分的な連続性
では不連続点がある場合はいつ積分できるのでしょう。一つの十分条件として「区分的な連続性」があります。
関数 $${f(x)}$$ が区分的に連続であるとは、次の2条件が成り立つこと。
1. 離散的な点の集まりを除いた部分で $${f(x)}$$ は連続である。
2. $${f(x)}$$ が不連続になる点 $${a}$$ においても片側極限 $${\lim_{x\to a+0}f(x)}$$、$${\lim_{x\to a-0}f(x)}$$ は存在して有限値をとる。
条件1にある「離散的」とはくっついていないというイメージです。当然数学的に厳密な定義もありますが、それは有限区間内には有限個しかないと言い換えることができます。
例4: 例3で扱った $${f(x)=\frac{1}{x^2}}$$ 。これを拡張した $${\widetilde{f}(x)}$$ は区分的に連続ではありません。実際、 $${x}$$ を右側から $${0}$$ に近づけると $${{\widetilde{f}(x)}}$$ は発散します(左側から近づけても同じ)。よって条件2が満たされません。
例5: 例3の $${\widetilde{f}(x)}$$ に対して0の部分に幅を持たせた関数
$$
g(x)=
\begin{cases}
\frac{1}{x^2} \ \ \ \ (x<-\frac{1}{2}, x>\frac{1}{2})\\
0 \ \ \ \ \ \ \ (-\frac{1}{2}\leq x\leq \frac{1}{2})
\end{cases}
$$
を考えましょう。

これは区分的に連続です。実際、不連続になる点は $${x=\pm\frac{1}{2}}$$ のみであり、これらの点でも
$${\lim_{x\to \frac{1}{2}+0}g(x)=\lim_{x\to -\frac{1}{2}-0}g(x)=4}$$
$${\lim_{x\to \frac{1}{2}-0}g(x)=\lim_{x\to -\frac{1}{2}+0}g(x)=0}$$
というように確かに片側極限が有限値をとります。
では今回の主題である次の定理に移りましょう。
定理2:
区分的に連続な関数は、定義域に含まれる任意の有限閉区間で積分できる。
証明:区分的に連続な関数 $${f(x)}$$ とその定義域に含まれる有限閉区間 $${[a, b]}$$ を考えます。条件1より $${f(x)}$$ の不連続点は $${[a, b]}$$ に有限個しかないので、ある有限数列
$$
a=a_1<a_2<\cdots <a_n=b
$$
が存在して各開区間 $${(a_i, a_{i+1})}$$ ($${i=1,\ldots, n-1}$$)で連続となります。もし各々の $${\int_{a_i}^{a_{i+1}}f(x)dx}$$ が計算できればそれらの和が $${\int^b_af(x)dx}$$ となりますから主張が示されます。そこで区分的な連続性の条件2を用いて関数 $${f_i(x)}$$ を
$$
f_i(x)=
\begin{cases}
\displaystyle\lim_{t\to a_i+0} f(t)\ \ \ \ \ \ (x=a_i)\\
f(x) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (a_i< x < a_{i+1} ) \\
\displaystyle\lim_{t\to a_{i+1}-0}f(t)\ \ \ (x=a_{i+1})
\end{cases}
$$
で定義しましょう。するとこれは閉区間 $${[a_i, a_{i+1}]}$$ で連続ですから定理1より積分 $${\int^{a_{i+1}}_{a_i}f_i(x)dx}$$ の値が確定します。有限個の点での値を変えたところで積分には影響しないので、これは$${\int^{a_{i+1}}_{a_i}f(x)dx}$$ と等しいです。
(証明終)
例6: 例5で扱った関数 $${g(x)}$$ は定理2より任意の有限閉区間で積分可能です。例えば$${\int^1_{-1}g(x)dx}$$ は例2で計算した積分に$${\delta=\frac{1}{2}}$$ を代入した値、つまり $${2}$$となります。
この記事が気に入ったらサポートをしてみませんか?
