抵抗・インピーダンスのY結線とΔ結線変換

elemag

2023年12月11日 10:44

各端子から見た合成抵抗

電気回路で抵抗の合成を考えたように、電力系統の解析では、図1に示すY結線と図2に示すΔ結線を相互に変換することで、解析を容易にすることがある。今回は、相互変換する際の式を見ていく。

図1のa_b端子からみた回路は、図3のようになる。

よって、a_b端子から見た合成抵抗$${R_{{\rm{Ya\_b}}}}$$は、

$$
R_{{\rm{Ya\_b}}} = R_{Y1}+R_{Y2} \tag{1}
$$

となる。b_c端子、c_a端子から見た合成抵抗$${R_{{\rm{Yb\_c}}}}$$、$${R_{{\rm{Yc\_a}}}}$$も同様にして、

$$
\begin{align}
R_{{\rm{Yb\_c}}} &= R_{Y2}+R_{Y3} \tag{2} \\
R_{{\rm{Yc\_a}}} &= R_{Y3}+R_{Y1} \tag{3}
\end{align}
$$

と求まる。次に図2のa_b端子から見た回路は、図4のようになる。

図4は、接続点の位置をずらすと図5に示す並列回路になっていることが分かる。

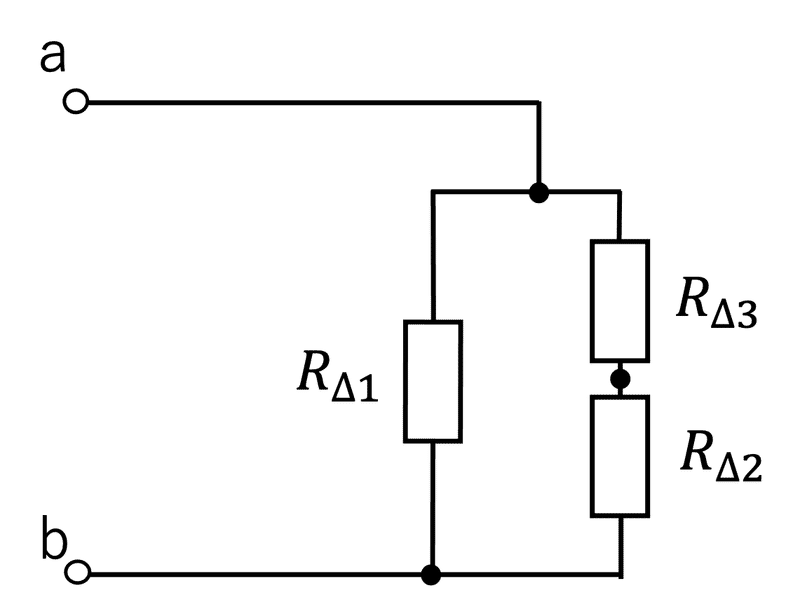
よって、a_b端子から見た合成抵抗$${R_{{\rm{\Delta a\_b}}}}$$は、

$$
R_{{\rm{\Delta a\_b}}} = \frac{1}{\frac{1}{R_{\Delta1}}+\frac{1}{R_{\Delta2}+R_{\Delta3}}}=\frac{R_{\Delta1}\left(R_{\Delta2}+R_{\Delta3}\right)}{R_{\Delta1}+R_{\Delta2}+R_{\Delta3}} \tag{4}
$$

と求まる。同様にして、b_c端子、c_a端子から見た合成抵抗$${R_{{\rm{\Delta b\_c}}}}$$、$${R_{{\rm{\Delta c\_a}}}}$$は、

$$
\begin{align}
R_{{\rm{\Delta b\_c}}} &= \frac{1}{\frac{1}{R_{\Delta2}}+\frac{1}{R_{\Delta3}+R_{\Delta1}}}=\frac{R_{\Delta2}\left(R_{\Delta3}+R_{\Delta1}\right)}{R_{\Delta1}+R_{\Delta2}+R_{\Delta3}} \tag{5} \\
R_{{\rm{\Delta c\_a}}} &= \frac{1}{\frac{1}{R_{\Delta3}}+\frac{1}{R_{\Delta1}+R_{\Delta2}}}=\frac{R_{\Delta3}\left(R_{\Delta1}+R_{\Delta2}\right)}{R_{\Delta1}+R_{\Delta2}+R_{\Delta3}} \tag{6}
\end{align}
$$

となる。Y結線とΔ結線を相互に変換するということは、各端子から見た合成抵抗は等しいということである。したがって、各端子から見た合成抵抗の式に次のような関係がある。

a_b端子

$$
\begin{align}
R_{{\rm{Ya\_b}}} &= R_{{\rm{\Delta a\_b}}} \notag \\
R_{Y1}+R_{Y2} &= \frac{R_{\Delta1}\left(R_{\Delta2}+R_{\Delta3}\right)}{R_{\Delta1}+R_{\Delta2}+R_{\Delta3}} \tag{7}
\end{align}
$$

b_c端子

$$
\begin{align}
R_{{\rm{Yb\_c}}} &= R_{{\rm{\Delta a\_b}}} \notag \\
R_{Y2}+R_{Y3} &= \frac{R_{\Delta2}\left(R_{\Delta3}+R_{\Delta1}\right)}{R_{\Delta1}+R_{\Delta2}+R_{\Delta3}}\tag{8}
\end{align}
$$

c_a端子

$$
\begin{align}
R_{{\rm{Yc\_a}}} &= R_{{\rm{\Delta a\_b}}} \notag \\
R_{Y3}+R_{Y1} &=\frac{R_{\Delta3}\left(R_{\Delta1}+R_{\Delta2}\right)}{R_{\Delta1}+R_{\Delta2}+R_{\Delta3}} \tag{9}
\end{align}
$$

Δ結線をY結線に変換する方法

まず初めに、図2のΔ結線を図1のY結線へと変換する方法についてみていく。各端子から見た合成抵抗の式(7)から式(9)を変形すれば良い。Δ結線をY結線へ変換する場合には、式(7)から式(9)を最終的に$${R_{Y1}=\cdots}$$、$${R_{Y2}=\cdots}$$、$${R_{Y3}=\cdots}$$の形に変形できれば良い。まずは、$${R_{Y1}}$$を求めていく。$${R_{Y1}}$$は、式(7)と式(9)にあり、$${R_{Y2}}$$と$${R_{Y3}}$$を消したいので、式(8)をうまく使うと消えそうである。そこで、式(7)から式(8)を引いてみると、

左辺

$$
\left(R_{Y1}+R_{Y2}\right) -\left(R_{Y2}+R_{Y3}\right) = R_{Y1}-R_{Y3} \notag
$$

右辺

$$
\left( \frac{R_{\Delta1}\left(R_{\Delta2}+R_{\Delta3}\right)}{R_{\Delta1}+R_{\Delta2}+R_{\Delta3}}\right) - \left(\frac{R_{\Delta2}\left(R_{\Delta3}+R_{\Delta1}\right)}{R_{\Delta1}+R_{\Delta2}+R_{\Delta3}}\right)
= \frac{R_{\Delta1}R_{\Delta3}-R_{\Delta2}R_{\Delta3}}{R_{\Delta1}+R_{\Delta2}+R_{\Delta3}}\notag
$$

となるから、

$$
R_{Y1}-R_{Y3} = \frac{R_{\Delta1}R_{\Delta3}-R_{\Delta2}R_{\Delta3}}{R_{\Delta1}+R_{\Delta2}+R_{\Delta3}} \tag{10}
$$

が得られる。次に式(9)と式(10)を足してみると、

左辺

$$
\left(R_{Y1}-R_{Y3} \right) +\left(R_{Y3}+R_{Y1}\right) = 2R_{Y1} \notag
$$

右辺

$$
\left( \frac{R_{\Delta1}R_{\Delta3}-R_{\Delta2}R_{\Delta3}}{R_{\Delta1}+R_{\Delta2}+R_{\Delta3}}\right) + \left(\frac{R_{\Delta3}\left(R_{\Delta1}+R_{\Delta2}\right)}{R_{\Delta1}+R_{\Delta2}+R_{\Delta3}}\right)
= \frac{2R_{\Delta1}R_{\Delta3}}{R_{\Delta1}+R_{\Delta2}+R_{\Delta3}}\notag
$$

が得られるから、$${R_{Y1}}$$は、

$$
R_{Y1} = \frac{R_{\Delta1}R_{\Delta3}}{R_{\Delta1}+R_{\Delta2}+R_{\Delta3}} \tag{11}
$$

となる。$${R_{Y2}}$$、$${R_{Y3}}$$も同じような手順で計算すると、

$$
\begin{align}
R_{Y2} &= \frac{R_{\Delta1}R_{\Delta2}}{R_{\Delta1}+R_{\Delta2}+R_{\Delta3}} \tag{12}\\
R_{Y3} &= \frac{R_{\Delta2}R_{\Delta3}}{R_{\Delta1}+R_{\Delta2}+R_{\Delta3}} \tag{13}
\end{align}
$$

が得られ、Δ結線をY結線へ変換することができる。また、今は抵抗で行ったが、インピーダンスにしても同様に成り立ち、

$$
\begin{align}
\dot{Z}_{Y1} &= \frac{\dot{Z}_{\Delta1}\dot{Z}_{\Delta3}}{\dot{Z}_{\Delta1}+\dot{Z}_{\Delta2}+\dot{Z}_{\Delta3}} \tag{14}\\
\dot{Z}_{Y2} &= \frac{\dot{Z}_{\Delta1}\dot{Z}_{\Delta2}}{\dot{Z}_{\Delta1}+\dot{Z}_{\Delta2}+\dot{Z}_{\Delta3}} \tag{15}\\
\dot{Z}_{Y3} &= \frac{\dot{Z}_{\Delta2}\dot{Z}_{\Delta3}}{\dot{Z}_{\Delta1}+\dot{Z}_{\Delta2}+\dot{Z}_{\Delta3}} \tag{16}
\end{align}
$$

となる。

Y結線をΔ結線に変換する方法

図1のY結線を図2のΔ結線へと変換する方法についてみていく。各端子から見た合成抵抗の式(7)から式(9)を変形していく。Y結線をΔ結線へ変換する場合には、式(7)から式(9)を最終的に$${R_{\Delta1}=\cdots}$$、$${R_{\Delta2}=\cdots}$$、$${R_{\Delta3}=\cdots}$$の形に変形できれば良い。まずは、$${R_{\Delta1}}$$を求めていくが、Δ結線への変換は少々トリッキーな部分もある。そのため、自身で手を動かし、式展開を追っていくことを推奨する。式(7)から式(9)を再掲する。

$$
\begin{align}
R_{Y1}+R_{Y2} &= \frac{R_{\Delta1}\left(R_{\Delta2}+R_{\Delta3}\right)}{R_{\Delta1}+R_{\Delta2}+R_{\Delta3}} \tag{7 再掲}\\
R_{Y2}+R_{Y3} &= \frac{R_{\Delta2}\left(R_{\Delta3}+R_{\Delta1}\right)}{R_{\Delta1}+R_{\Delta2}+R_{\Delta3}}\tag{8 再掲}\\
R_{Y3}+R_{Y1} &=\frac{R_{\Delta3}\left(R_{\Delta1}+R_{\Delta2}\right)}{R_{\Delta1}+R_{\Delta2}+R_{\Delta3}} \tag{9 再掲}
\end{align}
$$

式(7)をみると、分母である$${R_{\Delta1}+R_{\Delta2}+R_{\Delta3}}$$と分子の$${R_{\Delta2}+R_{\Delta3}}$$を消すことができれば、$${R_{\Delta1}}$$を求められそうである。そこで、まずは分子を消すことを考えてみる。式(8)と式(9)をかけてみると、

左辺

$$
\begin{align}
&\left(R_{Y2}+R_{Y3}\right) \left(R_{Y3}+R_{Y1} \right) \notag \\
&= R_{Y1} R_{Y2}+ R_{Y2}R_{Y3}+R_{Y3}R_{Y1} +R_{Y3}R_{Y3} \notag \\
\end{align}
$$

右辺

$$
\begin{align}
&\frac{R_{\Delta2}\left(R_{\Delta3}+R_{\Delta1}\right)}{R_{\Delta1}+R_{\Delta2}+R_{\Delta3}}\times \frac{R_{\Delta3}\left(R_{\Delta1}+R_{\Delta2}\right)}{R_{\Delta1}+R_{\Delta2}+R_{\Delta3}} \notag \\&=\frac{R_{\Delta2}R_{\Delta3}\left(R_{\Delta3}+R_{\Delta1}\right)\left(R_{\Delta1}+R_{\Delta2}\right)}{\left(R_{\Delta1}+R_{\Delta2}+R_{\Delta3}\right)^{2}}\notag \\
\end{align}
$$

となる。ここで右辺の$${\frac{R_{\Delta2}R_{\Delta3}}{R_{\Delta1}+R_{\Delta2}+R_{\Delta3}}}$$は、Δ結線をY結線に変換する際に求めた、式(13)の$${R_{Y3}}$$そのものである。よって、両辺を$${R_{Y3}}$$で割ると、

左辺

$$
\begin{align}
&\left(R_{Y1} R_{Y2}+ R_{Y2}R_{Y3}+R_{Y3}R_{Y1} +R_{Y3}R_{Y3}\right) \times \frac{1}{R_{Y3}}\notag \\
&=\frac{R_{Y1} R_{Y2}+ R_{Y2}R_{Y3}+R_{Y3}R_{Y1} }{R_{Y3}} +R_{Y3}\notag \\
\end{align}
$$

右辺

$$
\begin{align}
&\frac{R_{\Delta2}R_{\Delta3}\left(R_{\Delta3}+R_{\Delta1}\right)\left(R_{\Delta1}+R_{\Delta2}\right)}{\left(R_{\Delta1}+R_{\Delta2}+R_{\Delta3}\right)^{2}} \times \frac{1}{R_{Y3}}\notag \\
&=\frac{R_{\Delta2}R_{\Delta3}\left(R_{\Delta3}+R_{\Delta1}\right)\left(R_{\Delta1}+R_{\Delta2}\right)}{\left(R_{\Delta1}+R_{\Delta2}+R_{\Delta3}\right)^{2}} \times \frac{R_{\Delta1}+R_{\Delta2}+R_{\Delta3}}{R_{\Delta2}R_{\Delta3}} \notag \\
&=\frac{\left(R_{\Delta3}+R_{\Delta1}\right)\left(R_{\Delta1}+R_{\Delta2}\right)}{\left(R_{\Delta1}+R_{\Delta2}+R_{\Delta3}\right)}\notag \\
&=\frac{R_{\Delta1}R_{\Delta1}+R_{\Delta1}R_{\Delta2}+R_{\Delta1}R_{\Delta3}+R_{\Delta2}R_{\Delta3}}{\left(R_{\Delta1}+R_{\Delta2}+R_{\Delta3}\right)}\notag \\
&=\frac{R_{\Delta1}\left(R_{\Delta1}+R_{\Delta2}+R_{\Delta3}\right)+R_{\Delta2}R_{\Delta3}}{\left(R_{\Delta1}+R_{\Delta2}+R_{\Delta3}\right)}\notag \\
&=R_{\Delta1}+ \frac{R_{\Delta2}R_{\Delta3}}{\left(R_{\Delta1}+R_{\Delta2}+R_{\Delta3}\right)}\notag \\
\end{align}
$$

となる。またしても右辺第2項の$${\frac{R_{\Delta2}R_{\Delta3}}{R_{\Delta1}+R_{\Delta2}+R_{\Delta3}}}$$は、式(13)の$${R_{Y3}}$$そのものである。よって、両辺から$${R_{Y3}}$$を引くと、

左辺

$$
\begin{align}
&\frac{R_{Y1} R_{Y2}+ R_{Y2}R_{Y3}+R_{Y3}R_{Y1} }{R_{Y3}} +R_{Y3} -R_{Y3} \notag \\
&=\frac{R_{Y1} R_{Y2}+ R_{Y2}R_{Y3}+R_{Y3}R_{Y1} }{R_{Y3}} \notag \\
\end{align}
$$

右辺

$$
\begin{align}
&=R_{\Delta1}+ \frac{R_{\Delta2}R_{\Delta3}}{\left(R_{\Delta1}+R_{\Delta2}+R_{\Delta3}\right)} - R_{Y3}\notag \\
&=R_{\Delta1}+ \frac{R_{\Delta2}R_{\Delta3}}{\left(R_{\Delta1}+R_{\Delta2}+R_{\Delta3}\right)} -\frac{R_{\Delta2}R_{\Delta3}}{R_{\Delta1}+R_{\Delta2}+R_{\Delta3}} \notag \\
&= R_{\Delta1} \notag \\
\end{align}
$$

となる。よって、$${R_{\Delta1}}$$は、

$$
R_{\Delta1} = \frac{R_{Y1} R_{Y2}+ R_{Y2}R_{Y3}+R_{Y3}R_{Y1} }{R_{Y3}} \tag{17}
$$

となる。$${R_{\Delta2}}$$と$${R_{\Delta3}}$$も同様の手順で計算すると、

$$
\begin{align}
R_{\Delta2} &= \frac{R_{Y1} R_{Y2}+ R_{Y2}R_{Y3}+R_{Y3}R_{Y1} }{R_{Y1}} \tag{18} \\
R_{\Delta3} &= \frac{R_{Y1} R_{Y2}+ R_{Y2}R_{Y3}+R_{Y3}R_{Y1} }{R_{Y2}} \tag{19}
\end{align}
$$

と求められる。また、インピーダンスで考えた場合も同様に成り立ち、

$$
\begin{align}
\dot{Z}_{\Delta1} &= \frac{\dot{Z}_{Y1} \dot{Z}_{Y2}+ \dot{Z}_{Y2}\dot{Z}_{Y3}+\dot{Z}_{Y3}\dot{Z}_{Y1} }{\dot{Z}_{Y3}} \tag{20}\\
\dot{Z}_{\Delta2} &= \frac{\dot{Z}_{Y1} \dot{Z}_{Y2}+ \dot{Z}_{Y2}\dot{Z}_{Y3}+\dot{Z}_{Y3}\dot{Z}_{Y1} }{\dot{Z}_{Y1}} \tag{21} \\
\dot{Z}_{\Delta3} &= \frac{\dot{Z}_{Y1} \dot{Z}_{Y2}+ \dot{Z}_{Y2}\dot{Z}_{Y3}+\dot{Z}_{Y3}\dot{Z}_{Y1} }{\dot{Z}_{Y2}} \tag{22}
\end{align}
$$

となる。

静電容量のY結線とΔ結線変換
https://note.com/preview/n97a29c2660b9?prev_access_key=f99053e2309e649d1ee0fde04a0a8e91

Y結線
https://note.com/elemag/n/n69982181d762?sub_rt=share_pw

Δ結線
https://note.com/elemag/n/nbd92bde1cdcd?sub_rt=share_pw

抵抗の合成
https://note.com/elemag/n/n80cef07bc097?sub_rt=share_pw