座標系

座標系に必要な要素は、

• 軸

• 原点

• 大きさ1

の3つである。これがないと座標系になれない。

1次元座標

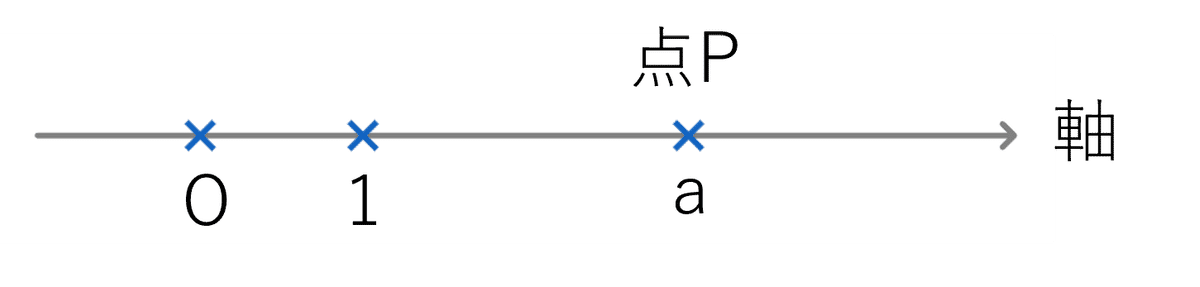
図1において、座標系に必要な3つの要素はすべてある。ここで、点Pを表すことを考える。
$${\frac{\mathrm{OP}の長さ}{\mathrm{O}と1の間の長さ}=\mathrm{a}}$$とすると、点Pの位置はaで表すことができる。
このように1つの数で表せる座標系を1次元座標系という。
また、Oから見て1の方向を正として扱い、反対方向は負として扱う。
点Pの位置を(a)のように書いて、これを座標という。
点Pの座標が(a)、点Qの座標が(b)のとき、PQ間の距離は、$${\sqrt{(a-b)^{2}}=|a-b|}$$で表される。

図1 1次元座標

直交座標系

直交座標はデカルト座標と言われることもある。特に2次元の場合は、平面座標ということもある。

2次元の直交座標

図2では、点Pの位置は2つの軸を用いることで表すことができる。また2つの軸は直交しており、直交した軸から構成される座標系を直交座標系という。点Pを表すには2つの数が必要である。そのため図2の座標系は2次元の直交座標系である。
点Pの位置は($${a_{1},a_{2}}$$)で表される。
図3に示すように点Pの座標を($${a_{1},a_{2}}$$)、点Qの座標を($${b_{1},b_{2}}$$)とすればPQ間の距離は$${\sqrt{(a_{1}-b_{1})^{2}+(a_{2}-b_{2})^{2}}}$$で表される。

図2 2次元直交座標

図3　2次元直交座標の距離

3次元の直交座標

図4では、3つの軸から座標系を構成している。点Pの位置は3つの数で表され、その座標は($${a_{1},a_{2},a_{3}}$$)となる。このように3つの数で表す座標系を3次元という。
3次元直交座標系における2点間の距離は、2次元直交座標系の距離に3次元目の項を追加するだけである。したがって、$${\sqrt{(a_{1}-b_{1})^{2}+(a_{2}-b_{2})^{2}+(a_{3}-b_{3})^{2}}}$$で表される。

図4　3次元直交座標

サイト

https://sites.google.com/view/elemagscience/%E3%83%9B%E3%83%BC%E3%83%A0