状態変数線図と状態変数変換　現代制御

状態変数線図

古典制御では、ブロック線図によって、システムの関係を図示していた。状態空間表現においても、ブロック線図のようなものを用いることで、システムの関係が理解しやすくなる。
変数$${x(t)}$$とこの変数を時間$${t}$$で微分した$${\dot{x}(t)}$$について、次のような関係が成り立つ。

$$
x(t) = \int_{0}^{t}\dot{x}(\tau){\rm{d}}\tau\tag{1}
$$

式(1)においては、$${\dot{x}(t)}$$を時間$${t}$$で積分したものが$${x(t)}$$であるとみることができる。
式(1)の関係を図示すると、図1のようになり、これを状態変数線図という。

図1 式(1)の状態変数線図

次に定数を$${a}$$として、微分方程式を考える。

$$
\dot{x}(t)=ax(t)\tag{2}
$$

式(2)では、$${\dot{x}(t)}$$が$${ax(t)}$$に等しいので、状態変数線図は、図2のようになる。

図2 式(2)の状態変数線図

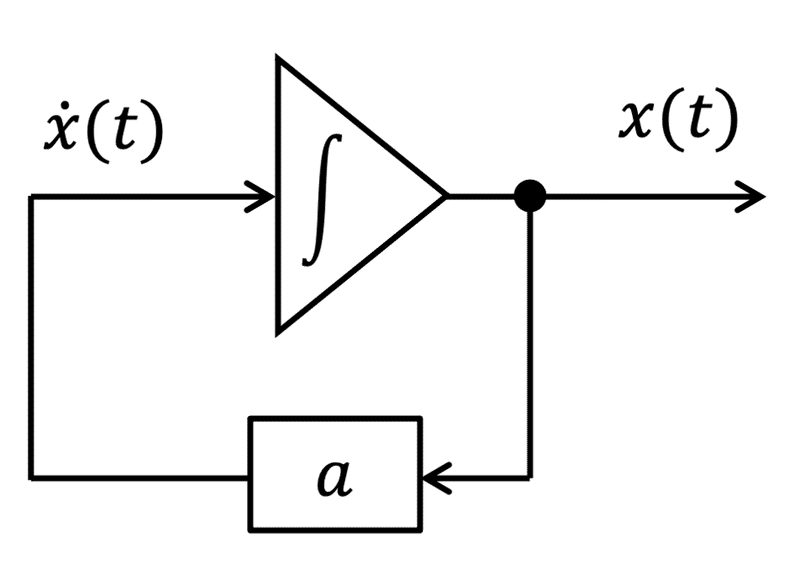
ベクトルで考える場合は、線を太くしたり、線の種類を変えて見やすくすることもある。式(2)をベクトルとした場合、

$$
\bm{\dot{x}}(t) = A\bm{x}(t)\tag{3}
$$

となる。状態変数線図は、図3となる。

図3 ベクトルの状態変数線図

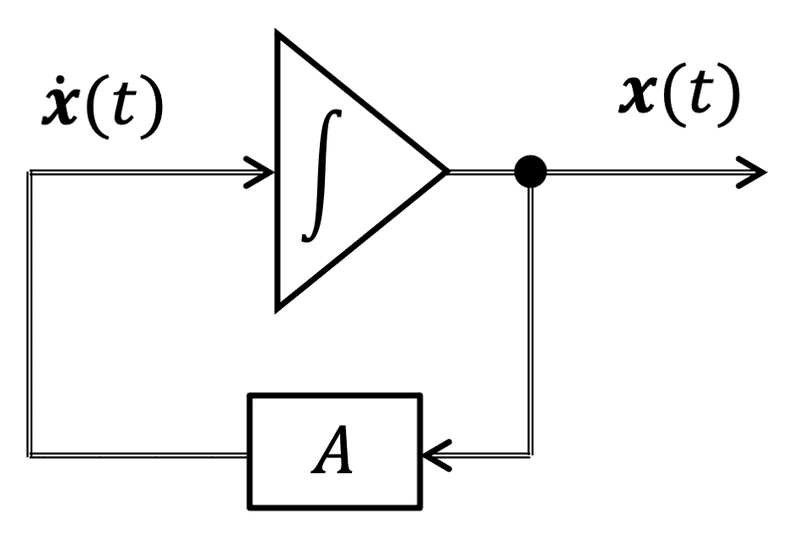
図3では、太線にするとあまりわからなかったので、二重線にしている。

状態変数変換

状態ベクトルを変換することで、システムの特性をより捉えやすくなることがある。
$${n}$$次元1入力1出力システムの状態空間表現が

$$
\begin{align}
\bm{\dot{x}}(t)&=A\bm{x}(t)+\bm{b}u(t)\tag{4}\\
y(t) &= \bm{c}\bm{x}(t)+du(t)\tag{5}\\
\end{align}
$$

であるとする。ここで、$${\bm{x}(t)}$$を$${n}$$次正則行列$${T}$$を用いて、

$$
\bm{x}(t)=T\bm{z}(t)\tag{6}
$$

に変換することを考える。$${T}$$は、正則かつ時間に無関係なので、

$$
\begin{align}
\bm{z}(t) &= T^{-1}\bm{x}(t)\tag{7}\\
\bm{\dot{x}}(t) &= T\bm{\dot{z}}(t)\tag{8}
\end{align}
$$

が成り立つ。よって、式(4)と式(5)は、それぞれ、

$$
\begin{align}
\bm{\dot{x}}(t)&=A\bm{x}(t)+\bm{b}u(t)\notag\\
T\bm{\dot{z}}(t)&=AT\bm{z}(t)+\bm{b}u(t)\notag\\
\bm{\dot{z}}(t)&=T^{-1}AT\bm{z}(t)+T^{-1}\bm{b}u(t)\tag{9}\\
y(t) &= \bm{c}\bm{x}(t)+du(t)\notag\\
&= \bm{c}T\bm{z}(t)+du(t)\tag{10}\\
\end{align}
$$

となる。これを状態変数変換といい。$${T}$$を状態変換行列という。
次に、状態変数変換した場合の伝達関数を見ていく。式(4)および式(5)から求まる伝達関数は、関連記事の状態空間表現と伝達関数表現の関係で求めたように、入力$${U(s)}$$から出力$${Y(s)}$$までの伝達関数$${G(s)}$$は、

$$
G(s) =\frac{Y(s)}{U(s)} = \bm{c}\left(sI-A\right)^{-1}\bm{b}+d\tag{11}
$$

であった。式(9)を初期ベクトル$${\bm{z}(0)=0}$$として、両辺ラプラス変換すると、

$$
\begin{align}
s\bm{Z}(s)&=T^{-1}AT\bm{Z}(s)+T^{-1}\bm{b}U(s)\notag\\
\left(sI-T^{-1}AT\right)\bm{Z}(s)&=T^{-1}\bm{b}U(s)\notag\\
\bm{Z}(s)&=\left(sI-T^{-1}AT\right)^{-1}T^{-1}\bm{b}U(s)\tag{12}\\
\end{align}
$$

となる。なお$${\bm{Z}=\mathcal{L}[\bm{z}(t)]}$$としている。
ここで、$${T^{-1}T=TT^{-1}=I}$$であること、$${s}$$はスカラーであること、単位行列は$${AI=IA=A}$$が成り立つこと、そして行列の分配法則を用いて、式(12)は、

$$
\begin{align}
\bm{Z}(s)&=\left(sI-T^{-1}AT\right)^{-1}T^{-1}\bm{b}U(s)\notag\\
&= \left(sT^{-1}T-T^{-1}AT\right)^{-1}T^{-1}\bm{b}U(s)\notag\\
&= \left[\left(sT^{-1}-T^{-1}A\right)T\right]^{-1}T^{-1}\bm{b}U(s)\notag\\
&= \left[\left(T^{-1}TsT^{-1}-T^{-1}A\right)T\right]^{-1}T^{-1}\bm{b}U(s)\notag\\
&= \left[T^{-1}\left(TsT^{-1}-A\right)T\right]^{-1}T^{-1}\bm{b}U(s)\notag\\
&= \left[T^{-1}\left(sTT^{-1}-A\right)T\right]^{-1}T^{-1}\bm{b}U(s)\notag\\
&= \left[T^{-1}\left(sI-A\right)T\right]^{-1}T^{-1}\bm{b}U(s)\tag{13}\\
\end{align}
$$

となる。ここで、$${\left(ABC\right)^{-1}=C^{-1}B^{-1}A^{-1}}$$であることを利用して、式(13)は、

$$
\begin{align}
\bm{Z}(s) &= \left[T^{-1}\left(sI-A\right)T\right]^{-1}T^{-1}\bm{b}U(s)\notag\\
&= T^{-1}\left(sI-A\right)^{-1}TT^{-1}\bm{b}U(s)\notag\\
&= T^{-1}\left(sI-A\right)^{-1}\bm{b}U(s)\tag{14}\\
\end{align}
$$

となる。
式(10)の両辺をラプラス変換すると、

$$
Y(s)= \bm{c}T\bm{Z}(s)+dU(s)\tag{15}
$$

となる。よって、伝達関数$${G(s)}$$は、

$$
\begin{align}
Y(s)&= \bm{c}T\bm{Z}(s)+dU(s)\notag\\
&= \bm{c}TT^{-1}\left(sI-A\right)^{-1}\bm{b}U(s)+dU(s)\notag\\
&= \left( \bm{c}TT^{-1}\left(sI-A\right)^{-1}\bm{b}+d\right)U(s)\notag\\
&=  \left( \bm{c}\left(sI-A\right)^{-1}\bm{b}+d\right)U(s)\notag\\
G(s)&=\frac{Y(s)}{U(s)} = \bm{c}\left(sI-A\right)^{-1}\bm{b}+d\tag{16}
\end{align}
$$

となる。これは、式(11)で示した伝達関数と同じである。したがって、状態変数を変換しても、入力から出力までの伝達関数は変化しないことがわかる。そのため、状態空間表現から伝達関数表現への変換は、1通りに求まることがわかる。

関連記事

状態空間表現と伝達関数表現の関係
https://note.com/elemag/n/n3421407b24a2?sub_rt=share_pw

サイト

https://sites.google.com/view/elemagscience/%E3%83%9B%E3%83%BC%E3%83%A0