【天鳳】期待値はあなたを裏切るか

まずは、この記事を読んでもらいたい。

chanpukuさんは大学生らしいが、目を疑うほど秀逸な記事だ。こりゃ麻雀界の未来は明るい。天鳳位のタケオしゃんさんも絶賛。

面白かったです^^ https://t.co/2TgkQeirij

— タケオしゃん＠麻雀動画クリエイター of 天鳳位 (@nyankosan) July 6, 2020

私も、目から鱗をボロボロ落としながら読ませてもらったのだが、同時に何かおかしいという違和感を覚えた。三日三晩考え続けて、ようやくその正体が見えてきたので、記事にまとめる。断っておくが、chanpukuさんの記事を批判する意図はなく、何が正しいのか皆さんにも考えて欲しいと考えて執筆してる(のでシェアして下さいお願いしますお願いしますお願いします)。

ちなみに、この記事は数学的に麻雀を議論する、ガチ理系向け記事となっておりますので、最強雀士を志す方はzeRoさんの麻雀戦術Noteへ、ZERO秒でGO！

https://note.com/zeromaxbet/m/m064cd6abcad7

最初に、結論から述べておこう。

① 昇段確率は、戦略を評価するのには優れた指標だが、打牌選択の基準に用いる事はできない。

② 昇段確率を最大にする戦略が、段位pt期待値を最大にする戦略に勝るという保証はない。

批判しないと言っておいて、見事にchanpukuさんの記事の逆張りです。ｽﾐﾏｾﾝ

なぜ昇段確率？

chanpukuさんの記事の内容を一部要約する。

天鳳において成績の優劣は昇段確率で評価されるべきで、昇段確率は「K」という指標が増加すれば一緒に増加する。

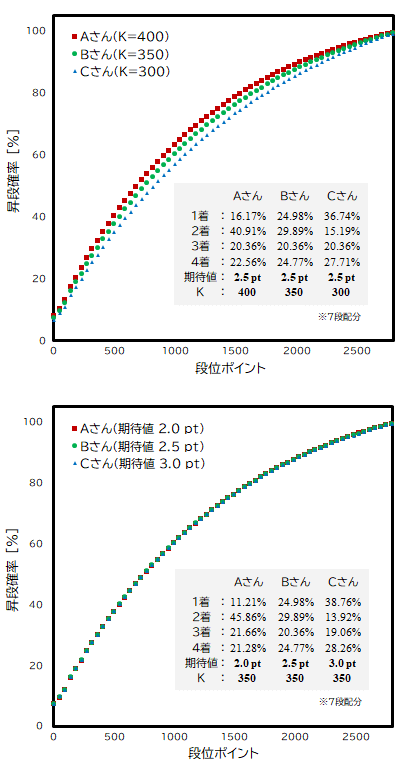
上の図では、段位ptの期待値が同じ三人でも昇段確率にズレがある事が分かる。逆に下の図では、段位ptの期待値が違っても「K」が一緒なので昇段確率が一緒だ。つまり、段位pt期待値よりも「K」の最大化（＝昇段確率の最大化）を目指すのが「最適戦略」だという結論だ。期待値厨からすれば「マジかよ……ｼﾆﾀｲ」だ。

極端な例で言えば、100%二着が取れるAさんと、90%で一着になれるが10%で四着となるBさんがいたとする。段位pt期待値はBさんの方が高いが、地獄を引けば降段する可能性はゼロではない。一方、Aさんは100%昇段できるので、Aさんの方が偉いということになる。

上記のNoteでは、この話がめちゃめちゃ分かりやすくまとめられてるんで、読んでみてください！(昇段確率関数が変曲面のない単調増加関数という点も非常に重要な発見だが、長くなるので今回は触れない。chanpukuさんすみません。)

昇段確率による戦略の評価

さて、本題に移ろう。もう一度繰り返すが、「昇段確率が最大（＝「K」が最大）となる戦略が、天鳳における最適戦略」であり、この点は私も100%同意見だ。問題は「昇段確率が最大となる戦略」ってなんなの？という点だ。

天鳳で「戦略」といっても二種類考えられる。一つは「どう打つか」という打牌戦略で、もう一つは「どの打ち方が良いか」という評価戦略だ。分かりにくいので、みんな大好きMリーグで例えよう。

打牌戦略とは、単純にどんな麻雀を打つかという戦略だ。園田賢なら「期待値の最大化」だし、萩原聖人なら「面白く」だ(ディスってないです)。つまり、「何を基準に打牌するか」という意味の戦略だ。

評価戦略とは、それぞれの各選手の戦略をどう評価するかという戦略だ。パイレーツは「デジタル」を評価する戦略で、コナミなどは「連盟員」を評価する戦略だ(連盟好きです)。つまり、「どいつの打牌戦略が優れてるか」評価するための戦略だ。

---------

突然ですが、ここからは少し数学的な話を混ぜます。分かりやすく説明しますが、読みたくない方は代わりに世界一の美女に3分半あげて下さい。

---------

麻雀とは、打牌戦略を変えることで結果が変わるゲームだ。「トップ率最大」戦略と「ラス回避」戦略では、着順分布が大きく変わる。これを変態的に数式で表現すれば、麻雀とは「打牌選択の戦略（S）」が入力値、「着順分布などの結果（p）」が出力値の関数である。(このNoteでは「結果 = 着順の確率分布」と解釈して下さい。)

そして、得られた結果を基にどの戦略が良かったかを考える事になる。トップ率30%、ラス率25%となる戦略と、トップ率25%、ラス率20%となる戦略のどっちが偉いかは、このときの評価戦略によるわけだ。そして、chanpukuさんの成果により、評価戦略に昇段確率・Kを使うのが正しいと示された。ｱﾘｶﾞﾄｳｺﾞｻﾞｲﾏｽ

上の画像では、みかん太さんとOMANTAさんの打牌戦略を比較するために、それぞれの結果から昇段確率係数(K)を求めている。くどいようだが、この時に段位pt期待値で比べちゃいけませんよということが示されたわけだ。もし、 みかん太さんのKの方が高いと分かれば、段位pt期待値に関わらず彼女の実力が上と評価することができる。(下ネタの実力はOMANTAさんの圧勝です。)

注意して欲しいのがここで使っているのは、評価戦略としての「昇段確率最大化」という点だ。私が疑問に思っているのはここではない。天鳳の最適戦略といえば、絶対的に地球最強の打牌戦略のことを指すのが一般的だと思うが、打牌戦略に昇段確率を取り入れると話が違うぜ？という指摘をさせてもらいたい。

昇段確率による打牌の選択

ここからが、本当の本当の本題だ。頑張ってついてきて下さい。「昇段確率が最大になる打牌戦略」はどうすれば見つけられるだろうか？

期待値を最大化したければ、期待値が最大になる選択肢を選び続ければいい。では、昇段確率を最大化したければ、昇段確率が最大になる選択肢を選び続ければいい。

「当たり前だろ！！ﾊﾞｰｶﾊﾞｰｶ‼︎‼︎‼︎」

と言わずによく聞いて欲しい。これって実はすごく難しい。どれくらい難しいかといえば、多井隆晴とわせりんさんが地球滅亡まで議論し続けても絶対無理なレベルだ。しかし、chanpukuさんは↓のような分かりやすい図でこれができるという説明をしている。

つまり、この図が間違っているか、私が間違っているかの二択だ。皆さんにも考えていただきたい。図の意味を簡単に説明すれば、昇段確率最大の選択肢を選ぶためには、まず各着順のときの昇段確率を求めて、その昇段確率の期待値が最大となるものを選びなさい、となる。

さて、私の考えでは、選択肢Aと選択肢Bで同じ昇段確率関数を使っている点が誤りだ。先程数式で示したとおり、麻雀は打牌戦略によって結果(着順分布)が変わるゲームだ。そして、選択肢Aと選択肢Bからどちらかを選ぶという行為は、まさに「打牌戦略A」と「打牌戦略B」を選ぶ行為に他ならない。つまり、どちらの選択肢を取るかで着順分布が変わるはずであり、着順分布が変われば昇段確率関数が変わると考えるのが自然だ。

「いや、こんな一回の選択で着順分布なんてかわんねーよ、ｸｿ ｦﾀｸ ﾔﾛｳｶﾞ」

と思われるかもしれないが、着順分布が変わらないと仮定すれば、結果的に昇段確率も変わらない事になってしまう。なぜなら、昇段確率は着順分布によって決定するからだ。逆にいえば、昇段確率は、着順分布を変えた時に初めて変わるはずだ。

つまり、選択肢によってそれぞれ別々の昇段確率関数を用意しなければいけない事になる。

しかし、昇段確率関数は、その戦略がどのような結果に結びつくかを完全に予測できなければ求める事ができない。そして、戦略と結果の関係は「麻雀」という関数を完全に理解するまでは明らかにならないのだ。つまり、実質不可能だ。

難しすぎるので具体例で説明しよう。今、七段に初めてなった養分が、「俺は最強だ」と意気揚々と鳳凰卓に挑んだとしよう。鳳凰卓が初めての養分は、自分の着順分布がまだ分からないので、当然「昇段確率の最大化」という戦略はとれない。つまり、しばらくは養分戦略で打つしかない。しばらくたってから、昇段確率を最大化する戦略に切り替えようと思っても、昇段確率の計算に使うことができるのは、養分戦略で戦ったときの着順分布だけだ。つまり、見た目では昇段確率が最大化されていたとしても、間違った昇段確率関数を基に計算をしているので、昇段確率が最大化されている保証がどこにもない。こうして養分はチャオってしまう。(と言ってる私の最高段位は七段です。)

実は「昇段確率を最大化する打牌戦略」と「段位pt期待値を最大化する打牌戦略」は根本的に異なる。段位pt期待値の計算は、その半荘の着順分布が予測できれば可能だ。一方、昇段確率の計算では、まだ始まっていない半荘における自分の着順分布まで予測しなければいけない。この絶対的な性質の違いが、「昇段確率を最大化する打牌戦略」を見つけることを困難にしているのだ。

期待値は裏切り者か

以上の議論が正しいとすれば、昇段確率を最大化する選択肢が一体なんなのかは、誰にも分からない。言えることは、昇段確率が最大となる戦略が仮に見つかったとすれば、それが天鳳における最適戦略ということだけだ。

では、今一度考えて欲しいのだが、期待値を最大化する戦略は最適戦略ではないのだろうか？昇段確率の最大化が最適戦略とすれば、期待値の最大化は最適戦略ではない、と考えるのが自然だ。

いや、ちょっと待って欲しい。実はまだ、期待値厨を救う希望が残っている。

それは、期待値を最大化する戦略と昇段確率を最大化する戦略が一致する場合だ。つまり、実は二つが全く同じ戦略であった場合だ。期待値最大化戦略は土俵際まで追い込まれているが、まだ負けてはない。この例外が否定できた時に初めて、期待値は天鳳民を裏切る事になるのだ。

結論

① 昇段確率は、天鳳における評価戦略として適している。

例えば、あなたが沢崎誠のようなベテランで、どんな打牌戦略を採用すれば着順分布がどうなるのか、予想がつくとする。この場合、段位pt期待値ではなく、昇段確率が最大となるような戦略を採用して打てば良い。そして、本文では触れていない重要な事実として、この戦略の選定は、昇段・降段した直後のみ行うべきだ。つまり、昇段や降段が近いからといって打ち方を変える行為は常に損である。(詳細は割愛)

② 昇段確率を考慮して打牌の選択をすることは、実質不可能である。

例えばAIなどが、最適だと思われる打牌を選ぶ際に、昇段確率を基準にすることはできない。なぜなら、AIが観測できるのはあくまでもその時点での着順分布から算出される見かけの昇段確率であり、これを基に戦略を決めても昇段確率が最大化される保証はない。これは①で述べた「戦略を途中で変えるな」という話とも整合性がある。

③ 段位pt期待値を最大化する打牌戦略は、天鳳における最適戦略である可能性がある。

昇段確率を最大化する打牌戦略がどんなものであるのか実質分からない以上、段位pt期待値を最大化する打牌戦略を採用した結果、昇段確率も同時に最大化される可能性は否定できない。ただし、①でも述べた通り、複数の戦略の中で段位ptが最大のものと、昇段確率が最大のものが別であれば、それらの中での「最適戦略」は、昇段確率が最大の戦略である。こういった意味で、chanpukuさんの「天鳳の最適戦略≠段位pt期待値の最大化」という表現は正しいと言える。現実的には、打牌を選択する時点で他に採用出来る良い基準がないため、今以上に強くなることを目指している人は「段位pt期待値の最大化」という打牌戦略を採用するべきだ、というのが私のスタンスだ。

もう一度はっきりと述べておくが、chanpukuさんのNoteは秀逸だ。ここまでわかりやすく自分の考えとその根拠を表現し、他人を説得出来る方は中々いないだろう。そして、得られた結果は極めて有益で、多くの人の「最適戦略」に対する考え方を変える大きな転機となったのは間違いないだろう。もちろん、私もその一人だ。改めて、敬意を表したい。

これまでにも、とつげき東北さん、みーにんさん、nisiさん、電脳麻将(小林さん)、爆打、NAGA、Suphxなどをはじめ、多くの方々が数学的アプローチで麻雀に取り組み、素晴らしい成果を上げてきた。一方で、将棋やポーカーと比較して、麻雀における理論的アプローチが占める役割はまだまだ小さいだろう。麻雀のゲーム性による部分もあると思うが、多くの人がまだ理論的アプローチの有効性を認識していないためだと思う。もちろん娯楽としての麻雀に大きな価値があるのも事実だが、このような議論を活発化させて「麻雀」というゲームをさらに進化させていくことも、麻雀界を発展させる一つの手段じゃないだろうか。(つまり、麻雀界の発展のためにこのNoteをシェアしてね♡ってことです。)

本記事の内容について、私自身も100%の自信があるわけではない。皆さんの意見、感想、反論お待ちしています。貴重な時間をありがとうございました。

※nisiさんをNishiさんと誤記していました。訂正してお詫びします。申し訳ありませんでした。(7/12 1:00)