【マンガ】統計学が最強の学問である　第4話補足〜統計モデルの作り方〜

統計モデルとは何か　

　第4話の冒頭で貴子は「統計モデル」という言葉を使いました。「統計モデル」とは、現実の現象を「よく模している」数式を統計データから作ったものです。プラモデルは現実にはプラスチックでできていない、自動車や飛行機や架空の世界のロボットなどを、プラスチックを使って「よく模したもの」ものですが、統計モデルもこれと同じです。

　必ずしも数学的に決定されているわけではない、自然や社会の現象に対して「統計を使ってよく模している数式」を作ろうしたものが統計モデルだと言うことができます。

　より具体的に言うと、作中で貴子が用いた統計モデルは「線形モデル」と言われるごく一般的に使われるものです。線形とは「直線的」というような意味で、何かの説明変数（たとえば「購買に占める土曜日の割合」など）が1増えるごとの、アウトカム（ライジンビールの年間購買金額）の変化量は「常に一定だったとしよう」と仮定するモデルです。

　ごく単純に、説明変数がこの「購買に占める土曜日の割合」たった1個の場合のイメージを図解すると、線形モデルはこんな感じになります。

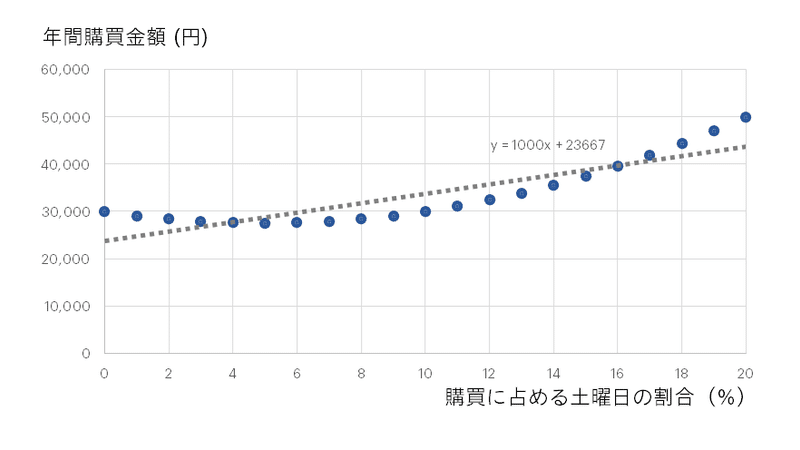
　慣例的に統計学では横のx軸に説明変数（今回は購買に占める土曜日の割合）、縦のy軸にアウトカム（年間購買金額）をグラフに示します。仮に、土曜日の割合が0%の人から、20%の人まで1人ずつ、丸で示すような21人のお客さんがいたとしましょう。土曜日の割合が0%のお客さんは年間3万円ライジンビールを買ってくれていますが、5%のお客さんはそれより少なく、27,500円しか買ってくれません。しかし、全体として土曜日にお買い物する割合が高い人ほどライジンビールをよく買ってくれているようで、土曜日の割合が20%のお客さんは年間5万円も買ってくれています。この状況で「土曜日の割合が1%増えるごとの、ライジンビールの購買金額の変化量は一定だとしよう」と仮定すると、おそらく点線で示すような直線で予測するのがよさそうだ、ということになりました。

単回帰分析：線形回帰モデルの基礎知識

　このように「単一の説明変数を使ってあてはまりのよい線形な直線を考える」ことを単回帰分析と呼びます。

　なお、統計モデルが「よさそうだ」というのは、基本的に統計モデルによるアウトカムの予測値と、実際のアウトカムの値のズレが全体としてできるだけ小さいものである状態のことを言います。プラモデルでも、「模そうとしているもの」より余計に出っ張っていたり、逆に余計に引っ込んでいるところが多いことを「精度が悪い」と表現しますが、統計モデルもそれと同様に、「仮定を満たす中でいちばん精度のよい数式は何か？」と考えてデータからそれを決めるわけです。

　数式と言っても今回の場合はただの直線なので、中学校で習う「y=ax+b」といったただの一次関数で表されます。今回の場合、

購買金額　=　1000　×　土曜日の割合　＋　23667

となっており、「ｘ（土曜日の割合）が1%増えるごとに1000円ずつ購買金額が高い傾向にある（中学校で習う『傾き』）」「ｘ（土曜日の割合）が0%のときには23667円買っている（中学校で習う『切片』）」と解釈することができます。この「1%増えるごとにいくらずつ」という「傾き」の部分が第4話の中でも報告された「回帰係数」という指標になります。

　読者の中には、この「直線をあてはめる」「説明変数が１増えるごとの購買金額の変化量を一定と仮定する」というところに疑問を持つ方もいるかもしれません。実際に土曜日の割合が1～9％ほどのお客さんは、土曜日の割合が0%のお客さんよりむしろ購買金額が低くなっているので、「1%増えるごとに1000円ずつ高い」というのはあまり正しくないようにも見えます。

　せっかく高校で二次関数というより高度な数式を習うのだから、そちらで当てはめた方が正確な予測になるのではないでしょうか？　実際やってみるとこのデータに対して次のようにきっちりフィットします。

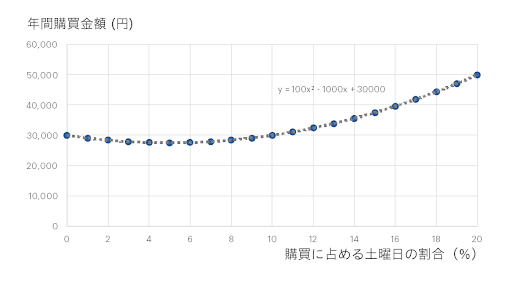
　しかし、その一方で「要するにどうしたらいいか」と説明するのはだいぶ難しくなってしまいます。「y=100x^2-1000x+30000という数式でピッタリ当てはめることができました」と言われても、結局のところ、その説明変数x（土曜日の割合）が高い人を狙った方がいいのか、低い方の人を狙った方をすぐに判断できる人は、限られた数学の得意な人だけになってしまうでしょう。

　物理や工学の研究であれば「最適な数値にうまくコントロールする」という精密な制御が可能ですが、人間を対象にした分析結果では、「結局のところその説明変数を大きくした方がいいのか小さくした方がいいのか」という程度のアクションしかとれません。それであれば最初から「直線であてはめるものとする」という仮定を置いて、直線の傾きを示す回帰係数がプラスなのかマイナスなのか、だいたいどれくらいの値なのか、と考えた方が有益です。これが、線形回帰モデルがビジネスに限らず、医療や教育などさまざまな現象を理解するためによく用いられる大きな理由です。

　また、単回帰分析をふくむ線形回帰モデルは、「大きい方がいいか小さい方がいいか」だけなく、「どの状態になることがいいのか」が知りたい場合にも使うことができます。
　この場合、「何かのカテゴリーに該当する場合は1, しない場合は0」という変換を行えばOKです（このような0か1かに変換したものをダミー変数と呼びます）。たとえば「女性なら1、男性なら0」と変換したものは「女性ダミー」と呼ばれたりしますが、この説明変数だけで行った単回帰分析は次のようなイメージになります。

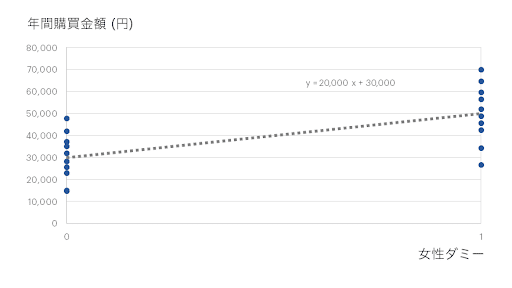
　こちらは数式で言うと、

購買金額　＝　20000　×　女性ダミー　＋　30000

すなわち回帰係数（傾き）が2万で、切片が3万という結果になっています。つまり、「女性ダミーが０」である男性においては平均3万円の購買があり、「そこから女性ダミーが1増えると購買金額が2万円増える」という回帰係数が得られ「女性はほかのカテゴリー（男性）と比べて購買金額が2万円高い」ということになります。こうすれば数量的ではない説明変数についても「どのような状態になるといいのか」を線形回帰モデルで捉えることができるのです。

重回帰分析：そのパワフルさと注意点

　さらに、「何かの説明変数が1増えるごとの、アウトカムの変化量は常に一定だったとしよう」という仮定はそのままに、「説明変数は単数とは限らず、複数あってもよいことにしよう」と拡張した線形回帰モデルは一般に重回帰分析と呼ばれます。たとえば次のような状況を考えてみましょう。

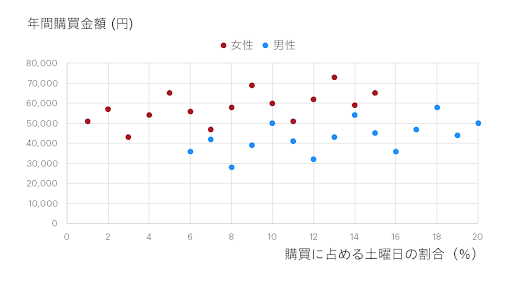
　比較的女性は左側（すなわち土曜日）に来る割合が低く、男性の方が土曜日に来ている割合が高くなっています。また、グラフを見れば何となく女性の方が、土曜日の割合が同じだとするとたくさん買ってくれていそう、という状況が見て取れます。一方、同じ性別だと土曜日によくきてくれている人がたくさん買ってくれそうです。

　しかし、男女間で土曜日の割合に偏りがあるため、単回帰をしただけでは土曜日の割合が大事なのかどうか、判断しにくくなっています。重回帰分析が役に立つのはこうした状況です。

　「何かの説明変数が1増えるごとの、アウトカムの変化量は常に一定だったとしよう」という線形モデルの仮定を、複数の説明変数を同時に含んだ状態に拡張する――これをグラフにすると、次のようなイメージになります。

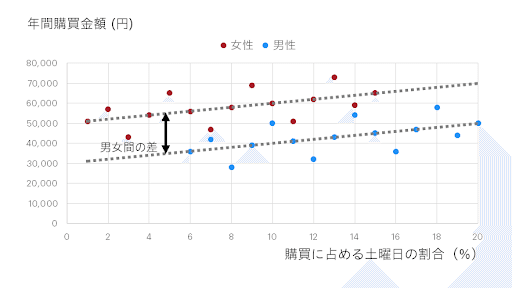
　つまり、「同じ性別だったら土曜日の割合が1増えるごとの購買金額の変化量は常に一定だとしよう」、あるいは逆に「土曜日に来る割合が同じだったとしたら、男女間での購買金額の差は常に一定だとしよう」と考えるわけです。そうすると、ズレが小さくデータのあてはまりがよいように、男女それぞれ同じ傾きの直線を平行に引くことができます。この平行線は数式でいうと次のように表すことができます。

購買金額
　＝　30000　＋　土曜日の割合　×　1000　＋　女性ダミー　×　20000

　説明変数とは無関係な「30000」という数値が切片と呼ばれることは単回帰分析と変わりません。また、土曜日の割合が1増えるごとに1000円ずつ購買金額が高い傾向にある、というのも、女性はほか（男性）と比べて20000円購買金額が高い、というのも同じく回帰係数と呼ばれます。

　さらに、このように「複数の説明変数を一気に分析できる」という重回帰分析の特徴と、ダミー変数の考え方を組み合わせると、「何かの説明変数が1増えるごとの、アウトカムの変化量は常に一定だったとしよう」という制約を緩和させることもできます。
　たとえば「年齢」という説明変数をそのまま使うと線形モデルでは「1才増えるごとにに購買金額はどれぐらい高くなる/低くなる傾向にあるか」という答えしか得られません。しかしながら、20代から30～40代にかけてはビールの消費量があがっていくものの、50代～60代にかけて徐々にあまりビールを飲まなくなる、といった状況であれば「1才増えるごとに購買金額がどう（直線的に）変わるか」という結果はあまり参考にならないかもしれません。

　しかし、年齢という説明変数を「年代」という複数のダミー変数に置き換えた上で重回帰分析を行うことでこの問題は回避できます。「女性かそれ以外の性別（すなわち男性）か」とダミー変数を考えたように「30代かそれ以外の年代か」「40代かそれ以外の年代か」というように複数のダミー変数を考えれば、重回帰分析の仮定は「年代の違いによる購買金額の差は一定だったとしよう」というものとなり、特定の年代だけで購買金額が高いとか低いといった分析結果を得ることもできます。実際に勇司が報告した分析結果でも「30代と40代だけが購買金額が高い」という結果が得られていました。

　このように重回帰分析を使えば、十分な件数のデータがある限り、いくらでも説明変数を増やすことができます。しかし、説明変数を増やせば増やすほどいい結果になる、というわけではありません。
　たとえば先ほど平行線を引いたようなデータでは確かに男女間の差は考慮した方がよさそうでしたが、実際に男女間でまったく買い方に違いはないはずの商品であっても、「ちょうど男女間の購買金額の平均値がぴったり一致する」というわけではないのです。このような状況では、ある期間のデータではたまたま女性の方が少し多めに買っていたが、また別の期間のデータではたまたま男性の方が少し多めに買っている、という一貫性のない重回帰分析の結果が得られることだって十分あります。
　つまり、実際には意味のない説明変数を回帰モデルに含めてしまったために、むしろアウトカム（購買金額）の予測精度が下がるリスクも考えられるわけです。

　そんなわけで第４話で報告していた分析結果を得るために貴子が用いたのが「変数選択」という技術でした。

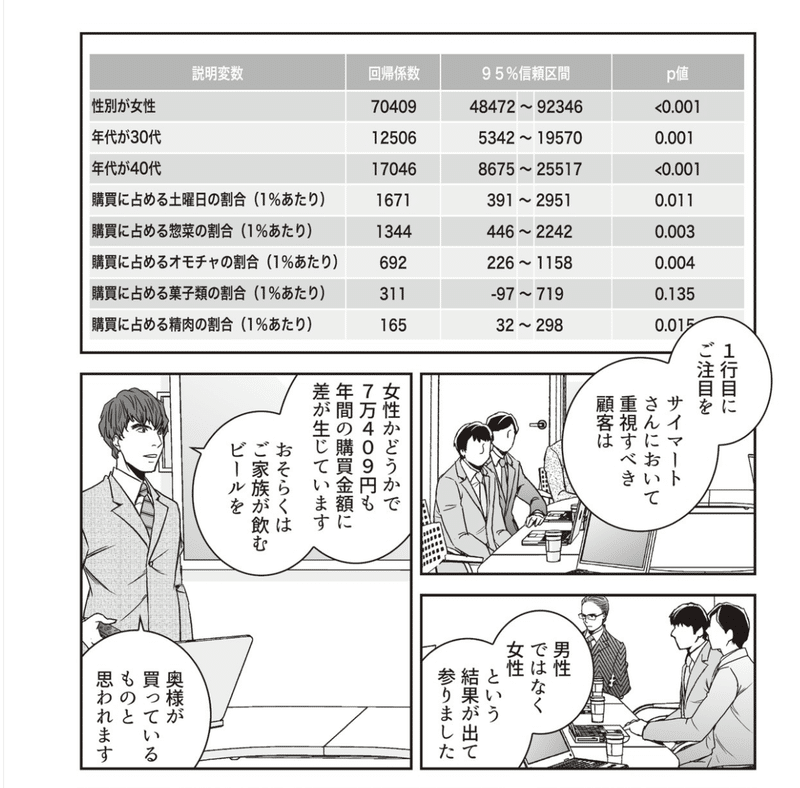
　データから可能な限り大量の説明変数の候補を定義したのちに、安定して予測精度（つまりモデルから予測されるアウトカムの値と実際の値のズレの小ささ）の向上に繋がるような説明変数はモデルに含め、そうでない説明変数はモデル削除する。そうした変数選択を自動化するための手法は統計学者によっていくつも提案されています。

　勇司と貴子はこのように重回帰分析によって得られた統計モデルによって、求めるアウトカム（購買金額）に対して、何の説明変数がどれくらい関係しているのかを発見することができました。

　もちろん倉田課長も「相関と因果は違う」と指摘したように、「関係している」からといって、本当にその説明変数の条件を変えたり、説明変数の条件を満たす人を狙ったりするアクションによってアウトカムが改善するかどうかは断言はできません。しかしだからといって、「慎重に議論」したからといってもそれは同様なのです。

　そんなわけで次回の補足コラムでは、なぜ貴子の言うランダム化比較実験が回帰モデルから一歩踏み込んで、「関係している（相関）」ではなく「影響している（因果）」ことの検証になるのかについて説明したいと思います。