ラジアンが教えてくれたものって話。

高校時代に三角比と三角関数をとことん曖昧にしたままだったのがこの15年ほどずっと心残りで、今復習してる。

そんな中で、ラジアンに再会した。

ラジアンとは角度の表し方の一つで、「半径を1とする扇形の弧の長さが1になるときの中心角の大きさを1ラジアンとする」というものだ。三角比・三角関数は直角三角形の直角以外の二角の大きさと、それに対応する辺の長さの比がそもそもの問題の始まりなので、「角度」がとても重要なのだ。ラジアンについて以下で少し説明する。

基準となる線を「始線」、始線と角度を作る線を「動径（どうけい）」と言う。

この時の角度θ（シータ）をどうやって測るか？
こう聞かれると、ほとんどの人が始線に分度器を当てて動径の角度を測ろうとするだろう。これは、1°という角度の大きさを基準に、θが何度になるかを直接計測するやり方だ。

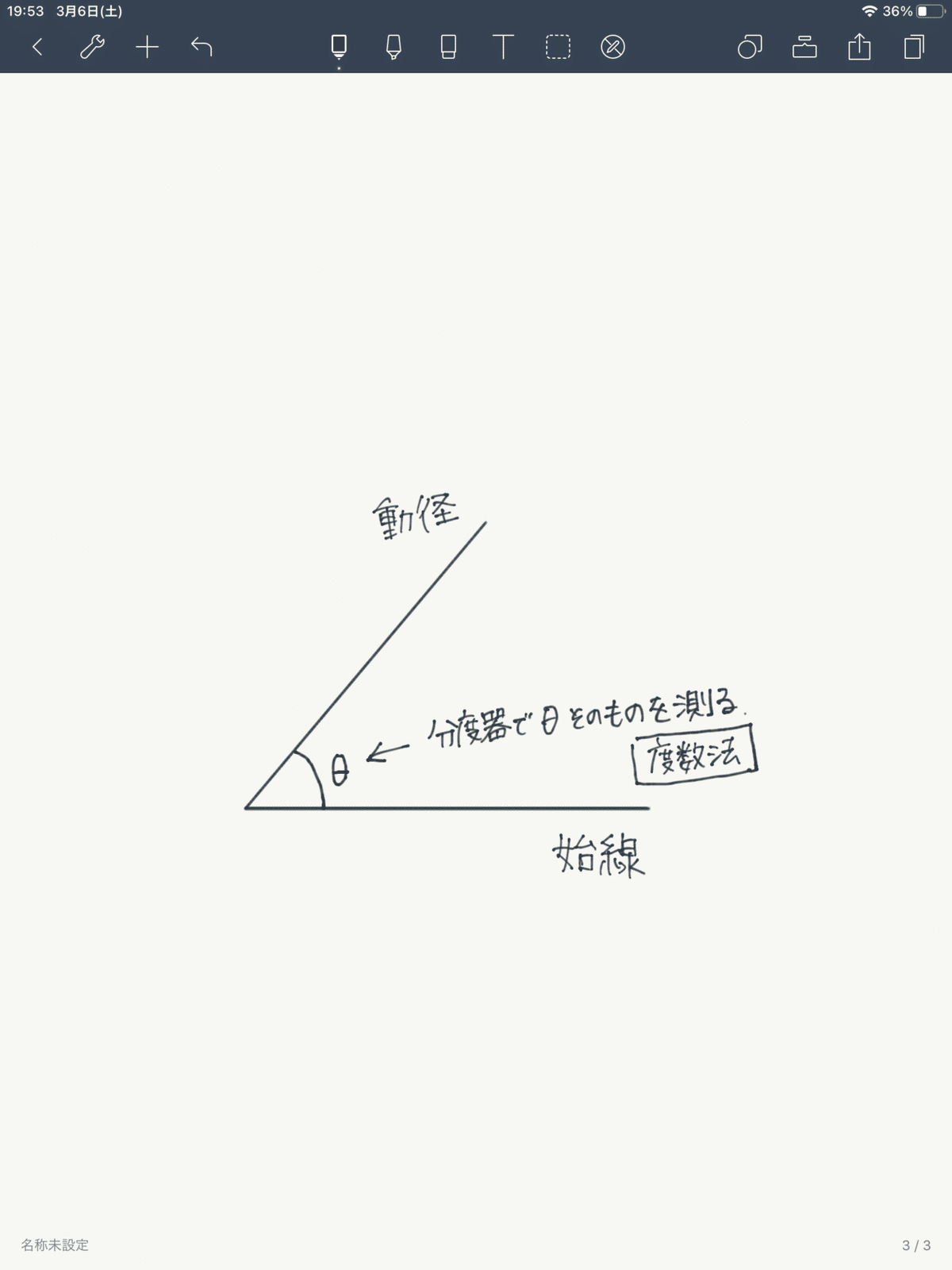
それに対して、もっとトリッキーな角度の測り方がある。弧度法と言われるもので、これが冒頭のラジアンと関係してくる。ラジアンは弧度法での角度の単位だ。弧度法では、始線と動径に分度器を当てて角度を直接測るのではなく、始線と動径が作る扇形の弧の長さに注目する。

その時、始線の長さを1とするのが約束である。

弧度法では、角度そのものではなく、扇形に注目して角度を定義する。度数法とは見ているポイントが微妙に違う。

度数法で1°という基準があるように、弧度法にも1ラジアンという基準がある。1ラジアンは、半径1の扇形の弧の長さが1になる時のθの大きさということになっている。文字にするとなんだかわかるようなわからないような感じだが、図にすると割と入ってくるかもしれない。こんな感じだ。

角度なのに10°とか20°とか言わないのでなかなかピンとこないかもしれないが、これも立派な角度の測り方である。

この2つの角度の測り方は互いに換算可能である。同じものを測っているので当然と言えば当然だけれど。換算については、角度が180°になる時を考えるといい。結論から言うと、

180°＝πラジアン（だから、1°＝π÷180 でもある）

になる。πはギリシャ文字のパイ。πを「円周率」として覚えている人も多いはず。こんなところでなぜπが？と思ってしまうかもしれないが、これには立派に理由がある。というか、「円周率＝円の直径に対する円周の比率」というところから必然的にこうなることになっている。

弧度法では始線と動径が作る扇形の弧を考えるので、180°の時は、扇を完全に開き切った形になる。そして、半径を1としているので、始線と動径が一直線になるとき、その長さは2であり、これは円の直径と同じになる。その時の弧は当然円周の半分の長さになるはずなので、計算するとその長さはπになるのだ。

度数法で測った角度180°は、弧度法のπラジアンと同じ大きさなのである。ここから、1°＝π÷180ということもわかるので、結局どんな角度であっても〇〇°と表記することもできるし、△△ラジアンと弧度法で表記することもできる。度数法と弧度法は測り方こそ違うものの、互いに換算可能で同じものを違う方法で見ているということがわかる。

ちなみに、これは高校数学の内容なので、数学IIの授業を受けている人なら知っているはずのことだ。僕ももちろん受けたので、ラジアンとかはなんとなくでも覚えていた。

ただ、ぶっちゃけた話、ラジアンのことを詳しく知らなくても、三角関数の中でπが出てきたら180°と考える！と暗記しているだけで大抵の問題は解けるのだ。僕も高校生の時はそのようにただ単純に覚えていて、ラジアンのことをそこまで深く考えたことはなかった。

でも、今三角関数の復習をしていて、うろ覚えだったラジアンに触れてなんかちょっと感動した。

角度を測ると言えば、誰もがまず角度そのものを測ろうとするだろう。それが人情というものだ。でも、弧度法は違う。角度そのものではなく扇形の弧の長さを測ろうとする。一見ゴールに直接結びついていないものの、数学において非常に重要な数であるπを使って角度を表現することに成功している。

このやり方はとてもクリエイティブだと思う。角度がどーのこーのということではなく、ある事柄に対する考え方は、「色々あるはずだ」ということを教えてくれている。

一つの方法で行き詰まっても、他に突破口があるかもしれない。こちらのルートよりも別なもっとシンプルなルートがあるかもしれない。これって、まさに数学の問題を解く時によく考えていたことだ。

40年も生きると、自分の能力の限界とか得意不得意などいろんなことがわかってしまうこともある。それでも、もっと違うやり方ならば、同じものをそれこそ違う角度から眺めたら、自分にもアプローチ可能な方法で取り組めるようになるかもしれない。

こんなことはもう言い古されて改めて書くのも恥ずかしいくらいのことだが、なんか今日は改めてそう思って、まだこれから色々頑張れるかもしれないな、と感じた次第でございます。

んじゃね！