インバージョンの基礎理論②～最小二乗法～【私の備忘録】

　前回のインバージョンの基礎理論①では，インバージョンの概要とインバージョンを理解する上で必要な数学的な知識について説明しました．本回では，一番基本的なインバージョンである最小二乗法(LSM: Least Squares Method)の計算法について数学的に説明していきます．今回は，コンピューターによる数値計算を視野に入れ，行列を用いた最小二乗法の計算法について説明していくことにします．
※大学初級レベルの基本的な数学(特に線形代数学)を使います．必要な公式については前回の記事を参照願います．

最小二乗法とは

　最小二乗法とは，観測データ全てに対して直線の方程式で近似するという方法です．例として，表1のように，年齢と身長の関係を考えてみましょう．年齢をx軸，身長をy軸にとります．

表1　年齢と身長の関係

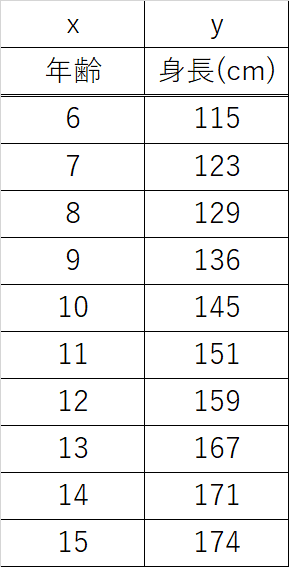
年齢(x軸)と身長(y軸)は直線の関係に近似できると仮定すると，図1のように直線の方程式(y=ax+b)で近似できます．この直線は，観測値との差が最小になるようなa, bを求めることで決めることができます(図2)．このa,bが未知数(最小二乗法で求めたいモデル)です．

図1　最小二乗法による身長と年齢の直線近似

図2　最小二乗法による直線近似のイメージ

最小二乗法による未知数の決定法

　観測値ti (i=1,2,3)が(2-1)のような線形方程式で近似できるとします．ここで，x1, x2が最小二乗法によって求めたいモデル(未知数)，a11,a12,・・・は係数です．

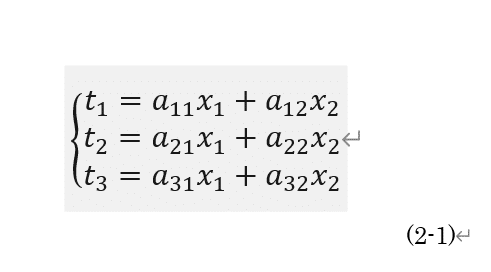
次に，ヤコビアン行列Aを求めます．ヤコビアン行列の要素は(2-2)のように表せます．

(2-2)より，ヤコビアン行列は(2-3)と表せます．

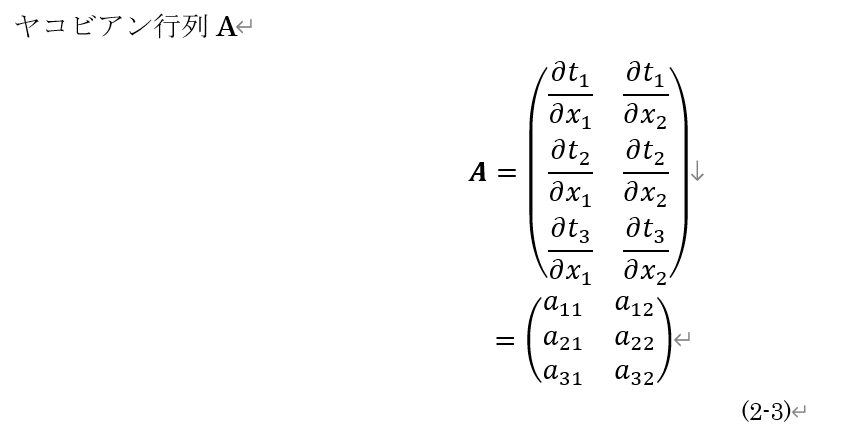
以上から，(2-1)は，ヤコビアン行列A，未知数ベクトルX，観測値ベクトルTを用いて(2-4)のように表せます．

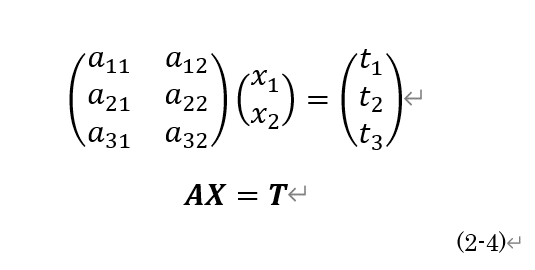
次に理論値と観測値との差(残差)を求めます．残差ベクトルをeとすると，(2-5)のように表せます．ここで，観測値ベクトルをYと置き換えます(行列の転置の記号をTと表したいので，便宜的に観測値ベクトルをYに置き換えることにします)．(2-5)で，第1項のAXが理論値，第2項のYが観測値となります．

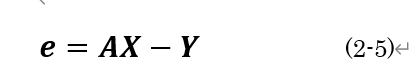
最終的に，残差が最小になるときのXを求めたいので，残差二乗和が限りなくゼロに近づくときのXを求めることを考えます．つまり，残差二乗和を未知数Xで偏微分した結果が0になるときのXを求めることを最終目標とします．残差二乗和をEとすると，(2-6)のように表せます．

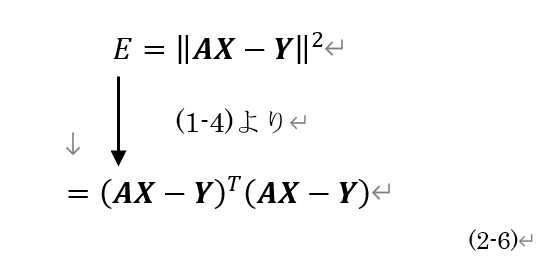
(2-6)を展開すると，(2-7)のように表せます．

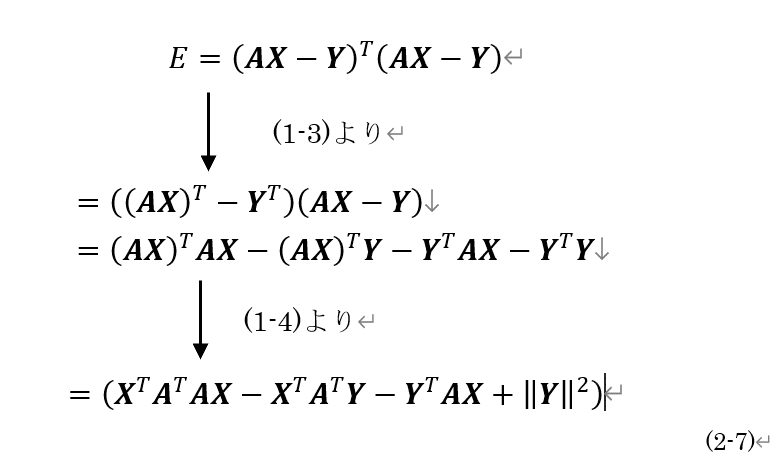
ここで，(2-7)を未知数Xで偏微分することを考えます．偏微分は，第1項，第2項・第3項の2つのかたまりに分けて計算したほうがわかりやすいです．
まず，第1項の偏微分は，(2-8)のように計算できます．

続いて，第2項・第3項の偏微分は(2-9)のように表せます．

以上より，(2-7)全体の偏微分は(2-10)のように表せます．

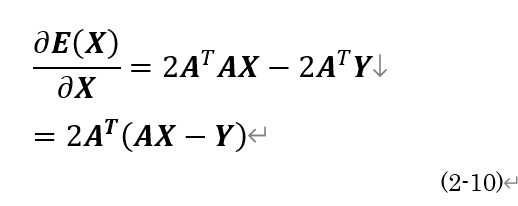
(2-10)がゼロになればよいので，

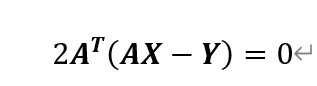
となります．これを整理すると，(2-11)のように表せます．

(2-11)を解くべき正規方程式(Normal Equation)といいます．
(2-11)をXについて解くと，(2-12)のような結果となります．

(2-12)によって，未知数(求めたいモデル)X=(x1,x2)を求めることができます．

 　以上が最小二乗法によって未知数を求める方法です．次回は，非線形最小二乗法(Non-Linear Least Square Method)について説明致します．非線形最小二乗法は地球物理学的観測データの逆解析で最もよく使われる手法です．

補足として，逆行列の性質を示しておきます．