【アッセイを考える #3】ミカエリス・メンテン式の拡張

　「アッセイを考える」シリーズの3回目である。前回は、細胞外では働くが細胞内では働かない酵素の謎に迫り、細胞という区画化された環境がもたらす特殊な状況を紐解いてきた。

　今回の題材は細胞を一旦離れ、酵素に着目してみることとする。

【問題3】
　酵素Aは以下の反応を触媒することが知られている。

$$
S_1 + S_2 → P_1 + P_2
$$

　この酵素がミカエリス・メンテン式に従う時、速度論的パラメータ（$${K_{m,S_1}}$$：$${S_1}$$に対するミカエリス定数、$${K_{m,S_2}}$$：$${S_2}$$に対するミカエリス定数、$${k_{cat}}$$：分子活性）を求めたい。どのような実験を行うのがよいだろうか。

【回答例】
　教科書では1基質の反応がよく扱われているが、特に代謝酵素を扱う場合なんかは、2基質以上の場合が圧倒的に多いと思う。文献などを紐解いてみると、過剰に存在する基質（NAD(H), NADPH, ATP, O2 …）の濃度を固定した上で、もう一方の基質の濃度に対するミカエリス・メンテン式を解くことが多い。

　もし、上記のような状況ではないとすると、2基質の酵素反応を真面目に考えることになる。2基質の酵素反応を調べてみると、その反応機構には様々な種類があってややこしい。酵素Aがどのような機構で反応を触媒するか、前提知識を持っていないことも多い。ただ、酵素反応機構がどんなものであれ、1つの統一した式で説明できることが知られている。

2基質の酵素反応の一般式

$$
[E] / V_0 = Φ_0 + Φ_1 / [S_1] + Φ_2 / [S_2] + Φ_{1,2} / ([S_1][S_2])
$$

$${[E]}$$：酵素濃度
$${V_0}$$：反応初速度
$${[S_1]}$$：$${S_1}$$の濃度
$${[S_2]}$$：$${S_2}$$の濃度
$${Φ_0, Φ_1, Φ_2, Φ_{1,2}}$$：速度論的パラメータ

　ここで、$${K_{m,S_1} = Φ_1 / Φ_0, K_{m,S_2} = Φ_2 / Φ_0, k_{cat} = 1 / Φ_0}$$ であるから、$${Φ_0, Φ_1, Φ_2, Φ_{1,2}}$$ を求めることができれば、問題に回答できる。酵素反応の一般式に於いて $${[S_1]}$$ を変数に見立てることで、以下のように書き換えられる。

$$
[E] / V_0 = (Φ_0 + Φ_2 / [S_2]) + (Φ_1 + Φ_{1,2} / [S_2])・(1 / [S_1])
$$

　特定の $${[E]}$$ に於いて、$${[S_1], [S_2]}$$ を振った時の $${V_0}$$ を記録していくと、以下のようなグラフを描くことができる。

引用元：Initial Rate Kinetics of Multi-Substrate Enzymes

　このグラフの各回帰直線における傾き（$${= Φ_1 + Φ_{1,2}・(1 / [S_2])}$$）と切片（$${= Φ_0 + Φ_2・(1 / [S_2])}$$）をそれぞれ計算した上で、$${1 / [S_2]}$$ に対してプロットすることで、$${Φ_0, Φ_1, Φ_2, Φ_{1,2}}$$ をそれぞれ求めることができるわけだ。下図で言えば、Intercept の回帰直線の傾きが $${Φ_2}$$、切片が$${Φ_0}$$であり、Slope の回帰直線の傾きが$${Φ_{1,2}}$$、切片が$${Φ_1}$$である。

引用元：Initial Rate Kinetics of Multi-Substrate Enzymes

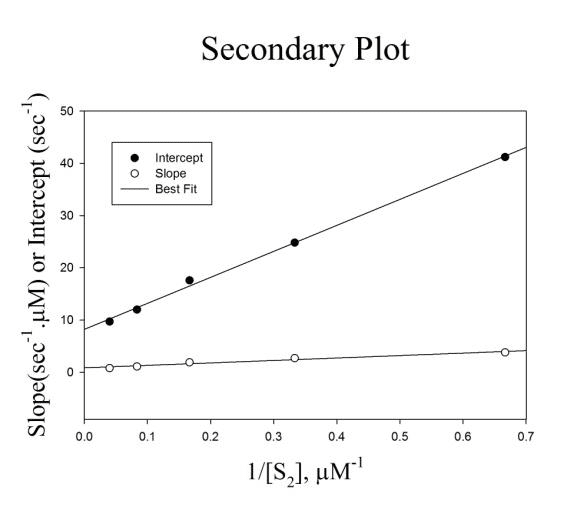
【要点】
　合成生物学の中でも、酵素工学の分野で大事になる考え方である。酵素の性能を高めるためには、そもそもの酵素の性能を正しく評価できていることが重要だ。２基質ともに濃度が決して大過剰ではない場合、理論に立ち返って考えてみよう。2基質の酵素反応速度論が1つの式で書き下せることは驚くべきだ。

【参考文献】
Initial Rate Kinetics of Multi-Substrate Enzymes