
Excelのソルバー機能の使い方~使用方法~ (練習問題の回答)
こんにちは!分析屋業務効率化チームのWです!現在は、皆様の業務効率化のお手伝いや、ExcelのVBAを用いたツール作成などを行っています。
前回の自分noteでは、Excelのソルバー機能をオンにする方法と練習問題をご紹介しました。
今回は、出題した練習問題の解答とソルバー機能の使い方をご説明していきます!
問題1
ある工場では、2種類の商品 (AとB) を製造しています。
それぞれの商品を製造するためには、異なる材料と時間が必要です。
利益を最大化するためにこれらを考慮して計画を立てる必要があります。
1日で最大の利益を出すためには、AとBをどれだけ作ればよいでしょう?

製品Aを作る数を$${X_a}$$個、製品Bを作る数を$${X_b}$$個とします。
問題の考え方として、まず目的関数(求める値)を考えていきます。問題1では最大の利益を出すことを求めているので、Aを作る時の利益とBを作る時の利益の合計が最大となるのが目的関数となります。式にすると$${2000X_a + 3000X_b }$$→最大 となります。
続いて、目的関数を出す時の制約条件を考えていきます。問題1では時間と材料がそれぞれ制約条件となっていることが分かります。それぞれを式でまとめると、時間:$${2X_a + X_b≦ 24 }$$材料:$${3X_a + 4X_b ≦30}$$ となります。
出てきた式をまとめると、以下になります。
目的関数:$${2000X_a+ 3000X_b}$$ →最大
制約条件:$${2X_a + X_b≦ 24 }$$・・時間
:$${3X_a+4X_b ≦30}$$・・材料
制約条件を満たし、目的関数が最大値となる$${X_a}$$ と$${X_b}$$を探すと、$${X_a}$$は2個、$${X_b}$$ は6個となり、この時の利益は22,000円となります。
ここまでを手動で計算する場合、$${X_a}$$が1の時、$${X_b}$$が2の時...とすべてを計算する必要があるのですが、少し面倒ですよね!なので、ソルバーを使って代わりに計算してもらいましょう!
ソルバーの使い方
①問題1の表に合計欄を用意
問題1と同じような表を作成し、合計の欄を追加してください。

②合計の行に計算式を入れる。
時間にはA,Bを作成するときの合計時間を計算する式を入れます。同じように材料にはA,Bを作成するときの合計使用材料、利益には合計利益を計算する式を入れます。
これらは、B8が$${X_a}$$、B9が$${X_b}$$の値として変化するときに、どの程度の値を取るかを計算するためです。
試しにB8に1、B9に4と入力すると、合計の6がB4に表示され、合計で6時間かかることを表しています。

③Excelのリボンタブ「データ」からソルバーを選択
ソルバーを選択すると以下のように、ソルバーを設定する画面が出てきます。

④目的セルと目標値、変数セルを設定
目的セルには、求める値のセル番号(利益の合計)を入力してください。目標値は、利益の最大を目指すので「最大値」を選択。変数セルには、決定変数のセル番号(A,Bの作成量)を入力してください。
ソルバーでは、この変数セルの値を変化させて目的値を探索しています。手計算で行う場合の$${X_a}$$が1の時、$${X_b}$$が2の時...の部分です。

⑤制約条件を設定
制約条件を設定していきます。最初にまとめていた時間と材料の制約条件を入力してください。また、時間と材料の制約条件を入力しただけでは、変数セルに小数点が含まれた解答がでてきてしまいます。今回は整数の解答を求めるので、「変数セルが整数」という条件も加えます。

※制約条件の部分には値だけでなく、セル番号も入力できます(今回だとB5)
「変数セルが整数」という条件は「≦」の部分を「int」にすることでできます。

⑤ソルバーの解決ボタンを押下
解決ボタンを押すと解答が出てきます。最終的に以下の画像のようになれば成功です。

ソルバー機能はいかがでしょうか?まだ問題が簡単なので、Excelの枠を作成していくよりも手計算の方が早いという方もいると思います。なので、もう少し条件を加えた問題2を考えていきましょう!
問題2
ある工場では、2種類の商品 (AとB) を製造しています。
それぞれの商品を製造するためには、異なる材料と時間が必要です。
また、受注注文があり商品ごとに最低限製造する必要があり、製造可能数も決まっています。
各製品の製造にはコストがかかり、利益を最大化するためにこれらを考慮して計画を立てる必要があります。
一日で最大の利益を出すためには、AとBをどれだけ作ればよいでしょう?
※分かりやすくするため、前回と問題文と表を少しだけ変えています。条件は変わっておりません。
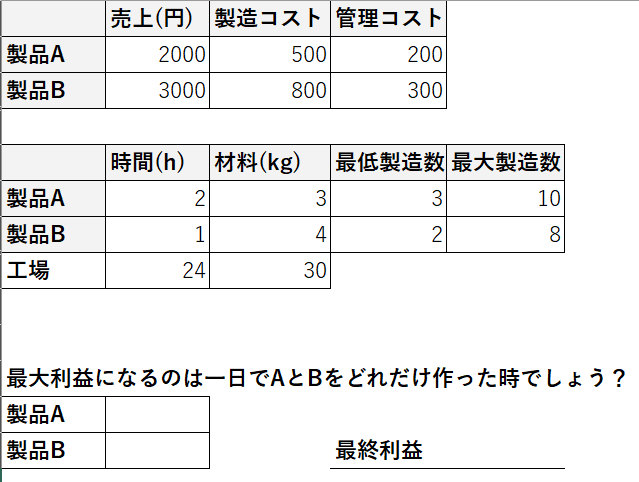
製品Aを作る数を$${X_a}$$個、製品Bを作る数を$${X_b}$$個とします。
まずは目的関数を考えていきます。今回は利益のほかに、製造コストと管理コストがかかっています。これらを含めて式を作ると$${(2000X_a + 3000X_b ) - (500X_a + 800X_b) - (200X_a + 300X_b)}$$ →最大 となります。
続いて制約条件を考えます。問題1より追加された条件は最低製造数と最大製造可能数です。これらを考えると、製造数の条件式は$${ 3≦X_a≦10、2≦X_b ≦8}$$となります。
問題1でまとめた式と、問題2で新たに追加された条件式をまとめると以下になります。
目的関数:$${(2000X_a + 3000X_b ) - (500X_a + 800X_b) - (200X_a + 300X_b)}$$ →最大
制約条件:$${2X_a + X_b ≦ 24}$$・・時間
:$${3X_a +4X_b ≦30}$$・・材料
:$${3≦X_a≦10}$$・・製品Aの製造数
:$${2≦X_b ≦8}$$・・製品Bの製造数
これらをソルバーを使って解いていきましょう!
問題2のような表を用意し、以下のように合計の行を追加してください。
最終利益には製造コストと管理コストを含めた式を入力します。

続いて、ソルバーには以下のように制約条件を設定します。

最終的な解答としては、$${X_a}$$は6個、$${X_b}$$ は3個となり、この時の最終利益は13,500円となります。
まとめ
以上でExcelのソルバーを使った練習問題は終了です!練習問題のように、Excelのソルバーを使えば簡単な最適化問題を解くことができます。使う機会は少ないかもしれないですが、便利な機能なので、ぜひ覚えておいて下さい!
ここまで読んでいただきありがとうございました!
ここまでお読みいただき、ありがとうございました!
この記事が少しでも参考になりましたら「スキ」を押していただけると幸いです!
他のEXCEL便利機能の記事はこちら!
株式会社分析屋について
弊社が作成を行いました分析レポートを、鎌倉市観光協会様HPに掲載いただきました。
ホームページはこちら。
noteでの会社紹介記事はこちら。
【データ分析で日本を豊かに】
分析屋はシステム分野・ライフサイエンス分野・マーケティング分野の知見を生かし、多種多様な分野の企業様のデータ分析のご支援をさせていただいております。 「あなたの問題解決をする」をモットーに、お客様の抱える課題にあわせた解析・分析手法を用いて、問題解決へのお手伝いをいたします!
【マーケティング】
マーケティング戦略上の目的に向けて、各種のデータ統合及び加工ならびにPDCAサイクル運用全般を支援や高度なデータ分析技術により複雑な課題解決に向けての分析サービスを提供いたします。
【システム】
アプリケーション開発やデータベース構築、WEBサイト構築、運用保守業務などお客様の問題やご要望に沿ってご支援いたします。
【ライフサイエンス】
機械学習や各種アルゴリズムなどの解析アルゴリズム開発サービスを提供いたします。過去には医療系のバイタルデータを扱った解析が主でしたが、今後はそれらで培った経験・技術を工業など他の分野の企業様の問題解決にも役立てていく方針です。
【SES】
SESサービスも行っております。
