麗しのコーヒー　その１

コーヒーなどのドリンク類による癒やしは、味や香りに因るものだけでなく液体の動きというビジュアル面にも起因していると思う。気付いたらコーヒーの動きを眺めていることが度々ある。人間の感性と液体の挙動は相性がよいのかもしれない。そう感じるのは私だけかもしれないが。

まずは角砂糖を落とすような場合から、カップの中のコーヒー表面の動きを再現してみたい。

基本的に計算方法は
　波紋を思い描く　その１
　波紋を思い描く　その２
　波紋を思い描く　その３
　波紋を思い描く　その４
と同じ。とくにその１、その２までは全く同じだ。違いはその３の境界条件のみであるので境界条件から考える。

shixugang, pixabay.com

境界条件

　波紋を思い描く　その１
　波紋を思い描く　その２
の続きをマグカップで考える。

Fig.5

カップの半径を$${r_a}$$で一定とする。カップの壁面でr方向の速度は0になるので

(46)

(45)より

(47)

となればよい。 (39)を用いて

(48)

となるので、Bessel関数を微分して0になる点を見つければよい。
n次のBessel関数の微分の正のm番目の零点を$${λ_{m,n}}$$として分離定数$${α_{m,n}}$$は

(49)

となる。次数nだけでなくBessel関数の微分の零点の番号を表すmが新たに追加される。これは径方向の波の重ね合わせに相当する。

(39) (44) (45) (49)より速度ポテンシャルは

(50)

となる。

時間成分

(17)をtで微分して

(51)

ηの時間微分はz方向の速度なので

(52)

(20)を代入して

(53)

Zは既知であるので(50)より

(54)

となる。
ここで変位ηは水底から基準位置までの高さHと比べて十分小さいとする。また高さ(深さ)は一定とする。

Fig.6

(55)

(54)に代入して

(56)

となる。

(57)

を用いて

(58)

であるので$${T_{m,n}}$$​を以下とする。

(59)

ここで(17)より

　(60)

(55)よりzをHに固定して、 (50) (59)を(60)に代入する。

(61)

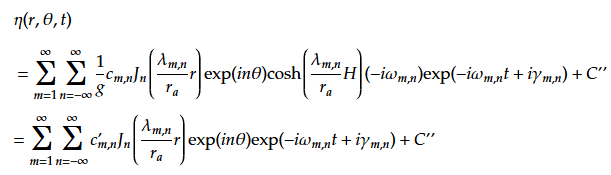
tで微分して

(62)

t=0において変位は初期条件である形状を持たせ、変位方向の速度は簡単にするため0としたい。

(63)

よって位相の初期値は0となる。

(64)

以上より

(65)

となるので係数$${c'_{m,n}}$$および定数C''が決まれば、位置(r,θ)および時間tを指定することで変位ηが求まる。

その２に続く