結び目理論超入門(凝縮系物理に関わる結び目理論)【論文紹介】#21
まず、結び目理論の入門として、ありそうな誤解を一つ解いておく(私がしばらく誤解していたことだが)。
結び目理論は、3次元空間中の結び目そのものを扱うのではない。結び目を2次元平面に描いた結び目図式とそれに対する操作のみを扱う(下図A)。一旦2次元に落とすために、やや回りくどいことをやっているようにも見えるが、2次元に落とすおかげで扱いやすくなっているという恩恵は大きい。
本記事では、結び目不変量(同じ結び目なら同じ値、違う結び目なら違う値になるもの)の代表例である、ジョーンズ多項式の理解までを目指す。(本記事ではわかりやすさのためにやや厳密さを欠いた表現がありますがご了承ください。)
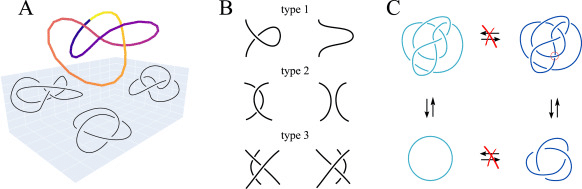
B. 3つのライデマイスター移動
C. アイソトピックな移動(上下方向)とそうでない移動(左右方向)
結び目を2次元平面に書き写す結び目図式は、正確に扱えるように次のような書き方のルールがある。
・線は常に連続で、途切れたり折れ曲がったりしてはならない。
・線に端はなく、閉じたループになっていなければならない。現実の結び目でよくある、端が何らかの別のところに固定されていたりブラブラしているものも、両端が無限遠点でつながっているものとみなしてから、有限の大きさのループに描く。
・線の交点は2本だけの交差でなければならず(3本以上が1点で交わる点はあってはならない)、どちらが上を通るかを明確にしなければならない。(下を通ることを示すためにそこだけ途切れるように描くことが多い。)
3次元空間中で、結び目を切ったりすり抜けたりせず連続に変形できることをアイソトピック(isotopic)と言う。これは、はさみや接着剤を使わずに結び目を手で変形させる動作と同等な、至って現実的なルールである。アイソトピックな移動のみで移り変われる結び目は同じ結び目である。
2次元の結び目図式上では、アイソトピックな移動は上図Bの3種類のライデマイスター移動で全て記述することができる。この3つのライデマイスター移動は、3次元ではあまり考えなくてよいが2次元では発生してしまう交点についての変化規則である。
Type1, 2は交点が増えたり減ったりする(左右どちら方向への変化もある)。
Type3は2本が交差している下を3本目が通りすぎるのであるが、途中で3本が1点で交差する瞬間があり、それは2次元の結び目図式では特別な瞬間に見えるが、3次元ではなんてことはないのでこのルールでokとしている。(この図では2本の交差の下を通っているが、上や間を通る場合も同様。)
いわば、ライデマイスター移動は、2次元の結び目図式で見ると交点の数が変わるけど3次元ではどうということないアイソトピックな移動なのでやってよいというルールである(交点数を変えずに線の位置や長さを変える移動は自明とする)。そして3次元空間中で結び目がアイソトピックな移動をする時、2次元の結び目図式上での交点の変化の仕方はこの3タイプしかないので、この3つのライデマイスター移動だけで、全てのアイソトピックな移動を記述できる。(←これはかなり強力な定理!)
ここからは結び目不変量を考えるために、結び目図式Dに対してカウフマン括弧という、次のような記号と記号操作をまず導入する。
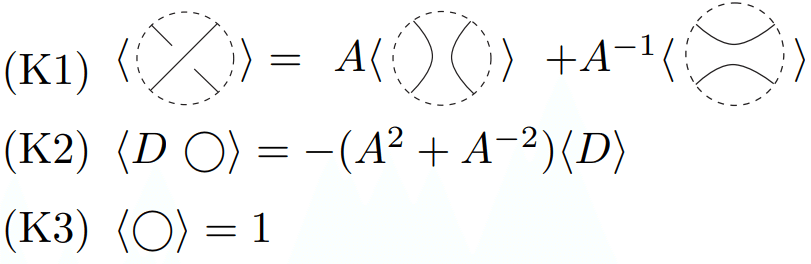
まずK1の左辺は、結び目図式の内の1つの交点に注目し(点線の丸の外は変えない)、その交点を切ってくっつけて交点をなくす操作を2通り(上下をつなげるものと左右をつなげるもの)考える。切ってくっつけるのはアイソトピックでない、ルールを逸脱する操作だが、その目印として$${A}$$と$${A^{-1}}$$を付ける。この$${A}$$は何かというと、ここでは抽象的な操作ひとつと思っておけばよい。この$${A}$$をもう少し加工すれば結び目不変量になることが後にわかる。
次にK2の左辺は、任意の結び目Dと孤立した輪があったら、右辺のように$${-(A^2+A^{-2})}$$という目印をつけて孤立した輪を無視する。1つのつながった結び目でも、K1の操作をしていくと孤立した輪が発生することがあり、その分は$${-(A^2+A^{-2})}$$という目印をつけて無視し、本体の結び目DをK1の操作でどんどん単純にしていくということである。
最後にK3は、K1, K2を繰り返して、本体の結び目Dが交点のない1つの輪(自明な結び目)になったらその値は1になって操作は終わりとなる。
試しに、最も単純な結び目である三葉結び目のカウフマン括弧の値を計算してみよう。
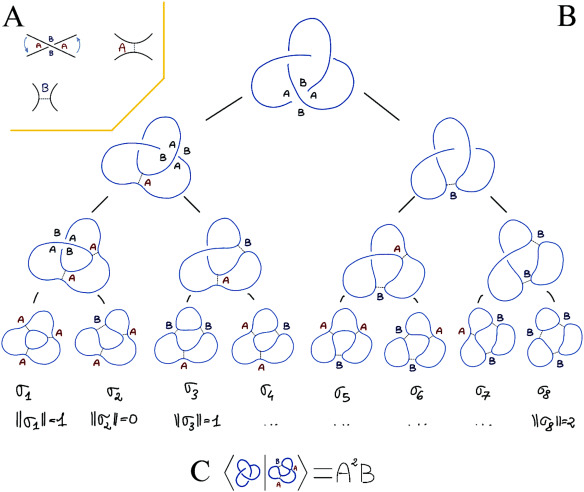
上図に対応して、それぞれ同じ段の〈 〉内に上図の結び目が入るとする。
$${〈 〉}$$
$${=A〈 〉+A^{-1}〈 〉}$$
$${=A{A〈 〉+A^{-1}〈 〉}+A^{-1}{A〈 〉+A^{-1}〈 〉}}$$
$${=A{A{A〈※1〉+A^{-1}〈 〉}+A^{-1}{A〈※1〉+A^{-1}〈 〉}}+A^{-1}{A{A〈 〉+A^{-1}〈※1〉}+A^{-1}{A〈※1〉+A^{-1}〈※2〉}}}$$
ここまでK1の操作を繰り返して、交点が一つもなくなった。※1のところは本体の他に孤立した輪が1つ、※2のところは輪が2つあるので、そこにK2を適用し、他は自明な結び目なのでK3を適用すると、
$${=-(A^2+A^{-2})[A{A{-A(A^2+A^{-2})+A^{-1}}+A^{-1}{-A(A^2+A^{-2})+A^{-1}}}+A^{-1}{A{A-A^{-1}(A^2+A^{-2})}+A^{-1}{-A(A^2+A^{-2})+A^{-1}(A^2+A^{-2})^2}}]}$$(↓( )を展開すると)
$${=-(A^2+A^{-2})[A{A{-A^3-A^{-1}+A^{-1}}+A^{-1}{-A^3-A^{-1}+A^{-1}}}+A^{-1}{A{A-A-A^{-3}}+A^{-1}{-A^3-A^{-1}+A^3+2A^{-1}+A^{-5}}}]}$$(↓+と-で打ち消し合うところを消すと)
$${=-(A^2+A^{-2})[A{A{-A^3}+A^{-1}{-A^3}}+A^{-1}{A{-A^{-3}}+A^{-1}{A^{-1}+A^{-5}}}]}$$(↓内側の{ }を展開すると)
$${=-(A^2+A^{-2})[A{-A^4-A^2}+A^{-1}{-A^{-2}+A^{-2}+A^{-6}}]}$$
$${=-(A^2+A^{-2})(-A^5-A^3+A^{-7})}$$
これが、三葉結び目のカウフマン括弧の値である。
ちなみに、注目する交点の順番を変えても、足し算と掛け算の交換法則のおかげで最終的な結果は同じになる。
カウフマン括弧の値が、これ以外の任意の結び目に対して不変量になるかどうかは、3つのライデマイスター移動に関してカウフマン括弧の値が不変かどうかを調べてみればよい。

中:TypeⅡの左辺のカウフマン括弧を取り、交点がなくなるようにすると右辺と等しくなる。
下:TypeⅢの左辺と右辺のカウフマン括弧を取ると同じ形になる。
カウフマン括弧は、TypeⅡ,Ⅲの移動の前後では不変だが、TypeⅠの移動の前後では値が$${-A^3}$$だけ違う。TypeⅠが他と何が違うのかを考えてみると(線をベルトと考えてみるとわかりやすいが)、"ねじれ"の増減も同時に起こっている。TypeⅡ,Ⅲではねじれは起こらない。このねじれの分$${w(D)}$$は、カウフマン括弧を適用する前の結び目D全体で次のように数値化できる。
$${w(D)=}$$(/が上の交点の数)-(\が上の交点の数)
(これはベルトで0と8の字を作ってみるとわかりやすいだろう)
そして、求めていた結び目不変量であるジョーンズ多項式$${V_D(t)}$$は、カウフマン括弧の値$${〈D〉}$$に対してねじれの数$${w(D)}$$の分$${-A^3}$$を掛ける補正を入れたものであり、次のような定義である。
$${V_D(t)=(-A^3)^{-w(D)}〈D〉|_{A^2→t^{1/2}}}$$
(最後の$${|_{A^2→t^{1/2}}}$$は、$${A^2=t^{1/2}}$$の関係でA を t に置き換えるのであるが、これは今後の利便性のためであり、置き換えず全てAの多項式で書いても不変量である。)
このジョーンズ多項式の値は、めでたくTypeⅠのライデマイスター移動でも変わらない値となる。ねじれの数$${w(D)}$$が変わらないTypeⅡ,Ⅲでも当然変わらない。なので、ジョーンズ多項式は結び目不変量である。
今回紹介する論文はこちら。
Topology in soft and biological matter
凝縮系と生物に関わる位相幾何学
main.pdf (sciencedirectassets.com)
本記事のここまでで概ね、本論文の2.2章までは解説できました(参考文献欄を除いた118ページ中13ページ!)。この続きは、シリーズものとして書くかもしれませんし、続きが出なかったら各自読んでくださいということにするかもしれません。
どちらにしても、結び目理論を全く知らない人にとっては2章が大きなハードルに感じると思うので、そのハードルを少しでも下げられたらこの記事を書いた甲斐はあると思います。
また、結び目理論の入門としてはこちらの文献もわかりやすいです。演習問題を解いてみれば、より理解は深まると思います。
H28-suzuki.pdf (kyoto-u.ac.jp)
それと、去年ぐらいに単純に自分の興味から読んでいたこちらの本もわかりやすい上に、結び目理論のかなり高度なところまで導いてくれます。
結び目の不変量 (共立講座 数学の輝き 4) | 大槻 知忠, 新井 仁之, 小林 俊行, 斎藤 毅, 吉田 朋広 |本 | 通販 | Amazon
~編集後記~
前にもちょっと書いたけど(エネルギーとエントロピーを司る神々のゲーム【論文紹介】#9|喜多見奈美 (note.com))、こういう、論理の構造の美しさを愛でる感覚って、音楽の構造の美しさを愛でる感覚と奥深くで似ていると思う。結び目理論は、今までやってきたどんな数学とも似ていない斬新な構造だけど、すごく整合性が取れていて美しいと感じる。この記事の主要な部分をガーっと一気に書き終わった後、脳内でしばらく流れていた音楽はこれだった。
最後まで読んでいただきありがとうございます。気に入っていただけたら「スキ」ボタンを押したりフォローしたりしていただけますと私のモチベが上がります。内容についての質問や感想もお待ちしております。
また、研究機関には所属せずにやっておりますので、有料ジャーナルのアクセス料程度のサポートをいただけるとありがたいですし、今後の記事の質が上がるかもしれません。どうぞよろしくお願いいたします。
この記事が気に入ったらサポートをしてみませんか?
