正解のない社会での合意形成のダイナミクス【論文紹介】#20
哲学者のゴットハルト・ギュンターは、主観しか持ちえない我々がどのように思考を精緻化するかを考え、ヘーゲルの弁証法に対する批判として複弁証(polycontexturality)を提唱した。(これまた定まった訳語がないようなので、ここでは複弁証と訳す)
まず、ヘーゲルの弁証法は簡単に言うと、テーゼ(ある命題)とそれを否定するアンチテーゼを考え、その2項対立ではなく2つを包括するジンテーゼに至るという思考法である。ジンテーゼという一段高い思考に至る過程のことをアウフヘーベン(止揚)と言う。
これに対してギュンターは、1人の内省だけでそのような高度な思考をせずとも、2人のコミュニケーションによって弁証法を行えることがあると指摘した。具体的には次のとおりである。

図の文字色は、個人が持つ意見(政治的、宗教的思想ととらえてもよい)の色を示す。重要なのは、色を客観的にそのまま見ることは誰もできず、必ず主観という色眼鏡を通して見るということ。なので同じ対象を見てもそのあと染まる意見の色は人によって違うことがある。
まずC1で、左にある茶色の対象(命題)に対し、主体S1はそれを主観的に(色眼鏡を通して)観察した結果、青の意見に染まる。
次のC2で、主体S2は、左の対象を観察した後の主体S1を、自身の色眼鏡を通して観察した結果、緑の意見に染まる。
C3で、今度は主体S2が左の対象を直接、自身の色眼鏡を通して観察すると、さっきのS1を見たときとは違う色に見える。
いわば、主体S2にとっては「対象についてS1から聞いてたのと違うな」という不和が起こり、青の意見or緑の意見という2項対立ではなく、どちらか(もしかしたらどちらも)が色眼鏡をかけているなというジンテーゼ(一段高い思考)に至ることができる。これが2人のコミュニケーションによる複弁証の最も単純な事例である。
今回紹介する論文はこちら
共通の価値観なしに合意を得ようとするネットワークにおける集団的パターンと安定的誤解
Collective patterns and stable misunderstandings in networks striving for consensus without a common value system
(この論文紹介シリーズの前々回で、ウィトゲンシュタインの言語ゲームを実験的に精度よく検証したと言える論文を紹介したが(「これはスモウ」「スモウってこれか」言語集団におけるラベル付けの発生【論文紹介】#18|喜多見奈美 (note.com))、今回も、哲学の主張を実験的に検証するという似た事例と言える。)
本論文の複弁証ネットワークモデル(polycontext network model)は、ギュンターの複弁証を参考にした(Our model is motivated by Gotthard Günther’s polycontextural logic)と明記されている。
複弁証が大人数でやり取りされるときの統計的振る舞いを調べるために、エージェントベースモデルでシミュレーションしやすいよう、人の主観的判断基準と意見を次のようにモデル化する。
人の意見は色と考え、主観的判断基準は色眼鏡であり、隣人の意見を観察すると実際とは違う色に見えることがあるとし、客観的に(本来の色から)色がどう変わっているかはわからない(色眼鏡を外すことはできない)とする。そして、隣人を観測したらすぐにその色(色眼鏡を通して見た色)に染まるとする。日常的な経験からすると、このモデルにおいて、意見が即座に変更されることは奇妙に思えるかもしれない。しかし、このモデルが反映しているのは、意見の変化と世界観の変化の時間スケールの違いである。いわば、世間の風潮が変わるよりもずっと早く、個人の意見は変わったりする。

上が影響を受ける前(両者とも緑)、下が後
Aさんの主観では「Bさんが青なんだから私も青になろう」と考えてこうなっている。
図1は、緑の意見を持っているBさんを、Aさんが自分の色眼鏡を通して見たときの反応である。Aさんの色眼鏡(色変換規則)を通してBさんを見ると、AさんにとってはBさんは青の意見に見え、それに影響されてAさんは青の意見に染まる。
重要なので何度も言うが、主観的には必ず色眼鏡を通して見ている。Aさんにとっては「Bさんは青」としか見えていない。自分が色眼鏡をかけていることも認識していない。
意見の種類がC種類あるとすると、n番目のエージェントの意見はC次元ベクトルのうち1成分だけのベクトル$${c_n}$$であり、色眼鏡はC×Cの置換行列$${T_n}$$で表すことができる。n番目のエージェントがm番目のエージェントを主観的に観測する色は、$${c_m}$$ではなく、$${T_n}$$という色眼鏡を通した$${T_nc_m}$$である。例えば上図で、3つの意見、緑・赤・青をベクトルの1, 2, 3番目の成分とすると、「Aさんが緑のBさんを観測すると青に見える」のは次のように表記できる。
$${T_Ac_B}$$
$${=\begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{pmatrix}\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}=\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}}$$
通常このようなエージェントベースモデルでは、客観的な値とエージェントが主観的に観測する値は同じだが、本論文では、主観的な観測は必ず色眼鏡を通すとしたのが他には見られない興味深いところだ。
この複弁証ネットワークモデルでは、エージェント同士の反応を進めていくと、意見の変化が起こらなくなる互換的(compatible)なパターンが発生することがある。
互換性の簡単な例として2人で、意見(色)は2種類だけの例を考える。

例1)Aさんは色をそのまま認識し、Bさんは色を反転させて認識する(青から赤、赤から青の)色眼鏡をかけているとする。両者とも、相手と色が違えばすぐに相手に合わせるように色を変えるとする。
(1)まずAさんBさんともに赤で、BさんがAさんを観察すると、Bさんは「Aさんは青だな」と見て青になる。
(2)その後、AさんがBさんを観察すると、Aさんは「Bさんは青だな」と見て青になる。
(3)その後、BさんがAさんを観察すると、Bさんは「Aさんは赤だな」と見て赤になる。
(4)その後、AさんがBさんを観察すると、Aさんは「Bさんは赤だな」と見て赤になって、プロセスは(1)に戻ってループに入る。これは色がずっと変わり続け、互換的でない例である。
これは主観的に見ると、両者ともに同じように「あいつコロコロ意見変えてる」と観測される。どちらが色を変える色眼鏡をかけているかは両者とも主観的には気付かない。ただし、この不和から、どちらかは色を変える色眼鏡をかけているということには気付く。

例2)AさんBさんともに、色を反転させて認識する(青から赤、赤から青の)色眼鏡をかけているとする。
(1)まずAさんBさんともに赤で、BさんがAさんを観察すると、Bさんは「Aさんは青だな」と見て青になる。
(2)その後、AさんがBさんを観察すると、Aさんは「Bさんは赤だな」と見て色は変わらない。
(3)その後、BさんがAさんを観察すると、Bさんは「Aさんは赤だな」と見て色は変わらない。(2)に戻ってまたAさんが観測しても色は変わらず、(2)と(3)のループに入る。
これは、AさんとBさんは違う意見であるが、両者とも主観的には「相手は同じ意見だ」と思っていて意見はずっと変わらない。これは安定的誤解(stable misunderstanding)と呼ばれ、これは色変化が起こらないので互換的である。
安定的誤解は、他のエージェントベースモデルでは見られず、必ず主観を通して見るという設定のおかげで発生する興味深い現象である。
また、例0として、図を書くまでもないが、両者とも色を変えない色眼鏡で、同じ意見で落ち着く場合も、互換的なパターンである。
上記の例は、色変換を置換行列で考えるとわかりやすい。(この段落では、1番目の成分を赤、2番目の成分を青とする。)
例1で、Bさんの色眼鏡で赤のAさんを観測すると、
$${T_Bc_A}$$
$${=\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}\begin{pmatrix} 1 \\ 0 \end{pmatrix}=\begin{pmatrix} 0 \\ 1 \end{pmatrix}}$$と、青に見える。
その次に、Aさんの色眼鏡で青のBさんを観測すると、
$${T_Ac_B}$$
$${=\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}\begin{pmatrix} 0 \\ 1 \end{pmatrix}=\begin{pmatrix} 0 \\ 1 \end{pmatrix}}$$と、青に見える。
ここで、Bさんの色$${c_B}$$は、先ほどの$${T_Bc_A}$$の結果なので、これを代入すると、
$${T_AT_Bc_A}$$
$${=\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}\begin{pmatrix} 0 & 1 \\1 & 0 \end{pmatrix}\begin{pmatrix} 0 \\ 1 \end{pmatrix}}$$
$${=\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}\begin{pmatrix} 1 \\ 0 \end{pmatrix}=\begin{pmatrix} 0 \\ 1 \end{pmatrix}}$$
つまり、反応を1往復することは、相手と自分の2つの色眼鏡を重ねて$${T_AT_B}$$を通して自分自身$${c_A}$$を見ることとも解釈できる。それが元の自分と同じで色が変わらないなら互換的であり、違う色が見えるなら色が変わり互換的でない。例1では2つの色眼鏡を重ねた行列は$${T_AT_B=\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}}$$と色を反転させるので互換的でない。
この考え方を踏まえて例2を置換行列で表すと、
$${T_AT_Bc_A}$$
$${=\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}\begin{pmatrix} 0 & 1 \\1 & 0 \end{pmatrix}\begin{pmatrix} 0 \\ 1 \end{pmatrix}}$$
$${=\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}\begin{pmatrix} 1 \\ 0 \end{pmatrix}=\begin{pmatrix} 0 \\ 1 \end{pmatrix}}$$
2つの色眼鏡を重ねた行列は$${T_AT_B=\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}}$$と色を反転させないので互換的である。
また、例0も自明だが、2つの色眼鏡を重ねた行列は色を反転させないので互換的である。
一般に、i番目とj番目の2人のエージェントの場合、
$${T_i×T_j=I}$$($${I}$$は単位行列)
が成り立てば、互換的であるということである。これは色の数が3以上の場合でも、色眼鏡を2つ重ねたら色変化がなくなると考えれば同様である。
次に、人数が3以上のネットワーク中における互換性を、行列を用いて考えると次のようになる。

まず三角形の場合。
三角形全体で互換的であるためには、まず1つ目の条件として、AさんとBさん、BさんとCさん、CさんとAさんの3組とも互換的である必要があり、次のように表される。
$${T_A×T_B=I}$$, $${T_B×T_C=I}$$, $${T_C×T_A=I}$$
上記3式が同時に成り立つには、
$${T_A=T_B=T_C=T_A^{-1}}$$
でなければならない。この条件は、$${T_A,T_B,T_C}$$とも、単位行列と、すべての2色置換の行列が当てはまる。これが1つ目の条件。
もう一つの条件は、AさんがBさんに観察され、BさんがCさんに観察され、CさんがAさんに観察され、1周した結果(3つの色眼鏡を通して)も同じ色に見える必要があり、次のように表される。
$${T_AT_BT_C=I}$$
この条件は、$${T_A,T_B,T_C}$$とも、単位行列とすべての循環置換の行列が当てはまる。
しかし、1つ目の条件$${T_A=T_B=T_C}$$を考えると、
$${T_AT_BT_C=T_A^3=T_B^3=T_C^3=I}$$
となり、これを満たすのは$${T_A,T_B,T_C}$$とも、単位行列しかない。つまり、三角形のネットワークが互換的になるのは、全員が色を変えない色眼鏡の場合のみである。
次に、四角形の場合。
四角形全体で互換的であるためには、まず1つ目の条件として、AさんとBさん、AさんとCさんが互換的である必要があり、
$${T_A×T_B=I}$$, $${T_A×T_C=I}$$
BさんとCさんは直接つながっておらず、Dさんを介してのみつながっているので、
$${T_D×T_B=I}$$, $${T_D×T_C=I}$$
上記4式より、
$${T_A=T_D=T_B^{-1}}$$, $${T_B=T_C=T_A^{-1}}$$
まずこれが、各つながりが互換的である条件である。
次に、1周して同じ色に見える条件は、
$${T_BT_DT_CT_A=I}$$ これに上記の条件を使うと、
$${T_BT_DT_CT_A=T_BT_AT_BT_A=T_BT_B^{-1}T_BT_B^{-1}=I}$$
$${T_BT_DT_CT_A=T_CT_DT_CT_D=T_CT_C^{-1}T_CT_C^{-1}=I}$$
この条件を満たすのは、単位行列だけでなく、2色置換の行列が交互になる場合もありうる。つまり、色が交互に異なるがその状態で変わらない安定的誤解が生じる。
同様に5人以上を考えると、1周のループが偶数人ならきれいに交互になる安定的誤解になりうるが、奇数人なら交互に色を付けていってもどこかで不和が起こって安定的誤解にはなりえない。
ネットワーク全体が互換的な場合、そのネットワークは解決済み(solved)と呼ぶ。解決済みのネットワークはそれ以降、全体が互換的なので色の変化は起こらなくなる。そして重要なことは、互換性と解決済みは、エージェントの色には関係なく、色眼鏡の配置のみによって決まる。
さて複弁証ネットワークモデルの最後の要点であるが、関係認識論と世界観の哲学によれば、世界観は生きた経験によって形成され、それに応じて変化し、世界をどのように理解し、それにどのように対応するかを決定する。
複弁証ネットワークモデルとしては、周囲とのやり取りによって、色眼鏡の色が変わることもあり、それは次のようなルールで変更される(この部分こそがこのモデルの核心である)。
各エージェントは#Onと#Knの2つの内部カウンターを持ち、更新ステップは次のように進む:
全体でN人のネットワーク中から、n番目のエージェントAnがランダムに選択され、その隣人Amが1人選択される。
エージェントAnはAmの意見を主観的に観察する。
AnがAmを主観的に観察し、同じ意見に見える場合、Anの意見は変わらず、Anの内部カウンタ#Onだけが1だけ増加する。
異なる意見に見える場合、Anは自身の意見をその意見に変更し、内部カウンタ#Onと#Knの両方が1だけ増加する。
#Kn/#Onで表される、Anがその意見を変更した回数の割合があるパラメー タqを超えた場合、エージェントは利用可能なC!種類の色眼鏡から新しい色眼鏡をランダムに選択し、両方のカウンタをゼロにリセットする。Onは最終ステップの前に常に少なくとも1回増加されるので、分数#Kn/#Onは常に定義されていることに注意。
つまり、#Onは、その色眼鏡を通して見たトータルの人の数、#Knは、そのうち自分の意見が変わった回数。#Kn/#Onはその色眼鏡を通して自分の意見を変えた人の割合で、それがqを超えると、その色眼鏡は意見の変更を迫る頻度が高すぎて使いづらいので、ランダムに別の色眼鏡に変えるということである。
パラメータqには特に名前はついていないが、色眼鏡変更閾値とここでは呼びたい。
現実には#Kn, #Onは、正確に数えなくとも、感覚的に「なんか意見合わない人が多いなあ」と感じることによってこの変化は起こると思われる。これは菌類に見られるクオラムセンシングにも似ているが、この複弁証ネットワークモデルの場合、同じ状況でも色眼鏡の違いによって個人ごとに反応の仕方も違ってくるので「主観的クオラムセンシング」と言える。
さて、この複弁証ネットワークモデルの考え方にも慣れてきたところで、(私は慣れるのに時間がかかって、またしても記事の更新が遅くなってしまった)これを大量のエージェントでシミュレーションし、その統計的振る舞いを見てみる。
エージェントはランダム4次正則グラフとランダム3次正則グラフ、そして住宅街に住む人のような2次元の三角格子と正方格子状の配置という4パターンで行った。正方格子なら4近傍、三角格子なら6近傍とだけつながるとする。

ランダム3次正則グラフは、同様にノードから出る辺の数が3本のグラフ。
結果
まず、色眼鏡変更閾値qの値による振る舞いの違いを時間発展で見てみる。図3は、ランダム4次正則グラフでエージェント数200での結果である。

色眼鏡変更閾値qの値によって振る舞いが大きく異なっている。
qが小さすぎると(左)、全員色眼鏡が頻繁に変わって、色も頻繁に変わり、クラスタは成長しない。
qが大きすぎると(右)、色は変わっても色眼鏡は全然変わらず、これもクラスタは成長しない。
qが何らかのちょうどいい値のとき(中)のみ、同じ意見のクラスタがうまく成長する。
qがちょうどいいところで何が起こっているのか、前後を細かく刻んでプロットしてみたのが次の図。

最大クラスタの全人口に対する割合(上)と、各色眼鏡(無色、2色置換、循環)の普及率
どちらも横軸はqパラメータ
図5のグラフでは、ある臨界q値で突然、相転移のようにクラスタが急成長するという興味深い振る舞いが見られる。その臨界q値が、3次では0.5という"ちょうど"のような値になるのも、4次では0.43のような"絶妙"な値になるのも(何故その値になるのか理由はわからないが)興味深い。
また下のグラフは、各色眼鏡の種類の普及率を示している。3色の色変換の置換行列は3!=6種類のみで以下の通りである。これらはどのようにいくつ重ねても、6種類の内のいずれかになる(これは正三角形の対称群にも等しい)。
$${T_A=\begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}}$$, 無色
$${T_B=\begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{pmatrix}}$$, $${T_C=\begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{pmatrix}}$$, $${T_D=\begin{pmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \end{pmatrix}}$$, 2色置換
$${T_E=\begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{pmatrix}}$$, $${T_F=\begin{pmatrix} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{pmatrix}}$$, 循環
図5下のグラフの線の上下の薄い色は、100回シミュレーションして1σの(7割はこの範囲に収まる)ばらつきの範囲を示している。クラスタが急成長するq値では無色の色眼鏡が圧倒的になるが、それより少し高めのq値で2色置換もかなりの割合普及することもあるようだ。
この図5だけでもすでに、複弁証ネットワークにおいて合意形成が自然発生するのを見事に示しているが、次に示す格子模様も興味深い。

図6は、三角格子と正方格子でシミュレーションした結果で、色は意見ではなく色眼鏡の種類を示す。三角格子では、巨大な赤のクラスタに緑、青、紫の小さなクラスタが混ざっている。
正方格子では、左側に水色と黄色が交互の「安定的誤解」のクラスタができている(これを見たかった!)。互換性の解説時に示した通り、三角形のネットワークでは安定的誤解は起こらないが、四角形のネットワークでは起こりうる。無色の色眼鏡が圧倒的であるが、この安定的誤解の部分が、図5下のグラフの2色置換の色眼鏡の普及の主要因である。

a,bはクラスタサイズの平均、aは15程度、bは30程度で頭打ちになっているが、これをプロットした20000ステップ目ではまだクラスタが成長しきっていないと見て取れる。
c,dは図5と同様、上はクラスタサイズ、下は各色眼鏡の普及率(aとcは横軸の幅が違うことに注意) 興味深いのはdで、各色眼鏡の普及率が同程度になっているという点だ
三角格子と正方格子でq値ごとにクラスタサイズと各色眼鏡の普及率をプロットしたのが上図。
まず注目すべきはdの下、正方格子での各色眼鏡の普及率は、中心線はほぼ重なっていて、どれが普及するかはどれも確率としてはほぼ同じになっている。ばらつきの幅は、緑が小さめだが、青とオレンジはほぼ同じになっている。つまり、無色と同じくらいの確率で2色置換が同じくらい多く普及することもあるということだ。
またcの下、三角格子では安定的誤解が生じない影響か、図5のランダムグラフと比べてばらつきが小さくなっているのも興味深い。
クラスタ成長の幾何学的特徴を調べるために、クラスターの自己相似性とフラクタル次元を調べた。

(左)クラスタサイズ(横軸)とその数(縦軸)のプロット
サイズが小さいものは多く、大きいものは少ない。指数m=-2.3のきれいな指数法則に乗る。
(右)最大クラスターの縦または横の幅(横軸)とそのクラスターのメンバー数(縦)
この傾きはフラクタル次元df 三角格子ではdf=2に近く、正方格子ではdf=1.3程度
まず左のグラフはクラスタサイズとその数の両対数プロットであるが、これがきれいな指数法則に乗ることから、大小のクラスタ含むフィールド全体で、クラスタの分布は自己相似的であることがわかる。シミュレーションしているフィールドを拡大して見て、大きいクラスタを無視して(グラフの右下のほうを切り捨てて)も、切り捨てた後の最大のクラスタが一番右下となり、このグラフの形は変わらないので、拡大しても縮小してもフィールドの(統計的な)見え方は変わらない。つまり自己相似的である。
右のグラフは三角格子と正方格子における、最大クラスターの縦または横の幅とそのクラスターのメンバー数の両対数プロットで、この指数は、統計的には(←本論文ではこの点を割と慎重めに書いているが)フラクタル次元と解釈できる。やや雑な説明としては、指数が1(1次元)の場合は、クラスターの縦または横の幅Lに対してそこに含まれるメンバー数はLに比例、指数が2(2次元)の場合はLに対してそこに含まれるメンバー数はL^2に比例するからである。
三角格子では、表面張力のような効果が働いているようで、境界線はのっぺりしていて内部に異物も少なく2次元的に中身の詰まったクラスタとなっている。正方格子では木の枝か菌糸のように細長く繋がる隙間の多いクラスタになっていると想像できる。
最後に、色眼鏡変更閾値qによるクラスタの振る舞いの変化について概観する。
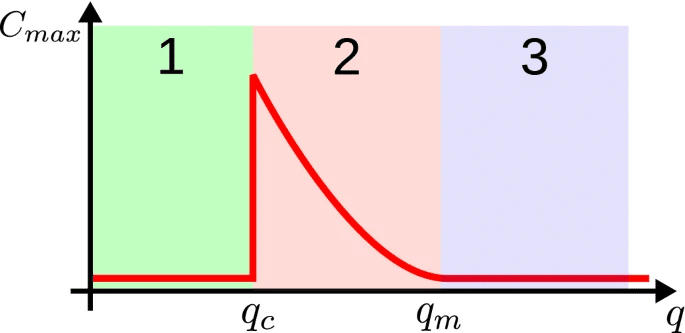
振る舞いの違いとして、上図のように3つの相に分けて解釈できる。
まずqが小さすぎると、色眼鏡が頻繁に変わってしまうために、クラスタはすぐ破壊されて成長しない。
qが大きすぎると、色眼鏡を全然変更しないために、意見が揃わずクラスタは成長しない(それでもゆっくりとは色眼鏡を変えるのでテールは右側に伸びている)。
qが小さすぎず大きすぎずちょうどいいところでクラスタは飛躍的に成長するようになる。
成長曲線の左側の臨界値で急激に立ち上がる理由としては、クラスタ破壊の効果が大きめであるために、最初の小さな核が発生する確率は小さいが、一度発生すれば急速に成長するためであると、観測から推察されている。
この段落は私の考察だが、色眼鏡変更閾値qは1つのパラメータでありながら、クラスタの成長速度と破壊頻度という2つの要素を同時に調整するパラメータと解釈できそうだ。まず、qはある程度小さくなければ色眼鏡の変更は起こらず、クラスタが成長することはない。qが小さければ”クラスタを成長させる効果”がまずある。それと同時に、qが小さすぎると色眼鏡が頻繁に変わってクラスタはすぐ破壊されて成長しない。つまり、qが小さければ”クラスタを破壊させる効果”も同時にある。問題は、両者がどれほど強いかのバランスである。思うに、本論文の設定では下図の左のように、成長の効果がある程度強いが破壊の効果は弱い、絶妙な窓の領域があるためにクラスタ成長が見られたと思われる。設定がちょっと違えば、下図の右のように、成長の効果よりも破壊の効果が強くてクラスタ成長が全然見られないこともあり得たと思われる。すごくシンプルな実験設定のようで、パラメータはqの1つしかないのに狭い窓がうまいこと開いてクラスタ成長が起こるのは、神の一撃のような絶妙な設計なのではないかと思われる。これが偶然かどれほどの試行錯誤の結果かは知らないが。
追加実験として、qのうち成長の効果と破壊の効果をうまく調整する方法、または2つの効果を別のパラメータに分けて調整する方法が何か考えられないかと思う。その要素がどこにあるか、ネットワークの構造かカウンタの設定か何かは不明だが。

成長の効果と保存の効果の合成によってクラスタ成長の上限が決まるイメージ
今後の研究の発展の可能性について、本論文でもかなり幅広く書かれている。
・ランダム正則グラフや格子状ネットワーク以外に、ERグラフやBAグラフのようなランダムなネットワークでは振る舞いはどう変わるか。
・ネットワークのつながりの次数に依存する閾値パラメータを導入し、次数の高いノードが自分の位置をより確信し、テーブルをより頻繁に変更するようにするのも面白いかもしれない。
・各ノードがq個の隣接ノードを観察し、その隣接ノードのうち所定の割合が間違った色を持つ場合にのみテーブルを変更するというq-voterモデルに匹敵するメカニズムに、モデルのダイナミクスを変換することも価値があるかもしれない。
・人々の行動をもう少し現実的にモデル化するために、エージェントのメモリーを減らすという興味深い修正も考えられる。これはより多くの揺らぎを生み出し、小さいが安定した少数クラスターの生成を避けることができる。
・さらに、可能な色の数Cを増やし、それによって異なる世界観の数C!を増やすことは興味深い。これは、より多様な誤解の可能性と、安定した部分的互換性のある世界観の可能性をもたらす。
複弁証ネットワークモデルはギュンターの哲学の実験的検証手法と言えるが、まだまだ奥深い複弁証の世界の窓をほんの少し覗いただけのようだ。
この記事が気に入ったらサポートをしてみませんか?
