CT検査（回折型断層撮影法）を数学的に表現する 　[1] ボルン近似

　レントゲン検査、CT検査、MRI検査など、今や病院では、人体の状態を知るための検査方法が数多く存在します。

　それは、装置や光源、それを制御する素子、コンピュータサイエンスによるアルゴリズムの発展など、様々な要因があるのですが。一方でその性質を知るための基本的な原理は（日本では）思ったより知られてなくて、どうやって使うかと言う実践的な内容が中心のような気がします。

　CT関係の研究者ならともかく、、、あまり理解が追いついていない数学的な話ってどうするの？と言うのを今回整理しておこうと思うわけです。

※今回は、数式については、文献[1]からのほぼ引用です。読めば大体わかるのですが、複雑な部分もあるかと思うので、いくつか混ぜ合わせて説明しようかなと思います

「光が散乱する現象」をどう表現する？

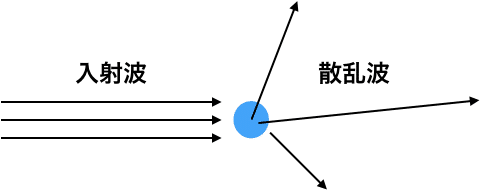
　青い部分で示した「まと」（誘電体）に入射波を当てて、そこから散乱される単色の光を考えましょう。通常、光はこのような条件の場合はあらゆる方向に散乱されますが、

・入射波と同じ方向の光→方向は同じ。強度は一番強い
・入射波に近い方向の散乱光→弱い
・入射波からある程度の角度を持った散乱光→弱い
・入射波と反対方向の散乱光→すごく弱い

と言う性質が予想されます。そうすると、光と言うのは、もっとざっくり書くと、こんな感じになると予想できますよね？

ここで、平面波、散乱波がわかれました。

０次波と１次波（脱線）

　あえてここで０次波、１次波といっていますが、（今回の散乱の問題では意味はありますが）光学においては色々な定義があるんですよね。

例えば、回折格子

※こちらが詳しい

http://racco.mikeneko.jp/Kougi/07a/IE/IE01pr.pdf

例えば、光学薄膜やガラスによる干渉

こんな感じで、光学の世界で「０次波」「１次波」が何を表しているかを文脈から読む必要があります。

入射波と散乱波

　今回は散乱の議論なので、一旦戻りまして、平面波と散乱波に分ける話に戻しましょう。

　この平面波と散乱波の特徴ですが、次のような特徴があります。

・平面波【０次波】は、例えば誘電体に色がついていたとすれば、それが吸収されて弱くなる。また厚みを持っていたとしたら、それに付随して減衰する。
・散乱波【１次波】は、誘電体内部の構造を反映する。誘電体が回折格子のように周期的な構造だったら一定の方向にのみ強い光が放射されるし、均質な球のような性質があったら球の中心から放射状に光が放射される。

　１次波はちょっとわかりにくいかもしれませんね。

　回折格子のような構造はなんとなく想像つくかと思いますが、均質な球ってなんだ？と思うかもしれません。これはシンプルに、球の中心に点電荷がいたら、クーロン力による電場が生じているのと同じイメージで理解していただければ大丈夫かと思います。

　平面波と散乱波の違い、イメージ浮かびましたでしょうか？

散乱波とCT

　散乱波は、物質の内部構造を表すものです。

　例えば、人体を対象に扱った場合は、具体的な筋肉や骨格などの構造を持っているので、散乱波の特性が重要視されます。平面波でわかることは限られていて、例えば構造全体の大きさはある程度わかると思いますが、構造そのものを理解できません。

　散乱波の特性を理解することこそ、その物質の本質を知ることができるのです。（大事なことなので２度言いました）

散乱波を数式で表現する

　そんな散乱波ですが、平面波と比べると、実際にどんな特性を持っているのかをイメージしにくいかもしれません。

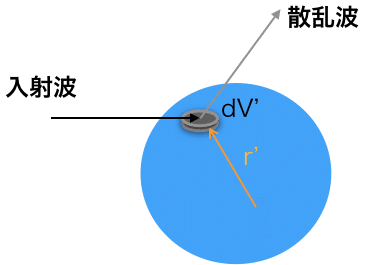
入射波は誘電体のどこかにあたり、回折したり反射・屈折したりします。また、１次波は構造を表しているので、誘電体の内部でも、何がしか散乱波の特性を表すような散乱があれば、その方向も散乱波に混ざって放射されるでしょう。

　そこで、その誘電体球の微小体積をdV'、誘電体球の基準点からの位置ベクトルをr'とします。そして、dV'を基準に放射される電場をU(r')とおきます。

　そうすると、この体積分dV'が散乱させる電場は、Fと言う何かの特定の値分だけUを減らすようになります。そこで、このFも位置ベクトルr'に依存しているものとすると、

が散乱されるでしょう。

電場はどう散乱される？

　散乱されるのはいいのですが、これだけではどの点に向かって散乱されるのかがわかりません。

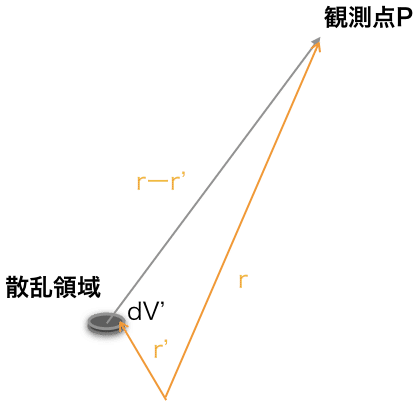
　今、観測点Pに、dV'から散乱されたものとすると、両者間の位置ベクトルはr-r'となります。この領域が散乱を起こし、観測点Pに放射されるわけです。

　ところで思い出して欲しいのですが、外部電荷や外部電流が存在しない場合、波動方程式が一般の電場Eに対して成立します。

光の振動数ωは時間に対して相当早く（≒fsオーダ）、CTの系ではこの特徴を捉えることはできないので、このEはexp(-iωt)に比例しているものとしましょう。微分方程式は、

分散関係ω=ck, 屈折率の関係v=c/nより、ω/v=k×nとなり、

さらに、球座標で変換します。散乱された周辺に対しては、場が等方的に散乱されるためです。そうすると、ラプラシアンは書き換えることができて、|r-r'|を使って

以上から、E(r'')r''をfとしてまとめます。

さらに、fは平面波の波動方程式の解と一致しますので、f(r'')は三角関数の形になります。その表現をオイラーの方程式の表現で書きます。ただし、進行方向として+r"と-r"の両方があるのですが、-r"の解は散乱を表していないので無視すると、

したがって、球面波は三角関数に比例し、距離に反比例します。この特性を、dV'の式にかけることで、位置rに至る電場を求めることができます。つまり、

ポテンシャル散乱の積分方程式

これを積分して、電場Usを計算できます。

　上記の方程式をポテンシャル散乱の積分方程式と言います。しかし、通常、ここのU(r')を計算するのは非常に大変なので、近似をします。

ボルン近似

　さてU(r')なのですが、これは全体空間の波です。ここで、波の強度の強さの話を思い出しましょう。

・入射波と同じ方向の光→方向は同じ。強度は一番強い
・入射波に近い方向の散乱光→弱い
・入射波からある程度の角度を持った散乱光→弱い
・入射波と反対方向の散乱光→すごく弱い

というわけなので、入射波と同じ方向の光以外は言うほど強くないわけです。したがって、ざっくりとU(r')は方向ベクトルs0に進む平面波くらいしかないぜ！として近似して

としてしまいます。これをボルン近似と言います。いま、誘電体の領域を積分領域として、積分方程式に突っ込むと、

これが、rの遠方で計算すれば、散乱波はr=rsとして、

したがって、散乱によって、どれだけ振幅が減少するかを表す関数F(r')のフーリエ変換に比例して、球面波が表現されます。この特性により、F(r')の情報が保存されるのです。このF(r')を散乱因子といい、誘電体とした物質の内部構造を知るための固有情報となります。

後半へ続く

　散乱因子と散乱された場がフーリエ変換の関係性になり、それは構造の情報握っていると分かりました。後半では、実際にCTの光学系を想定して、CTにおける(x,y)のフーリエ変換の関係性、入射波と散乱波の波数の関係性を示します。

補足

　この過程、実は厳密性という意味ではちょっと足りていなくて、定性的な説明で持ってきています。ディラックのδ関数やグリーンの定理を使った証明は[1]に書いてますので、興味がある方はご覧ください。

　ここまで、全て電磁気学の議論でボルン近似の議論をしてきましたが、電場Uを波動関数、散乱因子Fをポテンシャル場とすると、量子力学の世界でも同じような近似が成立します。

参考文献

[1] M.Born, E.Wolf., "Principles Of Optics" (2006)　：　名著です！