
ジオメトリシェーダーでVket5-DCのNodeRingをつくる
先日、バーチャルマーケット5の会場「Default Cube」のUI/UXデザインについての記事を公開しましたが、その中で紹介したNodeRingの制作過程を紹介します。本記事ではDefault Cube(以下DC)の説明は端折ります。
はじめてUnityのジオメトリシェーダーにトライしました。作っていてとてもおもしろかったので、なにかの参考になればと思います。
ジオメトリシェーダーの詳しい解説ではなく、どんなことをしたら何ができるかという概説なので、ちゃんと勉強したい場合は他の方が書いているより良い記事をググっていただければと思います。
つくりたいもの
Default Cubeは出展者ブースを召喚する仕組み。
5グループ(5色)×各4ブース=計20ブースについて、どのグループのブースをいくつ召喚したか視覚的に把握するためのマップがほしかった。そこでこういうものをつくろうと考えた。

1. ブース召喚 → 対応するNodeが点灯
2. 隣り合うNodeが点灯 → Linkが点灯
3. 全体としてのRingが回転しつつ、Nodeがランダムにゆらぐ
つくりたいもののイメージはできたけど、いくつか懸念があった。
1. 会場によってブース数が20とは限らない
2. ブース数の確定はVket開会のわりと直前
機能とルックに加えて、会場によるブース数の差を簡単に制御したい。
パーツごとにモデルやマテリアルやアニメーションをつくるのはそもそも非効率だし、会場ごとの差分や急な変更に対応できない。
何で作るか? → 1つのシェーダーで書き切ろう!
ジオメトリシェーダー
ジオメトリシェーダーとは、超簡単に言うと…
入力したメッシュの頂点データをもとに、頂点数を増減させたり頂点位置を変えたり、その頂点をもとに新たにメッシュを生成したりできるシェーダーです。
(正直「は?なんでもありかよ…」と思いました)
今回は、以下の図のように、たった1つの三角ポリゴンからNodeとなる立方体やLinkとなる四角柱のひとまとまりを生成します。こんな悪魔的なことをしていいのか、ちょっと罪悪感を感じます。

5グループ同じものをつくるので元となるメッシュは5ポリゴン
というわけで、以下に実際にできあがったシェーダーの中身の解説をしていきます。(コード全文は記事の一番下に記載しているので、全体像を知りたい方は先にそちらをご参照ください。)
Properties
最初にProperties内に必要なパラメーターをすべて書いていきます。
今回一番大事なブースの状態には「存在しない/未召喚/召喚済み」の3つの状態があります。これを「0/1/2」に置き換えてマテリアルのプロパティからいつでも変えられるように_BoothXXという変数にします。その他はだいたいルック調整やゆらぎの調整のための変数です。
Properties
{
_MainTex ("MainTex", 2D) = "white" {}
[HDR] _Color ("Color", Color) = (1,1,1,1)
_Speed ("Floating Speed", Float) = 0.2
_RotationSpeed ("Rotation Speed", Float) = 0.4
_CubeScale ("Cube Scale", Float) = 0.006
_RingScale ("Ring Scale", Float) = 0.25
_Thickness ("LineThickness", Range(0, 1.0)) = 0.5
_RFuwa ("R Fuwa Rate", Range(0, 1.0)) = 0.2
_YFuwa ("Y Fuwa Rate", Range(0, 1.0)) = 0.025
_BoothR1 ("Booth_R1", Float) = 1
_BoothR2 ("Booth_R2", Float) = 1
_BoothR3 ("Booth_R3", Float) = 1
_BoothR4 ("Booth_R4", Float) = 1
_BoothM1 ("Booth_M1", Float) = 1
_BoothM2 ("Booth_M2", Float) = 1
_BoothM3 ("Booth_M3", Float) = 1
_BoothM4 ("Booth_M4", Float) = 1
_BoothY1 ("Booth_Y1", Float) = 1
_BoothY2 ("Booth_Y2", Float) = 1
_BoothY3 ("Booth_Y3", Float) = 1
_BoothY4 ("Booth_Y4", Float) = 1
_BoothG1 ("Booth_G1", Float) = 1
_BoothG2 ("Booth_G2", Float) = 1
_BoothG3 ("Booth_G3", Float) = 1
_BoothG4 ("Booth_G4", Float) = 1
_BoothC1 ("Booth_C1", Float) = 1
_BoothC2 ("Booth_C2", Float) = 1
_BoothC3 ("Booth_C3", Float) = 1
_BoothC4 ("Booth_C4", Float) = 1
}マテリアル画面でみるとこうなります ↓↓
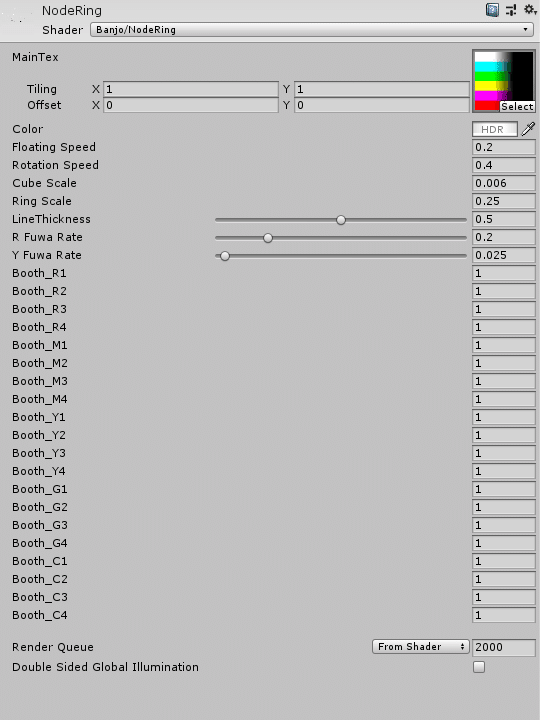
SubShader内
つづいて、シェーダーの中身を書いていきます。ジオメトリシェーダーを用いるのでPass内で「#pragma geometry geom」と宣言しています。位置は頂点シェーダーとフラグメントシェーダーの間です。
SubShader
{
Tags { "RenderType"="Opaque" "Queue"="Geometry" }
LOD 100
Pass
{
CGPROGRAM
#pragma vertex vert
#pragma geometry geom
#pragma fragment frag
#include "UnityCG.cginc"
#define PI 3.1415926535
//ここに書いていく
ENDCG
}
}便利グッズ-1
ここから先は上記の「//ここに書いていく」の中身になります。
最初に便利グッズとして、立方体の頂点座標cubeVtxと四角形の頂点座標sqVtxをつくっておきます。のちのち立方体や四角形を生成したいときに、ここに格納された頂点を呼び出して使います。
ちなみにcubeVtxが24個あるのは、四角形を6面生成しているためです。
// 立方体の頂点座標
static const float3 cubeVtx[24] = {
float3(0.5, -0.5, 0.5), float3(0.5, 0.5, 0.5), float3(-0.5, -0.5, 0.5),
float3(-0.5, 0.5, 0.5), float3(-0.5, -0.5, -0.5), float3(-0.5, 0.5, -0.5),
float3(0.5, -0.5, -0.5), float3(0.5, 0.5, -0.5), float3(-0.5, 0.5, -0.5),
float3(-0.5, 0.5, 0.5), float3(0.5, 0.5, -0.5), float3(0.5, 0.5, 0.5),
float3(0.5, -0.5, -0.5), float3(0.5, -0.5, 0.5), float3(-0.5, -0.5, -0.5),
float3(-0.5, -0.5, 0.5), float3(0.5, -0.5, -0.5), float3(0.5, 0.5, -0.5),
float3(0.5, -0.5, 0.5), float3(0.5, 0.5, 0.5), float3(-0.5, -0.5, 0.5),
float3(-0.5, 0.5, 0.5), float3(-0.5, -0.5, -0.5), float3(-0.5, 0.5, -0.5)
};
// 四角形の頂点座標
static const float3 sqVtx2[4] = {
float3(0.001, 0, 0.001), float3(0.001, 0, -0.001),
float3(-0.001, 0, -0.001), float3(-0.001, 0, 0.001)
};構造体
続いて、シェーダーに渡す引数を格納した構造体を用意します。
・「頂点シェーダー」→「ジオメトリシェーダー」はv2g
・「ジオメトリシェーダー」→「フラグメントシェーダー」はg2f
どちらも頂点の位置(POSITION)とUV座標(TEXCOORD0)だけ使います。のちに解説しますが、余計なものを含めずスリムにしておきます。
struct appdata
{
float4 vertex : POSITION;
float2 uv : TEXCOORD0;
};
struct v2g
{
float4 vertex : POSITION;
float2 uv : TEXCOORD0;
};
struct g2f
{
float4 vertex : SV_POSITION;
float2 uv : TEXCOORD0;
};パラメーターの取り込み
次に、Propertiesに書いたパラメーターの値をシェーダー内で変数として受け取れるようにします。ここではさらに、長ったるい20個のブース状態の変数をBooth[20]に格納しました。
sampler2D _MainTex;
float4 _Color;
float _Speed;
float _RotationSpeed;
float _CubeScale;
float _RingScale;
float _Thickness;
float _RFuwa;
float _YFuwa;
float _BoothR1;
float _BoothR2;
float _BoothR3;
float _BoothR4;
float _BoothM1;
float _BoothM2;
float _BoothM3;
float _BoothM4;
float _BoothY1;
float _BoothY2;
float _BoothY3;
float _BoothY4;
float _BoothG1;
float _BoothG2;
float _BoothG3;
float _BoothG4;
float _BoothC1;
float _BoothC2;
float _BoothC3;
float _BoothC4;
// ブースの状態を格納 0=なし/1=未展開/2=展開済み
static float Booth[20] = {
_BoothR1, _BoothR2, _BoothR3, _BoothR4,
_BoothM1, _BoothM2, _BoothM3, _BoothM4,
_BoothY1, _BoothY2, _BoothY3, _BoothY4,
_BoothG1, _BoothG2, _BoothG3, _BoothG4,
_BoothC1, _BoothC2, _BoothC3, _BoothC4,
};便利グッズ-2
そして、さらに便利グッズとして2つの関数を導入しておきます。
1つめのrandは0〜1の疑似的な乱数を返す有名な関数です。Nodeのゆらぎをつくるのに使います。
2つめのQuaternionToMatrixは「kumak1’s blog」さんの記事からお借りしました。回転軸ベクトルと回転角から回転行列を求める関数です。こちらは2つのNode間にLinkを生成するときに使います。
float rand(float2 co){
return frac(sin(dot(co.xy, float2(12.9898,78.233))) * 43758.5453);
}
float3x3 QuaternionToMatrix(float3 axis, float theta) {
float3 a = normalize(axis);
thita *= 3.14159265;
float s = sin(theta);
float c = cos(theta);
float r = 1.0 - c;
return float3x3(
a.x * a.x * r + c, a.y * a.x * r + a.z * s, a.z * a.x * r - a.y * s,
a.x * a.y * r - a.z * s, a.y * a.y * r + c, a.z * a.y * r + a.x * s,
a.x * a.z * r + a.y * s, a.y * a.z * r - a.x * s, a.z * a.z * r + c
);
};頂点シェーダー
ようやく準備が整い、各シェーダーを書いていく段階に来ました。最初の頂点シェーダーvertは、受け取った値を左から右へ受け流すだけです。
v2g vert (appdata v)
{
v2g o;
o.vertex = v.vertex;
o.uv = v.uv.xy;
return o;
}ジオメトリシェーダー-1 Nodeをつくる
さて、本題のジオメトリシェーダーgeomです。
まず[maxvertexcount(144)]で生成したい頂点数を宣言します。
この頂点数には制限があり、頂点数×1頂点の要素数を1024以下にする必要があります。今回は144頂点×(4要素(POSITION)+2要素(TEXCOORD0))=864です。構造体をスリムにする理由はこれですが、それでもけっこうリッチに使っているぽい。
void geom()の中は呪文みたいなものが並びますが、ここはジオメトリシェーダーの作法に従って、決められた書き方に沿って書くのみです。一点、ここで便利なのがuint gid : SV_PrimitiveIDです。今回は5ポリゴンのメッシュをぶちこむので、各ポリゴンのIDから0〜4の値を取り出せます。グループごとのIDということでgidと名付けました。
// geomで1polyから144頂点を生成
[maxvertexcount(144)]
void geom (triangle v2g IN[3], uint gid : SV_PrimitiveID, inout TriangleStream<g2f> stream) {
// 続く続いて、20個のNodeの座標を格納するppos[20]をつくります。初期値はすべて(0,0,0)ですが、このあと計算した座標をこちらに反映し、後にNode間にLinkを生成する際に、隣り合う2つのNode座標を参照するのに使います。
// 点座標の格納庫
float3 ppos[20] = {
float3(0,0,0), float3(0,0,0), float3(0,0,0), float3(0,0,0),
float3(0,0,0), float3(0,0,0), float3(0,0,0), float3(0,0,0),
float3(0,0,0), float3(0,0,0), float3(0,0,0), float3(0,0,0),
float3(0,0,0), float3(0,0,0), float3(0,0,0), float3(0,0,0),
float3(0,0,0), float3(0,0,0), float3(0,0,0), float3(0,0,0),
};そして、ここからNodeとLinkを一気につくっていきます。
1. 最初にNodeの座標を決めます。先程名付けたgidとfor文でNodeのIDとなるpid(0〜19の値)が作れるので、これで円周を20等分する点をつくります。
2. 次に、各点に半径方向のゆらぎ・Y軸方向のゆらぎ・NodeRing全体の回転を与えます。randで各点ごとのランダムな値を生成して、時間とともに三角関数のなかにつっこみます。この辺りのゆらぎのつくりかたはphi16さんのFuwaParticleに負うところが大きいです。
3. できた点をNodeの座標pposに格納しておきます。
// リング上に立方体を生成
[unroll]
for ( int v = 0; v < 4; v++ ) {
float pid = gid * 4 + v; // NodeのID
float angle = 2 * PI * 0.05 * pid; // 円周20等分に点を割り当て
float3 fpos = float3(cos(angle), 0, sin(angle)) * _RingScale;
float ra = rand(uv + pid); // 点ごとのランダムな値 0~1
float fr = t * (ra + 0.5);
fpos.xz *= cos(fr) * _RFuwa + 1; // 半径方向のゆらぎ
fpos.y += sin(fr * (ra + 2)) * _YFuwa * (step(0.5, ra) * 2 - 1); // y方向のゆらぎ
fpos.xz = mul(fpos.xz, float2x2(cos(t2),-sin(t2),sin(t2),cos(t2))); // 全体の回転
ppos[pid] += fpos; // 点座標を格納
// 続く
2つのゆらぎとNodeRing全体の回転の図
4. 各Nodeに生成する立方体の色は、その立方体が所属するグループ(5種)とブース状態(未召喚/召喚済み)の2要素、つまりgidとBooth[pid]で決まります。そこで、すべての色パターンを含む一枚のテクスチャを用意した上で、立方体の各頂点のuv座標cuvをgidとBooth[pid]で決めます。
// gidとブース状態で色を決定
float2 cuv = float2(0.62 - 0.4 * (Booth[pid] - 1), 0.166 * gid + 0.083);
色のパレットとなるテクスチャ
gidから縦(カラー)が、Booth[pid]から横(明度)が決まる
5. Node座標を中心とする立方体を生成します。for文を繰り返すことで、4頂点から四角形ポリゴンをつくる、を6回行って立方体にする、ということをします。この時、便利グッズ-1で準備した立方体の頂点座標cubeVtxを使います。また、ブースがない場合は立方体のスケールを0に、ブースが召喚済みなら立方体のスケールが変わるようにしています。
// fposの位置に立方体を生成
[unroll]
for ( int j = 0; j < 6; j++ ) {
[unroll]
for ( int k = 0; k < 4; k++ ) {
int idx = j * 4 + k;
float3 localP = cubeVtx[idx] * _CubeScale * Booth[pid];
localP += fpos.xyz;
o.vertex = float4(localP, 1.0);
o.vertex = UnityObjectToClipPos(o.vertex);
o.uv = cuv;
stream.Append(o);
}
stream.RestartStrip();
}
}ちなみに、stream.Append(o)は出力するメッシュの頂点を1点ずつリストに追加していっているイメージで、今回の場合は4点集まったら次のメッシュに進むようにstream.RestartStrip()でリストを更新します。この2つをfor文の中で正しい位置に書く必要があります。
以上でNodeの位置に立方体が生成できました。
ジオメトリシェーダー-2 Linkをつくる
6. 続いて、Node同士を結ぶLinkをつくります。Linkは表現上は線ですが、実際は「側面だけの四角柱」でつくります。
Linkをつくるためには、隣り合う2つのNode座標を調べる必要があります。先の工程でpposに各Node座標を格納しているので、ppos[n]とppos[n+1]が使えます。ここから、2つのNode間の単位ベクトルvec、ベクトル長さlec、y軸方向単位ベクトルとvecの回転軸axis、回転角thetaを求めておきます。
// 2つの点を繋ぐ線(四角柱)を生成
[unroll]
for ( int m = 0; m < 3; m++ ) {
float tid = gid * 4 + m;
// 隣り合う2点のベクトルと距離を算出 ベクトルに直行する平面の回転角を算出
float3 vec = normalize(ppos[tid+1] - ppos[tid]);
float len = length(ppos[tid+1] - ppos[tid]);
float3 axis = normalize(cross(vec, float3(0,1,0)));
float theta = acos(dot(vec, float3(0,1,0)));
// 続く
単位ベクトルvec、回転軸axis、回転角thetaの関係を示した図
7. 隣り合う2つのNodeが点灯しているときだけLinkが点灯するようにしたいので、Nodeの色を決定した際と同じ仕組みで、今度はgidとBooth[n+1]とBooth[n]で色が決定するようにします。
// 両端の状態で色を決定
float2 cuv = float2(0.65 - 0.1 * (Booth[tid] - 1) * (Booth[tid+1] - 1), 0.166 * gid + 0.083);
// 続く8. Linkとなる四角柱の側面をつくります。さきほど求めた回転軸axisと回転角thetaを、便利グッズ-2で用意したQuaternionToMatrixに放り込み、始点に生成した正方形を終点の方向に向けます。その正方形のうちの2点と、単位ベクトルvecとベクトル長さlecよって求めた終点側の対応する2点の合わせて4点から、側面が生成できます。なお、終点のNodeが存在しない場合はLinkも存在しないので、Booth状態が0の場合は長さが0になるようになっています。
あとはこれをfor文で4回繰り返してLinkも完成、ジオメトリシェーダーの役目はこれで終わりです。
[unroll]
for ( int n = 0; n < 4; n++ ) {
[unroll]
for ( int q = 0; q < 2; q++ ) {
//始点の2点を生成
float3 tpos = mul(QuaternionToMatrix(axis, theta), sqVtx[n + q] * _Thickness) + ppos[tid];
o.vertex = float4(tpos, 1.0);
o.vertex = UnityObjectToClipPos(o.vertex);
o.uv = cuv;
stream.Append(o);
//終点の2点を生成
float3 tpos2 = tpos + vec * len * step(0.5, Booth[tid+1]);
o.vertex = float4(tpos2, 1.0);
o.vertex = UnityObjectToClipPos(o.vertex);
o.uv = cuv;
stream.Append(o);
}
stream.RestartStrip();
}
}
}フラグメントシェーダー
最後にジオメトリシェーダーからフラグメントシェーダーfragにバトンタッチですが、すでにやることは終わっているので、特になにもしていません。
fixed4 frag (g2f i) : SV_Target
{
float4 col = tex2D (_MainTex, i.uv) * _Color;
return col;
}おわりに
以上、DefaultCubeのNodeRingの解説でした。(初トライなので変なところはあるかも…)
ジオメトリシェーダーを使えばかなり自由な表現が可能になるだけでなく、VR空間内のUIなど機能性を求められる場面でも、2DUIの常識にとらわれず、機能と表現をひとつの体験/ものとしてゼロから設計しなおすことができると思います。やったね。VRの醍醐味だね。(終わり)

・・・・・(以下、コード全文)・・・・・
Shader "Banjo/NodeRing"
{
Properties
{
_MainTex ("MainTex", 2D) = "white" {}
[HDR] _Color ("Color", Color) = (1,1,1,1)
_Speed ("Floating Speed", Float) = 0.2
_RotationSpeed ("Rotation Speed", Float) = 0.4
_CubeScale ("Cube Scale", Float) = 0.006
_RingScale ("Ring Scale", Float) = 0.25
_Thickness ("LineThickness", Range(0, 1.0)) = 0.5
_RFuwa ("R Fuwa Rate", Range(0, 1.0)) = 0.2
_YFuwa ("Y Fuwa Rate", Range(0, 1.0)) = 0.025
_BoothR1 ("Booth_R1", Float) = 1
_BoothR2 ("Booth_R2", Float) = 1
_BoothR3 ("Booth_R3", Float) = 1
_BoothR4 ("Booth_R4", Float) = 1
_BoothM1 ("Booth_M1", Float) = 1
_BoothM2 ("Booth_M2", Float) = 1
_BoothM3 ("Booth_M3", Float) = 1
_BoothM4 ("Booth_M4", Float) = 1
_BoothY1 ("Booth_Y1", Float) = 1
_BoothY2 ("Booth_Y2", Float) = 1
_BoothY3 ("Booth_Y3", Float) = 1
_BoothY4 ("Booth_Y4", Float) = 1
_BoothG1 ("Booth_G1", Float) = 1
_BoothG2 ("Booth_G2", Float) = 1
_BoothG3 ("Booth_G3", Float) = 1
_BoothG4 ("Booth_G4", Float) = 1
_BoothC1 ("Booth_C1", Float) = 1
_BoothC2 ("Booth_C2", Float) = 1
_BoothC3 ("Booth_C3", Float) = 1
_BoothC4 ("Booth_C4", Float) = 1
}
SubShader
{
Tags { "RenderType"="Opaque" "Queue"="Geometry" }
LOD 100
Pass
{
CGPROGRAM
#pragma vertex vert
#pragma geometry geom
#pragma fragment frag
#include "UnityCG.cginc"
#define PI 3.1415926535
// 立方体の頂点座標
static const float3 sqVtx[24] = {
float3(0.5, -0.5, 0.5), float3(0.5, 0.5, 0.5),
float3(-0.5, -0.5, 0.5), float3(-0.5, 0.5, 0.5),
float3(-0.5, -0.5, -0.5), float3(-0.5, 0.5, -0.5),
float3(0.5, -0.5, -0.5), float3(0.5, 0.5, -0.5),
float3(-0.5, 0.5, -0.5), float3(-0.5, 0.5, 0.5),
float3(0.5, 0.5, -0.5), float3(0.5, 0.5, 0.5),
float3(0.5, -0.5, -0.5), float3(0.5, -0.5, 0.5),
float3(-0.5, -0.5, -0.5), float3(-0.5, -0.5, 0.5),
float3(0.5, -0.5, -0.5), float3(0.5, 0.5, -0.5),
float3(0.5, -0.5, 0.5), float3(0.5, 0.5, 0.5),
float3(-0.5, -0.5, 0.5), float3(-0.5, 0.5, 0.5),
float3(-0.5, -0.5, -0.5), float3(-0.5, 0.5, -0.5)
};
// 四角形の頂点座標
static const float3 sqVtx2[4] = {
float3(0.001, 0, 0.001), float3(0.001, 0, -0.001),
float3(-0.001, 0, -0.001), float3(-0.001, 0, 0.001)
};
struct appdata
{
float4 vertex : POSITION;
float2 uv : TEXCOORD0;
};
struct v2g
{
float4 vertex : POSITION;
float2 uv : TEXCOORD0;
};
struct g2f
{
float4 vertex : SV_POSITION;
float2 uv : TEXCOORD0;
};
sampler2D _MainTex;
float4 _Color;
float _Speed;
float _RotationSpeed;
float _CubeScale;
float _RingScale;
float _Thickness;
float _RFuwa;
float _YFuwa;
float _BoothR1;
float _BoothR2;
float _BoothR3;
float _BoothR4;
float _BoothM1;
float _BoothM2;
float _BoothM3;
float _BoothM4;
float _BoothY1;
float _BoothY2;
float _BoothY3;
float _BoothY4;
float _BoothG1;
float _BoothG2;
float _BoothG3;
float _BoothG4;
float _BoothC1;
float _BoothC2;
float _BoothC3;
float _BoothC4;
// ブースの状態を格納 0=なし/1=未展開/2=展開済み
static float Booth[20] = {
_BoothR1, _BoothR2, _BoothR3, _BoothR4,
_BoothM1, _BoothM2, _BoothM3, _BoothM4,
_BoothY1, _BoothY2, _BoothY3, _BoothY4,
_BoothG1, _BoothG2, _BoothG3, _BoothG4,
_BoothC1, _BoothC2, _BoothC3, _BoothC4,
};
float rand(float2 co){
return frac(sin(dot(co.xy, float2(12.9898,78.233))) * 43758.5453);
}
float3x3 QuaternionToMatrix(float3 axis, float theta) {
float3 a = normalize(axis);
thita *= 3.14159265;
float s = sin(theta);
float c = cos(theta);
float r = 1.0 - c;
return float3x3(
a.x * a.x * r + c, a.y * a.x * r + a.z * s, a.z * a.x * r - a.y * s,
a.x * a.y * r - a.z * s, a.y * a.y * r + c, a.z * a.y * r + a.x * s,
a.x * a.z * r + a.y * s, a.y * a.z * r - a.x * s, a.z * a.z * r + c
);
};
v2g vert (appdata v)
{
v2g o;
o.vertex = v.vertex;
o.uv = v.uv.xy;
return o;
}
// geomで1polyから144頂点を生成
[maxvertexcount(144)]
void geom (triangle v2g IN[3], uint gid : SV_PrimitiveID, inout TriangleStream<g2f> stream) {
float2 uv = (IN[0].uv + IN[1].uv + IN[2].uv) / 3;
g2f o;
float t = _Time.y * _Speed;
float t2 = _Time.y * _RotationSpeed;
// 点座標の格納庫
float3 ppos[20] = {
float3(0,0,0), float3(0,0,0), float3(0,0,0), float3(0,0,0),
float3(0,0,0), float3(0,0,0), float3(0,0,0), float3(0,0,0),
float3(0,0,0), float3(0,0,0), float3(0,0,0), float3(0,0,0),
float3(0,0,0), float3(0,0,0), float3(0,0,0), float3(0,0,0),
float3(0,0,0), float3(0,0,0), float3(0,0,0), float3(0,0,0),
};
// リング上に立方体を生成
[unroll]
for ( int v = 0; v < 4; v++ ) {
float pid = gid * 4 + v; // 点のID
float angle = 2 * PI * 0.05 * pid; // 円周20等分に点を割り当て
float3 fpos = float3(cos(angle), 0, sin(angle)) * _RingScale;
float ra = rand(uv + pid); // 点ごとのランダムな値 0~1
float fr = t * (ra + 0.5);
fpos.xz *= cos(fr) * _RFuwa + 1; // 半径方向のゆらぎ
fpos.y += sin(fr * (ra + 2)) * _YFuwa * (step(0.5, ra) * 2 - 1); // y方向のゆらぎ
fpos.xz = mul(fpos.xz, float2x2(cos(t2),-sin(t2),sin(t2),cos(t2))); // 全体の回転
ppos[pid] += fpos; // 点座標を格納
// gidとブース状態で色を決定
float2 cuv = float2(0.62 - 0.4 * (Booth[pid] - 1), 0.166 * gid + 0.083);
// fposの位置に立方体を生成
[unroll]
for ( int j = 0; j < 6; j++ ) {
[unroll]
for ( int k = 0; k < 4; k++ ) {
int idx = j * 4 + k;
float3 localP = cubeVtx[idx] * _CubeScale * Booth[pid];
localP += fpos.xyz;
o.vertex = float4(localP, 1.0);
o.vertex = UnityObjectToClipPos(o.vertex);
o.uv = cuv;
stream.Append(o);
}
stream.RestartStrip();
}
}
// 2つの点を繋ぐ線(四角柱)を生成
[unroll]
for ( int m = 0; m < 3; m++ ) {
float tid = gid * 4 + m;
// 隣り合う2点のベクトルと距離を算出 ベクトルに直行する平面の回転角を算出
float3 vec = normalize(ppos[tid+1] - ppos[tid]);
float len = length(ppos[tid+1] - ppos[tid]);
float3 axis = normalize(cross(vec, float3(0,1,0)));
float theta = acos(dot(vec, float3(0,1,0)));
// 両端の状態で色を決定
float2 cuv = float2(0.65 - 0.1 * (Booth[tid] - 1) * (Booth[tid+1] - 1), 0.166 * gid + 0.083);
[unroll]
for ( int n = 0; n < 4; n++ ) {
[unroll]
for ( int q = 0; q < 2; q++ ) {
//始点の2点を生成
float3 tpos = mul(QuaternionToMatrix(axis, theta), sqVtx[n + q] * _Thickness) + ppos[tid];
o.vertex = float4(tpos, 1.0);
o.vertex = UnityObjectToClipPos(o.vertex);
o.uv = cuv;
stream.Append(o);
//終点の2点を生成
float3 tpos2 = tpos + vec * len * step(0.5, Booth[tid+1]);
o.vertex = float4(tpos2, 1.0);
o.vertex = UnityObjectToClipPos(o.vertex);
o.uv = cuv;
stream.Append(o);
}
stream.RestartStrip();
}
}
}
fixed4 frag (g2f i) : SV_Target
{
float4 col = tex2D (_MainTex, i.uv) * _Color;
return col;
}
ENDCG
}
}
}いいなと思ったら応援しよう!

