
複素数を用いた交流回路の計算方法について(考え方)
この記事では、交流回路を複素数を用いて、どのように考えるかについてまとめてみました。
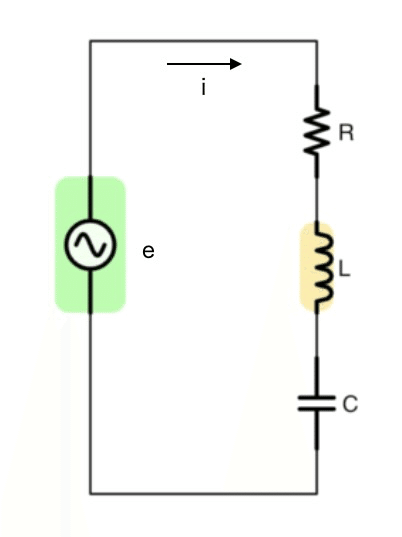
まず図1のようなRLC直列回路を考えます。
今、この回路に流れる電流の瞬時値を
$${i(t)=I_m\sin(\omega t-\theta)\hspace{185pt}(1)}$$
とすると、電圧の瞬時値は
$${e(t)=Ri(t)+L\frac{di(t)}{dt}+\frac{1}{C}\int i(t)dt\hspace{130pt}(2)}$$
$${=RI_m\sin(\omega t-\theta)+L\frac{d}{dt}\{I_m\sin(\omega t-\theta)\}+\frac{1}{C}\int I_m\sin(\omega t-\theta)dt\hspace{15pt}(3)}$$
ここで、このまま計算するか、複素数を用いて計算するかに分かれるのですが、ここでは、複素数を用いた方法を考えます。
複素数を用いて計算するために、以下のオイラーの公式を利用します。
$${e^{j\theta}=\cos\theta+j\sin\theta\hspace{40pt}(j=\sqrt{-1})\hspace{110pt}(4)}$$
$${\theta}$$の部分を$${\omega t-\theta}$$に置き換えると
$${e^{j(\omega t-\theta)}=\cos(\omega t-\theta)+j\sin(\omega t-\theta)\hspace{120pt}(5)}$$
と書くことができ、この式の虚部に着目すると、(3)式の$${\sin(ωt-θ)}$$部分と同じであることが分かります。
今、(3)式の$${\sin(ωt-θ)}$$部分をオイラーの公式を用いて指数関数に変換してしまえば、計算が簡単になると思いませんか?
なぜなら、指数関数eは微分しても積分しても形が変わらないからです。
但し、オイラーの公式で使用するのは、虚部のsinの項だけで、実部のcosの項は使用しません。
(2)式ではsinの項しかありませんが、cosの項があるものとしてオイラーの公式を用いて変換します。
計算が終わった後に、虚部のsinの項のみを書きます。
今、(2)式をオイラーの公式を用いて指数関数表記に変換すると、
$${e(t)=RI_me^{j(\omega t-\theta)}+L\frac{d}{dt}I_me^{j(\omega t-\theta)}+\frac{1}{C}\int I_me^{j(\omega t-\theta)}dt}$$
$${=RI_me^{j(\omega t-\theta)}+j\omega LI_me^{j(\omega t-\theta)}+\frac{1}{j\omega C}I_me^{j(\omega t-\theta)}}$$
$${=RI_me^{j(\omega t-\theta)}+j\omega LI_me^{j(\omega t-\theta)}+\frac{1}{j\omega C}\cdot\frac{j}{j} I_me^{j(\omega t-\theta)}}$$
$${=RI_me^{j(\omega t-\theta)}+j\omega LI_me^{j(\omega t-\theta)}-\frac{j}{\omega C}I_me^{j(\omega t-\theta)}}$$
$${=\{R+j(\omega L-\frac{1}{\omega C})\}I_me^{j(\omega t-\theta)}\hspace{100pt}(6)}$$

今、(6)式において複素数Zを考え、
$${Z=R+j(\omega L-\frac{1}{\omega C})}$$
とすると
$${Z=|Z|\biggr\{\frac{R}{|Z|}+\frac{1}{|Z|}j(\omega L-\frac{1}{\omega C})\biggr\}}$$
$${=\sqrt{R^2+(\omega L-\frac{1}{\omega C})^2}\biggr\{\frac{R}{\sqrt{R^2+(\omega L-\frac{1}{\omega C})^2}}+\frac{1}{\sqrt{R^2+(\omega L-\frac{1}{\omega C})^2}}j(\omega L-\frac{1}{\omega C})\biggr\}}$$
今、複素平面上において
$${\frac{R}{|Z|}=\cos\varphi}$$
$${\frac{\omega L-\frac{1}{\omega C}}{|Z|}=\sin\varphi}$$
$${\varphi=\tan^{-1}\frac{\omega L-\frac{1}{\omega C}}{R}}$$
の関係があるので
$${Z=|Z|(\cos\varphi+j\sin\varphi)}$$
$${=|Z|e^{j\varphi}}$$
そうすると(6)式は
$${e(t)=|Z|e^{j\varphi}I_me^{j(\omega t-\theta)}}$$
$${=\sqrt{R^2+(\omega L-\frac{1}{\omega C})^2}I_me^{j(\omega t-\theta+\varphi)}}$$
$${=\sqrt{R^2+(\omega L-\frac{1}{\omega C})^2}I_m\{\cos(\omega t-\theta+\varphi)+j\sin(\omega t-\theta+\varphi)\}}$$
ここで、虚部のsinの項のみを取ると
$${e(t)=\sqrt{R^2+(\omega L-\frac{1}{\omega C})^2}I_m\sin(\omega t-\theta+\varphi)\hspace{100pt}(7)}$$
この様に、オイラーの公式を用いて、回路の計算を行うことができます。
ただし、この計算方法で求めることが出来る解は、回路のスイッチを入れてから時間が経った定常状態における電流の値です。
(7)式は定常項のみです。スイッチを入れた瞬間に流れる過渡的な電流値の項は含まれていません。
過渡的な電流値の項を含んだ解を求めるためには、(3)式の微分方程式を真面目に解く必要があります。
ここでのポイントは以下になります。
今、オイラーの公式を用いて、回路に流れる電流の瞬時値を次のように表すことができました。
$${i(t)=I_m\sin(\omega t-\theta)=I_m e^{j(\omega t-\theta)}}$$
今、電源電圧の瞬時値は
$${e(t)=RI_me^{j(\omega t-\theta)}+j\omega LI_me^{j(\omega t-\theta)}+\frac{1}{j\omega C}I_me^{j(\omega t-\theta)}}$$
で表され、簡略化のためにi(t)=I、e(t)=Eと置くと、
$${E=RI+j\omega LI+\frac{I}{j\omega C}}$$
この式において、jω倍することは電流の瞬時値を微分することと等価、1/jω倍することは電流の瞬時値を積分する事と等価であることがポイントです。
指数関数eは微積分によって形が変わらないので、この様に複素数表記で計算を行い、計算が終了したらIを最初の電流の瞬時値表記に戻すだけで良いことになるのです。
三角関数の微積分を含んだ、やや複雑な式であったものが、オイラーの公式を用いて複素数表記に変換してしまえば、簡単な代数式の計算を行うだけで良いことになるのです!
最後まで読んでいただき、ありがとうございます。
この記事が気に入ったらサポートをしてみませんか?
