
PRML:1.2節(確率論)の紹介(PART2)
『パターン認識と機械学習(上)』というあの黄色本を用いてゼミを行った際の発表資料をnoteにもアップすることにしました。noteにはゼミ資料を再編集したものをアップします。
本ノートでは、1.2節の発表資料の一部(1.2.1節と1.2.2節)をアップし、コメントを記します。資料はできるだけ原著に忠実に作成することを心がけていますが、本noteは、原著だけでなく、自分自身が感じていることも含めてまとめています。
↓1.2.1節と1.2.2節関連のスライドはこちらです。
↓1.2節のイントロについてまとめたnote記事はこちらです。
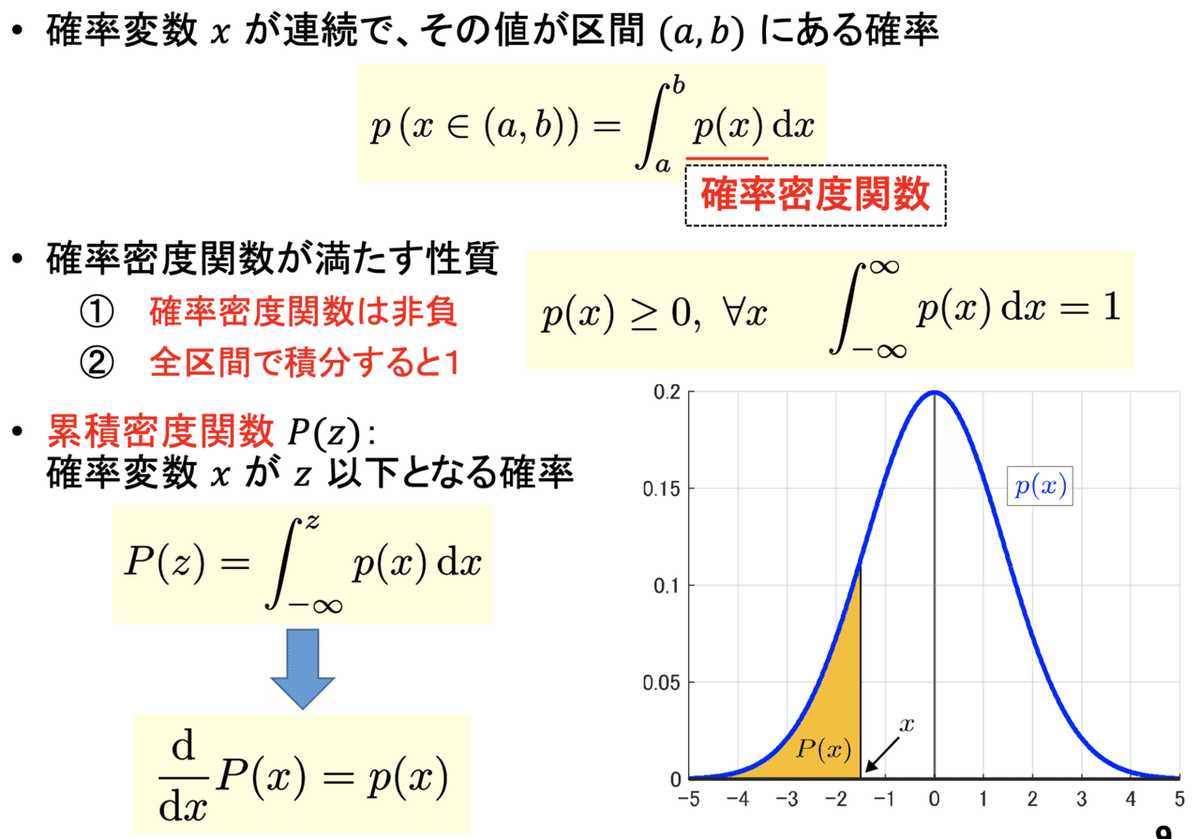
確率密度関数
確率変数xが連続の場合には「確率密度関数」を考えます。確率変数xの値が区間(a,b)(a<x<b)となる確率を、確率密度関数のaからbまでの定積分として考えます。
確率密度関数の特徴は「全空間で非負の関数である」ことと、「全区間で積分すると1になる」ことです。注意しなければならないこととして、確率密度関数は1を超えても良いということがあります。積分値が1となることと、確率密度関数が全区間で1を下回ることは等価ではありません。
累積密度関数 P(z) は「確率変数xがz以下となる確率」として定義されます。微分積分学の基本定理から、累積密度関数の微分は確率密度関数に一致します。
確率密度関数の変数変換
PRMLの1.2.1節では「確率密度関数の変数変換」の公式が紹介されています。ここでは具体例まで踏み込んでいません。例えば、カイ二乗分布の密度関数は、ガウス分布の密度関数から変数変換を利用して導出することができます。カイ二乗分布の密度関数の導出は以下のサイトなどを参照してください。
多次元の確率密度関数の変数変換ではJacobianが出てきて、一気に難しくなります。見た目も難しくなり、計算も難しくなります。行列式を計算できないと変数変換後の密度関数の形を陽に記述できないのは課題でもあります。そのため、実用的にはJacobianが計算できる場合しか考えることができません。

期待値
1.2.2節では期待値と分散について、その定義が記されています。期待値は確率分布からサンプルした値がどんな値になることが期待されるかを表す、確率分布を特徴づける量の1つです。
得られたデータが従う分布を特徴づける量として、「期待値(平均値)」「中央値」「最頻値」がよく使われます。期待値は極端に大きな値などの外れ値に引っ張られる傾向があることに注意する必要があります。
真の確率分布から得られたデータだけが手元にある場合は、得られたデータの単なる平均値で、真の期待値を近似することがあります。これが妥当であるかどうかは、統計分野の「推定量」の概念と関係があります。「最尤推定量」や「不偏推定量」の話を参照してみてください。

分散と共分散
分散は確率分布の期待値のまわりの散らばりを表す量です。分散も確率分布を特徴づける量の1つです。分散の正の平方根が標準偏差であり、これも確率分布を特徴づける量として利用されます。
正規分布(1.2.4節で登場)で分布を近似できる場合、データの約68%が「期待値±標準偏差」の範囲(1シグマ範囲)にあることが知られています。
共分散は2つの確率変数の関係を記述する量です。確率変数xとyが独立であるならば、共分散は0になります。

※本資料はGithubにもアップロードしています。本ノートおよびアップロードしている資料について何かありましたら、noteのコメント欄までお願いします。
この記事が気に入ったらサポートをしてみませんか?
