電気

この記事は途中です。

また、この記事を鵜吞みにすると、お家が燃えたり試験に落ちます。

直流

時間に伴って電圧および電流のプラスマイナスが変化しないもの。また、簡単に考えたい時など、プラスマイナスだけでなく大きさ自体が変化しない電圧（定電圧）および電流（定電流）を指して直流と称されることもある。電池が代表。また、理想。
逆に言うなら、電圧および電流が脈打っていても、プラスマイナスが変化しなければそれは直流である。下記の交流を変換操作して直流を得る場合、こうした脈動する直流が得られる場合がある。

交流

時間に伴って電圧および電流のプラスマイナスが交互に入れ替わるもの。モーターは電気を流すとぐるぐる回るが、逆に物理的な力（水、風、蒸気など）でもって物理的にぐるぐる回すと電気を生ずる発電機となる。これをそのままとりだすと交流となる。詳細は後。

オームの法則まわり

クーロンの法則まわり

ガウスの法則

$$
\oint_S \varepsilon \mathbf{E} \cdot d\mathbf{S} = \oint_S \mathbf{D} \cdot d\mathbf{S} = \int_V \rho \, dV = Q
$$

E : 電場
ε : 誘電率
D : 電束密度
ρ : 電荷密度
Q : 電荷
dS : 面素ベクトル
V : 体積

ある面を覆う微小面らに対し、各微小面に紐付けられた面積ベクトルとベクトル場である電場との内積の総和の極限をとる。

インテグラルは総和というか総和の極限扱いで良い。
微小変位は比較的自由に実数的に扱ってよいが、インテグラル単体はそれ自体では意味がなく、あくまで微小変位（積分変数）とセットでないと機能しない。
インテグラル内積は内積の右っかわが暗黙のうちに積分変数である。
これは例えば$${\int f(x)dt}$$が積分変数$${dt}$$との積の総和の極限であると考えるなら、積の親戚である内積の総和の極限も$${\int \mathbf{E} \cdot d\mathbf{S} }$$でよかろうということである。

だもんで

$$
\oint_S \varepsilon \mathbf{E} \times d\mathbf{S}
$$

こういう表記もありえる（多分）。

電場を球状に捉える場合、微小面積 $${dS}$$ の総和の極限 $${\int_S dS}$$ は球の表面積 $${4\pi r^2}$$ である。単位面積当たりの電場の強さを$${E}$$ とするなら、球の表面から湧き出す電場のフラックスの大きさは $${\int_S\varepsilon E dS = \varepsilon E \cdot 4\pi r^2}$$ となる。

ガウスの法則はクーロンの法則における電荷の湧き出す形状$${4\pi r^2}$$を一般化$${\int d\bm S}$$にしたもの。任意形状に対する電場則がガウスの法則。

電場とその出力ベクトルの意味するところは、単位面積当たりの電荷全部足して、結果その任意形状が湧き出してるか吸い込んでるかを示すもの。

あるいはある電荷からみて周囲電荷の分だけ$${q_i\times\bm r_i}$$全部足して表面積で割ったものは電場の強さである。

単位面積当たりの電荷$${\frac{Q}{dS}}$$(球なら$${\frac{Q}{4πr^2}}$$。これは電束密度$${D=\frac{Q}{4πr^2}}$$であって、単位面積あたりの電束の数である)

単位面積当たりの電荷を全部足すを球でやると

$$
\mathbf E(\mathbf r)=\frac{1}{4\pi r_i^2}\sum q_i \mathbf n_i
$$

ただし$${Q=\sum q_i}$$

球なら電荷の位置が全部等距離にあるから$${r}$$にインデックスはいらない。

逆に電荷が球状に分布せず、どっか遠くにあったとする。
この場合でもその電荷と結ばれる直線上のある距離$${r}$$地点での影響を考えるなら、そこに仮想的な電荷があると考えて結局全部等距離に並べることができると前向きに考える。インデックスをとって

$$
\mathbf E(\mathbf r)=\frac{1}{4\pi r^2}\sum q_i \mathbf n_i
$$

ここで$${\mathbf n_i=\frac{\mathbf r-\mathbf r_i}{|\mathbf r-\mathbf r_i|}}$$
であって、これも全部等距離であるなら
$${\mathbf n=\frac{\mathbf r}{|\mathbf r|}}$$
したがって電荷が全部等距離という前提において

$$
\mathbf E(\mathbf r)=\frac{1}{4\pi r^2}\sum q_i \mathbf n
$$

であって、等距離の成す表面積は球$${S=4\pi r^2}$$であるから
$${\mathbf{q}_i=q_i \mathbf{n}_i}$$とするなら

$$
\mathbf E(\mathbf r)=\frac{1}{4\pi r^2}\sum \mathbf q_i=\frac{1}{S}\sum \mathbf q_i
$$

$${Q=\sum q_i}$$であったから$${\mathbf Q=\sum \mathbf{q}_i}$$

よって

$$
\mathbf E(\mathbf r)=\frac{\mathbf Q}{S}
$$

であってその大きさは

$$
|\mathbf E(\mathbf r)|=E(\mathbf r)=\frac{Q}{S}
$$

この式に比例定数である透磁率$${\varepsilon }$$を追加すると立派なガウスの法則となる。

この単純化された式だけでみると、電場は周囲の大小さまざまであろう電荷の影響を単位面積で割った平均。単位面積当たりの電荷ベクトル。

ガウスの定理

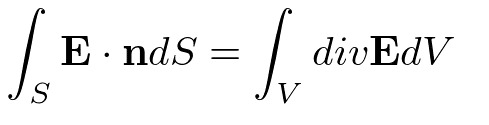
nは単位法線ベクトル。ある面Sに垂直かつ長さ1のベクトル。
単位ベクトルと内積をとると、単位ベクトル方向の成分（落とした影の長さ）が抽出できる。

ベクトル場である電場（単位面積当たりから飛び出して向き・大きさ共に不明というか自由なベクトル）を単位面当たりの法線方向に固定する操作。

電気回路

磁気

超おおざっぱに

そも磁石とはなにか。
電荷の担い手たる電子というのはそれ自体磁石みたいなもんである。
ある種の金属は磁石みたいな電子が死ぬほど余るので磁石となる。
条件次第で磁石になったりならなかったりする磁石は磁石みたいになった電子がきっちり揃ったり揃わなかったりするやつである。

磁力の影響は
磁石で遊ぶことで露骨に明確に目で見ることができる。
電流によって生じることが実験によって確かめることができる。
電気のように直接くらってビリビリすることはできない。

電荷の場合は正と負があり、各々独立に存在しえた。磁石の場合はS極とN極があるが、各々単独には存在しえない。電気と磁気、電荷と磁荷は極めて似たような性質を持つし、比較もされるし並べられるし、その方が説明しやすかったり理解しやすかったりもするのだが、決して同じものにはならない。

例えば磁荷を単独で扱っているかのように説明しているときも、ちゃんとS極N極がセットであることは覚えておかなければならない。

磁石の単位はテスラ(Wb/m^2)

磁荷

磁気、磁力の元。単位はウェーバ。真空中で１ｍ離れた磁荷同士に働く力が6.33×10^4[N]である時、1[Wb]とする。磁石の戦闘力の元。

磁荷のクーロンの法則

これは単純に考えるなら磁石と磁石の殴り合いの話である。

あるいは

ただし

μは透磁率。μ_rは比透磁率。真空中ではμ_r=1。μ_0を真空中の透磁率(=4pi*10^-7[H/m])とすると。

再掲：電荷のクーロンの時の誘電率まわり。

磁場（磁界）

磁荷に対して力を及ぼす空間。これはつまり片方の磁石を固定し、その周辺にもう一つ磁石を置いた時にその磁石にかかる力の話である。磁石界の霊圧に等しい。

基準となる磁荷による磁気が働く範囲。ベクトル場。この空間中に磁荷を置くと、磁荷には力（大きさと向き）が発生する。磁界中に1[Wb]の磁荷を置き、この磁荷に1[N]の力がかかる時、この磁界は1[A/m（アンペア毎メートル）]の強さを持つ。

H[A/m]の磁界中にm[Wb]の磁荷を置くと、この磁荷にかかる力[N]は

アンペール則

アンペア毎メートル

１メートル離れた磁荷間の起磁力が１アンペア（アンペア回数）である磁場の強さ。

アンペアあるいはアンペア回数（アンペアターン, ampere-turn, AT）

コイル１巻きに直流の電流を流した時の起磁力の単位。
アンペア×巻数なので電流のアンペアとまったく同じというわけではない。
メートルと平方メートルが違うくらいには違う。
とはいえ、磁荷に仕事をさせるには電気が始まりとなることは分かる。

起磁力(magnetomotive force, MMT)

磁気回路に磁束を生じさせる力。
電気回路では電圧及び起電力に相当する。
磁気回路の場合、電流に相当するのは磁束。

アンペールの法則により起磁力F[AT]は以下。ただしNはコイルの巻数。Iは電流。ここでのFはニュートンではない。

$$
F=NI
$$

磁気回路のオームの法則（ホプキンソンの法則）
Φは磁束。Fはアンペアターン。

$$
F=\phi R
$$

また磁場Hおよびソレノイド長Lで表すと

$$
F=HL
$$

一般化すると

$$
\bm F=-\int \bm H\cdot d\bm l
$$

やはりFはアンペアターン。

その一方、電気回路における起電力は以下の形。

$$
\bm V=-\int \bm E\cdot d\bm l
$$

内積インテグラルはインテグラルが単体で出現しているみたいに見えて気持ち悪いが、内積の右っ側に積分変数があるので、総和の極限として十分機能する。

つまり

$$
\bm V=-\int \bm E\cdot d\bm l =-\lim\limits_{N \rightarrow \infty}\sum\limits_{i=1}^{N} \bm E\cdot d\bm l
$$

区間を無限に増やすことで変位が限りなくゼロに近づく。

磁力線

1[Wb]の磁荷から真空中で$${\frac{1}{μ_0}}$$本。比透磁率$${μ_r}$$の物質では$${\frac{1}{μ_0μ_r}}$$本でると考えると便利なもの。磁力線の$${\frac{1}{μ}}$$本の束を磁束とする。ただしμは透磁率。

$$
\mu=\mu_0\mu_r
$$

磁束

磁場の強さと向きに関して1[Wb]を１本とみたもの。Bは磁束密度。Sは面積要素。

$$
\phi = -\int_S \bm B\cdot d\bm S
$$

磁束密度

磁束の単位面積当たりの面密度。単位はテスラ[T]

$$
B=\mu H
$$

磁場Hは電流Iおよび力F、および磁束密度Bと繋がっており、起磁力は磁場Hおよび電流Iからひねり出される。また、起磁力は磁束を生み出し、磁束はほかのいろんなもんからも生成される。

交流

波の基本

回転運動は波に変換できる。発電機というのは回転運動から電気を取り出すため、取り出された電気は波となる。円の回転から取り出された波はsin関数にだいたい従う。sin関数は角度を入力すると-1から+1までを出力する三角形の辺の長さの比である。

例えば車のタイヤについたガムは、タイヤを回転させるとぐるぐる回る。これを車の正面から見ればガムは上下運動していることになる。この上下運動を時間を横軸にプロットすると波になる。図はぐぐるとでる。

正弦波交流の場合。

交流の電圧ないし電流は時間に応じてプラスにマイナスにと脈打つため、全体を代表するような数値を使わないとやってられない。そのような代表値を実効値という。

例えば電圧の実効値は全体の最大値を用いて

とあらわされる。

時間に応じて脈打つような一瞬一瞬の値を瞬時値といい、
電圧の瞬時値は全体の最大値を用いて

ただしE_maxは電圧の最大値。実効値Eであらわすと

E_maxは波においては振幅に相当する。ωは角周波数[rad/s]、ωtで位相[rad]。

角速度

周波数

角速度は単位時間あたりに進む角度、向きと大きさをもつベクトル量であるが、角周波数はその大きさである。死ぬほどおおざっぱに考えると回転速度であり、数式的には2π秒間に波がぷるぷるする回数、2π秒間の回転数である。

また、1秒間にf回転すると考えると
速度=距離/時間から
ω=2π/(1/f)
1周(2π)を周期(秒)で回る速度

vは回転軸に直交する方向への速度[m/s]
rは回転半径[m]
Tは周期であり、波が一周する時間である。

fは周波数。周期の逆数。１秒間に波がぷるぷるする回数。円状に考えると１秒間の回転数。

実効値

実効値(effective value, root mean square value, RMS)
電圧および電流の二乗平均平方根(Root Mean Square)

二乗平均平方根とはなにか
与えられた入力データを二乗し、算術平均（総和してデータ数で割る）をとり、平方根をとったもの。
期待値からの偏差に対して二乗平均平方根をとると標準偏差（分散の平方根）が得られる。実効値は期待値を０とみなした時の標準偏差。

なぜ二乗するか
二乗してない値を（算術平均のために）そのまま足すとプラスとマイナスが打ち消しあって値が消滅するため。二乗して符号を統一している。

絶対値ではダメか
計算しづらい。

なぜ平方根か
例えば電圧の単位は[V]であるが、値を二乗すると[V^2]となり、意味が変わる。メートルと平方メートルくらい意味が変わる。平方根をひっかけることで[V]に戻る。

入力データが離散値でなく連続値である場合は総和の代わりに積分を用いることになる。特に周期関数の場合はデータ数の代わりに周期で割ることになる。

コイルとコンデンサ

交流回路

$$
\begin{aligned}
v_L(t) &= L \frac{\Delta i(t)}{\Delta t} \\
i(t) &= \frac{1}{L} \int v_L(t)dt\\
v_C(t) &= \frac{1}{C} \int i(t)dt \\
i(t) &= C \frac{\Delta v_C(t)}{\Delta t} \\
v_R(t) &= Ri(t) \\
i(t) &= \frac{v_R(t)}{R} \\
\end{aligned}\\
$$

あるいは

$$
v_L(t) = L \frac{d i(t)}{d t} \\
v_L(t)dt = L d i(t) \\
\int v_L(t)dt=\int Ldi(t)\\
\int v_L(t)dt=\int L\frac{di(t)}{dt}dt\\
\int v_L(t)dt=Li(t)\\
i(t) = \frac{1}{L} \int v_L(t)dt
$$

微小変位$${di, dt}$$なんかを実数扱いして移項したり、
インテグラルを単独で用いたりはやってもいいけど
きちんとした意味を持つのは
インテグラルと微小変位で挟んだ積分と
微小変位の比で表した微分だよの意味。
特に積分インテグラル単体は近似計算ならシグマとみなせばよいが
そうでないなら微小変位とセットでないとなんともみなせない状態になる。
微小変位が文脈的にあきらかならそれは省略でき、総和の極限とみなせばその単独インテグラルは許されるであろう。逆に、積分変数が迷子なら単独インテグラルは許容されない。物理で出てくる内積とセットのインテグラルは、内積の右っ側が積分変数となっておって、これのおかげでインテグラルが迷子にならない。だから許されてるしいきなりでてくる。
微分だけなら比較的自由に微小変位はうろちょろできる。

RLC直列回路は

$$
\begin{aligned}
v_1 + v_2 + v_c &= e(t) \\
L \frac{di(t)}{dt} + Ri(t) + \frac{1}{C} \int i(t)dt &= e(t)
\end{aligned}
$$

ただしeは時間に応じて変化する電源電圧。

あるいは$${i=c \frac{v}{t}}$$ を利用して

$$
\begin{aligned}
L \frac{d}{dt} C \frac{dv_c(t)}{dt} + RC \frac{dv_c(t)}{dt} + \frac{1}{C} \int C \frac{dv_c(t)}{dt} dt &= e(t) \\
LC \frac{d^2v_c(t)}{dt^2} + RC \frac{dv_c(t)}{dt} + v_c &= e(t)
\end{aligned}
$$

位相が遅れる

交流回路の素子は電圧や電流に対して時間による微分をとるため、電圧や電流の式にsinやcosをとると微分されてsin,cosが入れ替わる。これをもって

インダクタンス回路では電流は電圧よりpi/2(90度)遅れる
あるいは電圧は電流よりpi/2進むといい
(ELI エリー 電圧インダクタンス電流)

コンデンサ回路ではでは電圧は電流よりpi/2(90度)遅れる
あるいは電流は電圧よりpi/2進むという。
(ICE アイス 電流コンデンサ電圧)

商用電源周波数（お家のコンセントにかかる交流電圧の周波数）は東日本で50Hz、西日本では60Hz。これは1秒間に50回ないし60回、波が振幅するということで、波というのは同じ形の繰り返しとみなされるものであるから、sin,cosの波ならだいたい真ん中から上いって下いって真ん中に戻ったら1周である。

50Hzなら1秒間に50周する。すなわち1周するのに0.02秒。
60Hzなら1秒間に60周する。すなわち1周するのに0.0166666...秒。

波の1周が2*piであるから、pi/2(90度)遅れるとは1/4周遅れるということ。
発電機でもってコイルをくるくる回して交流電圧電流を作っている以上はこの定めからは逃れられない。

50Hzなら0.02/4=0.005秒遅れる。
60Hzなら1/60/4=0.00416666...秒遅れる。

インピーダンス

交流回路の抵抗成分。
直流回路の抵抗と、コイルの抵抗成分である誘導性リアクタンス、コンデンサの抵抗成分である容量性リアクタンスからなる。

誘導性リアクタンス

コイルのインダクタンスLに起因する抵抗成分。

$$
X_L=\omega L=2\pi fL
$$

ωは角速度、fは周波数。
コイルは、周波数が高くなると交流に対する抵抗が高くなる。
直流回路の抵抗と違い、エネルギーを消費しない。電源から与えられたエネルギーを磁界に変換して蓄え、また電源に戻す。

容量性リアクタンス

コンデンサの静電容量Cに起因する抵抗成分。
コンデンサは周波数が高くなると交流に対する抵抗が低くなる。
エネルギーを消費しない。電源から与えられたエネルギーは電池の要領で充電され、また電源に戻る。

$$
X_C=\frac{1}{\omega C}=\frac{1}{2\pi f C}
$$