ベクトル解析(メモ)
この記事は理解のベクトルがあさっての方向に向いている可能性がなきにしもあります。
前準備
この辺の感覚もいります。
参考図書
道具としてのベクトル解析 単行本 – 2017/6/29
涌井 貞美 (著)
大学演習 ベクトル解析(矢野健太郎、石原繁 共著) 大学演習新書 Kindle版
矢野 健太郎 (著), 石原 繁 (著)
方向余弦(l,m,n)
参考
p19-, ベクトル解析 (理工系の数学入門コース 新装版) 単行本 – 2019/11/15
戸田 盛和 (著)
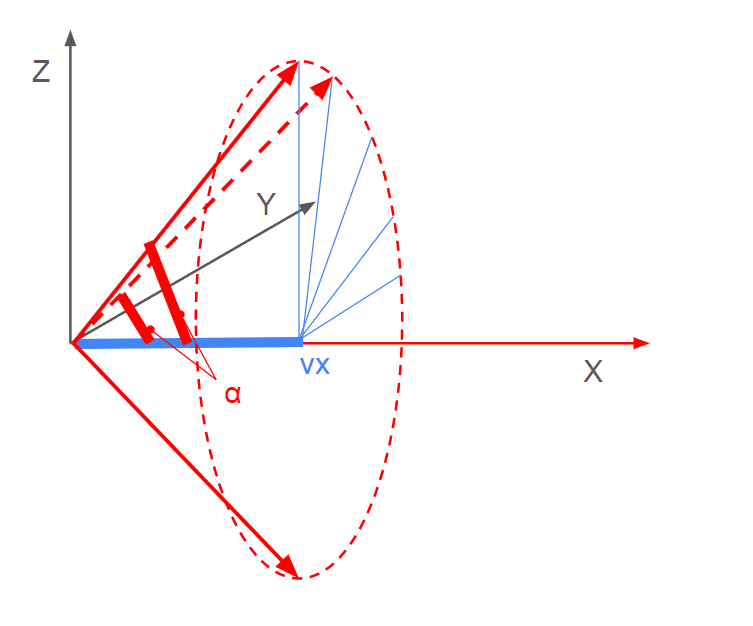
方向余弦(Direction Cosines)は、空間内のベクトルが、基準とする座標軸に対してどのような角度で配置されているかを表す指標です。これは、ベクトルと各座標軸(通常、x軸、y軸、z軸)との間の角度の余弦(cosine)で定義されます。方向余弦は、ベクトルの方向を定量的に理解するのに役立ちます。簡単にいうとただの$${cos}$$です。
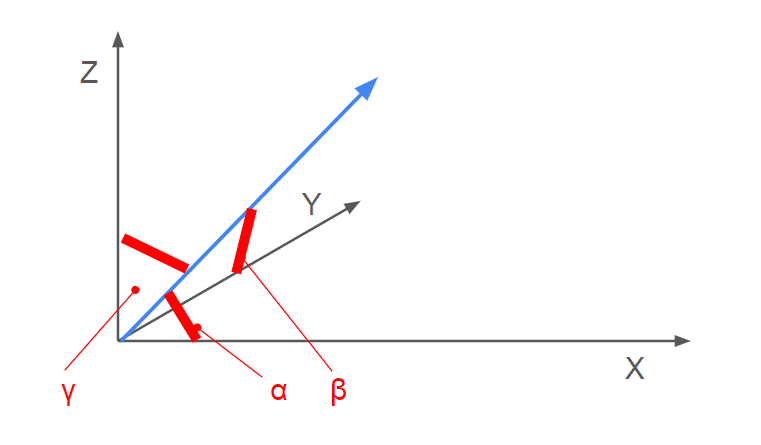
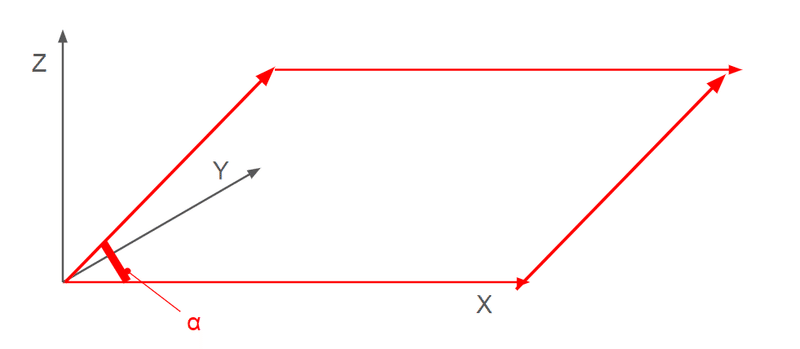
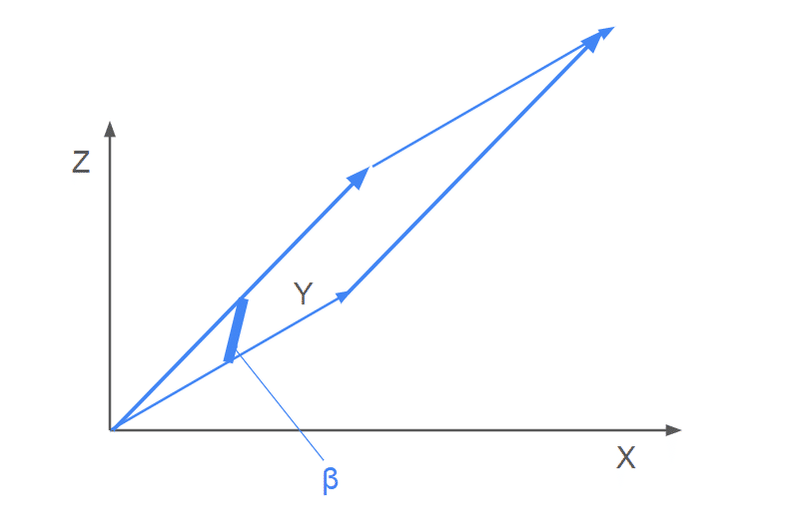
定義と計算方法
あるベクトル $${\mathbf v(v_x,v_y,v_z) }$$ が空間内にあるとき、そのベクトルとx軸、y軸、z軸との間の角度をそれぞれ $${\alpha}$$、$${\beta}$$、$${\gamma}$$ とします。このとき$${\mathbf{v}}$$ の方向余弦は、以下のように定義されます。
$${l = \cos\alpha}$$:ベクトル $${\mathbf{v}}$$ とx軸との間の角度の余弦。
$${m = \cos\beta}$$:ベクトル $${\mathbf{v}}$$ とy軸との間の角度の余弦。
$${n = \cos\gamma}$$:ベクトル $${\mathbf{v}}$$ とz軸との間の角度の余弦。
$$
l = \cos \alpha = \frac{v_x}{|\mathbf v|}, \quad m = \cos \beta = \frac{v_y}{|\mathbf v|}, \quad n = \cos \gamma = \frac{v_z}{|\mathbf v|}
$$
$${ l^2 + m^2 + n^2 = 1 }$$
この時ベクトル $${\mathbf v (v_x,v_y,v_z)}$$の各々の成分は、ベクトル $${\mathbf v}$$の各軸へ落とす影、正射影の大きさであって
$$
v_x = |\mathbf v| \cos \alpha, \quad v_y = |\mathbf v| \cos \beta, \quad v_z = |\mathbf v| \cos
$$
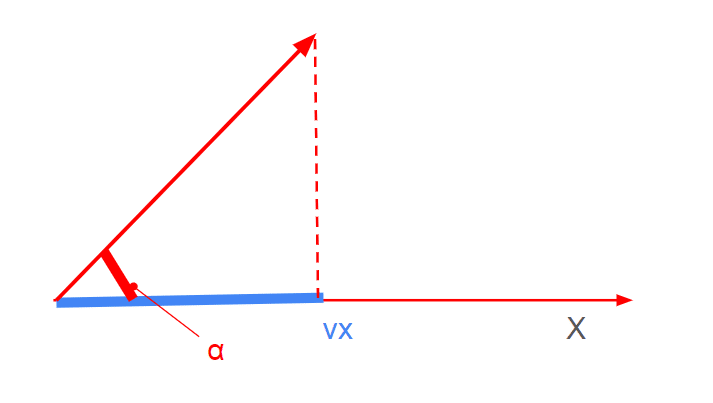
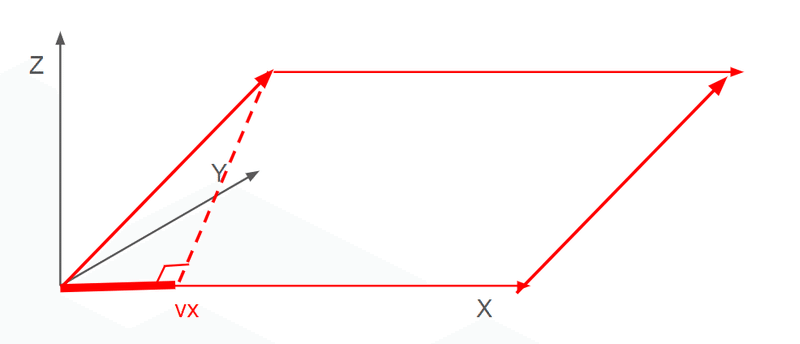
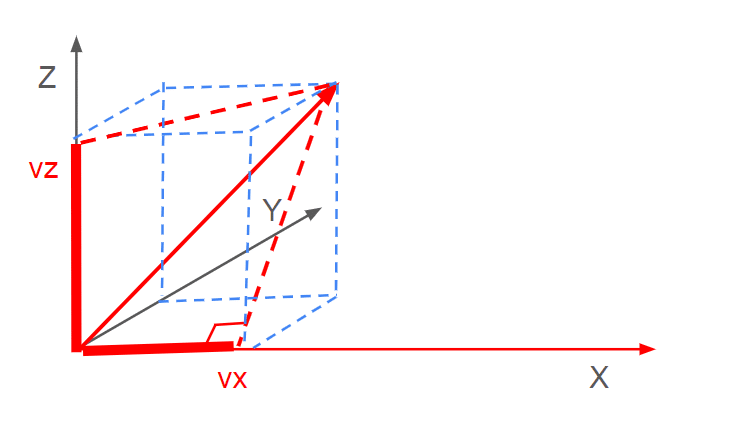
方向余弦を用いて表すと
$$
v_x = |\mathbf v|l, \quad v_y = |\mathbf v|m, \quad v_z = |\mathbf v|n
$$
あるベクトル$${\mathbf v}$$を基底と方向余弦を用いて表すと
$$
\mathbf v=|\mathbf v|l\bold i +|\mathbf v|m\bold j+|\mathbf v|n\bold k\\
\mathbf v=|\mathbf v|(l\bold i +m\bold j+n\bold k)\\
\mathbf v=|\mathbf v| \bold i \cos\alpha+|\mathbf v|\bold j \cos\beta+|\mathbf v|\bold k\cos\gamma\\
\mathbf v=|\mathbf v| (\bold i \cos\alpha+\bold j \cos\beta+\bold k\cos\gamma)\\
$$
ベクトル$${\mathbf v}$$の単位ベクトルは
$$
\hat{\mathbf v}=\frac{\mathbf v}{|\mathbf v|}=l\bold i +m\bold j+n\bold k=\bold i \cos\alpha+\bold j \cos\beta+\bold k\cos\gamma
$$
内積$${\bm A\cdot \bm B=|\bm A||\bm B|\cos\theta=A_xB_x+A_yB_y+A_zB_z}$$を用いると、
$$
\cos\theta=\frac{1}{|\bm A||\bm B|}(A_xB_x+A_yB_y+A_zB_z)
$$
ベクトル$${\bm A}$$の方向余弦を$${l_1, m_1, n_1}$$とし、
ベクトル$${\bm B}$$の方向余弦を$${l_2, m_2, n_2}$$とするなら
$$
A_x=|\bm A|l_1, A_y=|\bm A|m_1, A_z=|\bm A|n_1\\
B_x=|\bm B|l_2, B_y=|\bm B|m_2, B_z=|\bm B|n_2\\
$$
$$
l_1^2+m_1^2+n_1^2=l_2^2+m_2^2+n_2^2=1
$$
よって
$$
\cos\theta=\frac{1}{|\bm A||\bm B|}(A_xB_x+A_yB_y+A_zB_z)\\
=\frac{1}{|\bm A||\bm B|}(|\bm A|l_1|\bm B|l_2+|\bm A|m_1|\bm B|m_2+|\bm A|n_1|\bm B|n_2)\\
=l_1l_2+m_1m_2+n_1n_2
$$
ベクトル値関数
$${t}$$を実数のパラメータ、
$${\bold i, \bold j, \bold k}$$を基底、
ベクトルとその成分を$${\bm A(f_1,f_2,f_3)}$$とすると、
$${\bm A}$$が$${t}$$に依存する$${\bm A(t)}$$ならば
$${f_1(t),f_2(t),f_3(t)}$$を実数値関数として
$$
\bm A(t)=f_1(t)\bold i +f_2(t)\bold j+f_3(t)\bold k
$$
なる$${\bm A(t)}$$をベクトル値関数、あるいはベクトル関数という。
n次の場合は
$$
\bm A(t)=\sum\limits_{i=1}^{n} f_i(t)\bold e_i=\bm f \cdot \bold e
$$
ただし
$${\bm f}$$は実数値関数の組
$${\bold e}$$は基底ベクトルの組
$${\cdot}$$は内積。
ベクトル値関数は実数とベクトルを対応付ける。
ベクトル場はベクトル値関数の一種である。(p56)
位置ベクトル、あるいは媒介変数曲線の微分(1変数入力ベクトル値関数の微分)
$${f(x)}$$:1変数入力のスカラー値関数の微分は高校で習ういつものやつです。
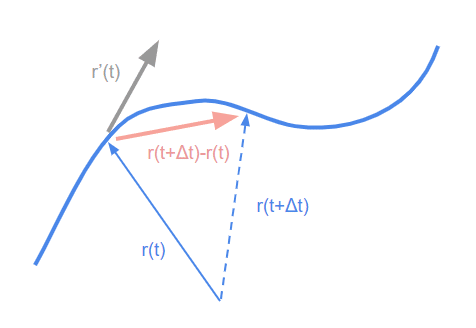
$${\bm r(t)}$$:1変数入力のベクトル値関数の微分は今から説明するものです。位置ベクトルの微分は速度ベクトルであり接線ベクトルです。
$${f(x,y,z)}$$:多変数入力のスカラー値関数の微分は勾配であり関数の最大変化方向であり法線ベクトルです。
多変数入力のベクトル値関数はベクトル場です。微分はヤコビアンです。また、微分相当操作として発散、回転があります。
いつもの微分、導関数は横軸にパラメータ$${x}$$をとり、関数$${f(x)}$$がパラメータ$${x}$$の変位$${Δx}$$(より正確には微小変位$${dx}$$)に応じて変化する量$${f'(x)}$$を得るが、
1変数入力のベクトル値関数の微分の場合は成分関数の導関数の組となる。
例えば1変数入力のベクトル値関数の微分は$${r(t)}$$のどのt地点をとっても$${r'(t)}$$なる、入力の微小な変化に応じた実数値関数の出力の変位の組によるベクトルを返す。それはつまり雑に記すと$${\Delta x, \Delta y, \Delta z}$$であって、正確を期すると$${(\frac{dx}{dt},\frac{dy}{dt},\frac{dz}{dt})}$$である。
1変数入力のベクトル値関数の微分の場合、パラメータtは曲線の始点をt=0,終点をt=1と便利なのでそのように調整されることがある。
また、
ベクトル値関数の微分の結果は接線ベクトル。接ベクトルとも。
$$
\frac{d\bm A}{dt} = \frac{df_1}{dt}\bold i + \frac{df_2}{dt}\bold j + \frac{df_3}{dt}\bold k\\
$$
あるいは往々にして$${t}$$を用いて
$$
\frac{d\bm A(t)}{dt} = \frac{df_1(t)}{dt}\bold i + \frac{df_2(t)}{dt}\bold j + \frac{df_3(t)}{dt}\bold k
$$
また、ベクトル値関数=位置ベクトル$${\bm r(t)}$$の場合は微分すると速度ベクトルとなる。速度ベクトルは接線ベクトルだが、接線ベクトルは必ずしも速度ベクトルとは限らない。
$$
\bm r'(t)=\frac{d\bm r(t)}{dt}= \frac{dx(t)}{dt}\bold i + \frac{dy(t)}{dt}\bold j + \frac{dz(t)}{dt}\bold k=\bm v(t)
$$
速度ベクトルの大きさは速度。速度=1となると単位接線ベクトル。
速度ベクトル=位置ベクトルの微分
$$
\bm v(t) = \frac{d\bm r(t)}{dt}=\bm r'(t)
$$
あるいは成分を係数とし、基底ベクトルを用いて、
速度ベクトルはベクトル値関数
$$
\bm v(t) =v_x(t)\bm i+v_y(t)\bm j+v_z(t)\bm k= \frac{d\bm r(t)}{dt} = \bm r'(t)=\frac{d\bm r(t)}{dt}=\frac{dx(t)}{dt}\bm i+\frac{dy(t)}{dt}\bm j+\frac{dz(t)}{dt}\bm k = \lim\limits_{\Delta t \to 0} \frac{\bm r(t+\Delta t)-\bm r(t)}{\Delta t}
$$
また、位置ベクトルを
$$
\bold r(t)=(x(t),y(t),z(t))
$$
として成分表記した場合、その微分であるところの速度ベクトルは成分関数$${(x(t),y(t),z(t))}$$らの導関数の組となる。
成分表記は暗に基底を省略することに注意する。
$$
\bm v(t) = (v_x(t), v_y(t), v_z(t))= \frac{d\bm r(t)}{dt} = \bm r'(t)=(\frac{dx(t)}{dt},\frac{dy(t)}{dt},\frac{dz(t)}{dt})
$$
あるいは
$$
\bm v(t)
= \begin{pmatrix}
v_x(t)\\
v_y(t)\\
v_z(t)
\end{pmatrix}
= \frac{d\mathbf{r}(t)}{dt}
= \begin{pmatrix}
\frac{dx(t)}{dt} \\
\frac{dy(t)}{dt} \\
\frac{dz(t)}{dt}
\end{pmatrix}
$$
また、位置の(時間の)微分が速度であるなら、
位置の微小変位は速度ベクトルに時間の微小変位を乗じたものになる。
$$
\bm v(t) = \frac{d\mathbf{r}(t)}{dt}\\
d\mathbf{r}(t)=\bm v(t) dt\quad \lbrace\text{距離=速度×時間}\rbrace
$$
ここで位置の微小変位$${d\mathbf{r}}$$は線素ベクトル。その大きさ$${|d\mathbf{r}|}$$は線素。ただし$${dt>0}$$
参考p62, 大学演習 ベクトル解析(矢野健太郎、石原繁 共著) 大学演習新書
位置ベクトルの微小変位$${d \bm r}$$は速度ベクトルに時間の微小変位を乗じたものだが、線素$${ds=|d\mathbf{r}|}$$は速度に時間の微小変位を乗じたもの。
$$
ds=|\bm r'|dt=|d\bm r|=|\bm v dt|=|\bm v|dt=\sqrt{(\frac{dx}{dt})^2+(\frac{dy}{dt})^2+(\frac{dz}{dt})^2}dt=\sqrt{(dx)^2+(dy)^2+(dz)^2}
$$
微小でない$${s}$$は弧長であり曲線の長さである。
曲線が円の場合は$${s}$$は円弧$${s=r\theta}$$である。
速度ベクトルの大きさ=速度
$$
v=|\bm v| = \sqrt{v_x^2 + v_y^2 + v_z^2}=\sqrt{\bm v\cdot \bm v}
$$
$$
v(t) = |\bm{v}(t)| =|\bm r'(t)| =\sqrt{\bm{v}(t)\cdot \bm{v}(t)}=\sqrt{\bm r'(t)\cdot \bm r'(t)}= \sqrt{\left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2 + \left(\frac{dz}{dt}\right)^2}= \sqrt{\left(\frac{dx(t)}{dt}\right)^2 + \left(\frac{dy(t)}{dt}\right)^2 + \left(\frac{dz(t)}{dt}\right)^2}
$$
単位接線ベクトル
位置ベクトル$${\bm r}$$に対し、
接線ベクトル=速度ベクトルは$${\frac{d\bm r}{dt}=\bm v}$$
それの単位ベクトルは単位接線ベクトル
$$
\bm{t} = \frac{\bm v}{|\bm v|}
$$
$${t}$$は時間でも使うがtangentとしても用いられる。
$${\bm r}$$のパラメータが時間$${t}$$でなく弧長$${s}$$ならば、$${ds=|d\bm r|}$$であるから、$${\bm r}$$の$${s}$$に関する微分は単位接線ベクトル
$$
\bm{t} = \frac{\bm v}{|\bm v|} = \frac{d\bm r}{|d\bm r|} = \frac{d\bm r(s)}{|d\bm r(s)|}=\frac{d\bm r(s)}{ds}
$$
速度の積分から位置
速度ベクトルを積分して位置ベクトルを求めるには、速度ベクトルの成分関数をそれぞれ時間$${ t }$$に対して積分します。位置ベクトル$${ \bm{r}(t) }$$は、初期位置$${ \bm{r}(t_0) }$$からの変位を表すため、速度ベクトル$${\bm{v}(t) }$$の積分により求められます。
速度ベクトルが
$$
\bm{v}(t) = \frac{dx(t)}{dt}\bm{i} + \frac{dy(t)}{dt}\bm{j} + \frac{dz(t)}{dt}\bm{k}
$$
の形で与えられているとき、各成分を$${ t }$$に対して積分することで位置ベクトルを得ます。
位置ベクトルの各成分は以下のように計算されます:
$$
x(t) = \int \frac{dx(t)}{dt}dt + C_x \\
y(t) = \int \frac{dy(t)}{dt}dt + C_y\\
z(t) = \int \frac{dz(t)}{dt}dt + C_z
$$
ここで、$${ C_x, C_y, C_z }$$は積分定数であり、これらは初期条件、すなわち$${ t = t_0 }$$における初期位置$${ \bm{r}(t_0) = \bm{r}_0 = (x_0, y_0, z_0) }$$を用いて決定されます。したがって、位置ベクトル$${ \bm{r}(t) }$$は以下の形式で表されます:
$$
\bm{r}(t) = \left( \int \frac{dx(t)}{dt}dt + x_0 \right)\bm{i} + \left( \int \frac{dy(t)}{dt}dt + y_0 \right)\bm{j} + \left( \int \frac{dz(t)}{dt}dt + z_0 \right)\bm{k}
$$
この式により、任意の時刻$${ t }$$における物体の位置を、その速度ベクトルから求めることができます。この過程は、物理学における運動の解析や、工学における軌跡計画など、多岐にわたる分野で利用されます。
定積分
定積分を用いて位置ベクトルを求める場合は、特定の時間区間における速度ベクトルの積分を行います。この方法は、ある時間区間$${ [t_0, t] }$$にわたる物体の変位を求めるのに適しています。初期時刻$${ t_0 }$$における位置ベクトルを$${ \bm{r}(t_0) }$$とし、時刻$${ t }$$における位置ベクトルを$${\bm{r}(t) }$$とすると、位置ベクトル$${ \bm{r}(t) }$$は次のように表されます。
速度ベクトルから位置ベクトルへの変換:
速度ベクトル
$${ \bm{v}(t) = v_x(t)\bm{i} + v_y(t)\bm{j} + v_z(t)\bm{k} }$$
の成分を時間$${ t }$$に関して$${ t_0 }$$から$${ t }$$まで定積分することで、その時間区間における位置の変化量を得ます。
位置ベクトルの計算:
位置ベクトルの各成分$${ x(t), y(t), z(t) }$$は、次のように定積分によって求められます。
$$
\int_{t_0}^{t} \bm v(\tau)d\tau=\bm r(t)- \bm r(t_0)
$$
$$
\int_{t_0}^{t} v_x(\tau)d\tau=x(t)- x(t_0)\\
\int_{t_0}^{t} v_y(\tau)d\tau=y(t)- y(t_0)\\
\int_{t_0}^{t} v_z(\tau)d\tau=z(t)- z(t_0)\\
$$
$$
x(t) = x(t_0) + \int_{t_0}^{t} v_x(\tau)d\tau\\
y(t) = y(t_0) + \int_{t_0}^{t} v_y(\tau)d\tau\\
z(t) = z(t_0) + \int_{t_0}^{t} v_z(\tau)d\tau
$$
ここで、$${ \tau }$$は積分変数であり、$${ t_0 }$$は初期時刻、$${ t }$$は終了時刻です。初期位置$${ \bm{r}(t_0) = (x(t_0), y(t_0), z(t_0)) }$$は、積分による変位の基点となります。
例:
物体が時刻$${ t_0 }$$で$${ \bm{r}(t_0) = (0, 0, 0) }$$にあり、速度ベクトルが
$${ \bm{v}(t) = t\bm{i} + 2t\bm{j} + 3t\bm{k} }$$
で与えられている場合、時刻$${ t }$$における位置は次のように計算されます。
$$
x(t) = \int_{t_0}^{t} \tau d\tau = \frac{t^2}{2} - \frac{t_0^2}{2}\\
y(t) = \int_{t_0}^{t} 2\tau d\tau = t^2 - t_0^2\\
z(t) = \int_{t_0}^{t} 3\tau d\tau = \frac{3t^2}{2} - \frac{3t_0^2}{2}
$$
この方法により、初期位置と速度ベクトルが与えられた場合に、任意の時刻における物体の位置を正確に求めることができます。
勾配と速度ベクトル、および速度ベクトル場(多変数入力スカラー値関数の微分)
勾配は多変数入力実数出力の実数値関数であるスカラー場にかかる。勾配の対象となる$${f}$$は$${f(x,y)}$$なり$${f(x,y,z)}$$である。
$${f}$$に勾配を引っ掛けた結果の出力は偏微分のベクトルである。
$$
\nabla f = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z} \right)
$$
また、$${\nabla f}$$は関数$${f}$$の最大傾斜方向を向くベクトル、および等高線の法線となる。
例えば$${z=f(x,y)}$$ならば$${\nabla f=(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y})}$$は各々のzのレベルの等高線に対する法線である。
$${w=f(x,y,z)}$$ならば等値面に垂直なベクトルを指す。等値面とは例えば、空間中の温度に応じて色を塗った場合、同じ色の部分。
他との比較①
多変数入力のスカラー出力の関数に掛かる勾配に対して、
速度ベクトルは時間依存ベクトル値関数$${ \bm r'(t)}$$を微分した結果である。つまり対象となる$${f}$$は1変数$${f(t)}$$であって、この関数の出力はベクトルである。
流体でいうところのラグランジュ式である(物体あるいは粒子等が主体)。
$$
\bm v = \bm r'(t)=\frac{d\bm r}{dt}=(\frac{dx}{dt},\frac{dy}{dt},\frac{dz}{dt})
$$
$$
\bm v = \frac{d\bm r}{dt} = \bm r'(t)=\frac{d\bm r(t)}{dt}=\frac{dx(t)}{dt}\bm i+\frac{dy(t)}{dt}\bm j+\frac{dz(t)}{dt}\bm k
$$
他との比較②
多変数入力のスカラー出力の関数に掛かる勾配に対して、
速度ベクトル『場』の場合、$${f}$$が多変数であって、偏微分を考慮する必要に駆られる。かつ$${f}$$の出力はベクトル。
流体でいうところのオイラー式(物体あるいは粒子等を客観的に観察する)
$$
\bm v(x, y, z) = v_x(x, y, z) \bm{i} + v_y(x, y, z) \bm{j} + v_z(x, y, z) \bm{k}
$$
微分はヤコビアン、微分相当操作はDiv(発散)とCurl(回転)である。勾配は適用できない。
$$
\text{div} \bm{v} = \nabla \cdot \bm{v} = \frac{\partial v_x}{\partial x} + \frac{\partial v_y}{\partial y} + \frac{\partial v_z}{\partial z}
$$
$$
\text{curl} \bm{v} = \nabla \times \bm{v} = \left( \frac{\partial v_z}{\partial y} - \frac{\partial v_y}{\partial z} \right) \hat{i} + \left( \frac{\partial v_x}{\partial z} - \frac{\partial v_z}{\partial x} \right) \hat{j} + \left( \frac{\partial v_y}{\partial x} - \frac{\partial v_x}{\partial y} \right) \hat{k} ]
$$
ナブラは微分演算子であり、成分に微分演算を持つ。
$$
\nabla = (\frac{\partial}{\partial x}, \frac{\partial}{\partial y}, \frac{\partial}{\partial z})
$$
方向微分
方向微分は、多変数関数のある点における特定の方向への微分です。これは、関数がその方向に沿ってどのように変化するかを測定するもので、特に多変数微分積分学において重要な概念です。
方向微分の定義
関数 $${ f(x, y) }$$ について考えると、点 $${ (x_0, y_0) }$$ における単位ベクトル $${ \mathbf{u} = (u_1, u_2) }$$ 方向の方向微分は、以下のように定義されます。
$$
D_{\mathbf{u}} f(x_0, y_0) = \lim_{h \to 0} \frac{f(x_0 + hu_1, y_0 + hu_2) - f(x_0, y_0)}{h}
$$
あるいはベクトル$${\mathbf a}$$を用いて
$$
D_{\mathbf{u}}f(\mathbf{a}) = \lim_{h \to 0} \frac{f(\mathbf{a} + h\mathbf{u}) - f(\mathbf{a})}{h}
$$
ここで$${D_{\mathbf{u}}f}$$は関数名みたいなものであって$${g(\mathbf{a}) = \lim_{h \to 0} \frac{f(\mathbf{a} + h\mathbf{u}) - f(\mathbf{a})}{h}}$$でも良いものですが、やってることは微分なのでDが付くし、範囲を限定しているので$${_u}$$が付きます。なので$${D_{\mathbf{u}}f}$$です。
$${ h }$$ はスカラーで、$${ \mathbf{u} }$$ は $${ \mathbf a(x_0, y_0) }$$ から出る方向を指し示す単位ベクトルです。この限界操作によって連続性が担保され、$${ \mathbf{u} }$$ の方向における関数の局所的な変化率を求めます。
$${\mathbf a}$$は空間の1点を指定した、関数の局所的な振る舞いを見るもので、$${f(\mathbf x)}$$で成り立つことは$${\mathbf a}$$でも成り立つけれど、$${\mathbf a}$$で成り立つからと言って$${f(\mathbf x)}$$で成り立つとは限らないという違いがあります。
方向微分の計算
関数 $${ f }$$ の勾配 $${ \nabla f }$$ が存在する場合、方向微分は次のように簡単に計算できます。
$$
D_{\mathbf{u}} f(x_0, y_0) = \nabla f(x_0, y_0) \cdot \mathbf{u}
$$
$$
D_{\mathbf{u}} f(\mathbf a) = \nabla f(\mathbf a) \cdot \mathbf{u}
$$
ここで、$${ \cdot }$$ はドット積(内積)を示し、$${ \nabla f(x_0, y_0) }$$ は $${ f }$$ の勾配ベクトルで、$${ \mathbf a(x_0, y_0) }$$ における $${ f }$$ の最大増加方向を表します。$${ \mathbf{u} }$$ は方向ベクトルです。
導出
勾配ベクトルの定義
関数 $${ f: \mathbb{R}^n \to \mathbb{R} }$$ が点 $${ \mathbf{a} }$$ で微分可能であるとき、その点での勾配ベクトル $${ \nabla f(\mathbf{a}) }$$ は、各座標方向の偏微分係数を成分とするベクトルとして定義されます:
$$
\nabla f(\mathbf{a}) = \left( \frac{\partial f}{\partial x_1}(\mathbf{a}), \frac{\partial f}{\partial x_2}(\mathbf{a}), \ldots, \frac{\partial f}{\partial x_n}(\mathbf{a}) \right)
$$
テイラー展開の第一項
点 $${ \mathbf{a} }$$ の近傍で $${ f }$$ をテイラー展開の第一項で近似すると、小さな変位 $${ \mathbf{h} }$$ に対して以下のようになります:
$$
f(\mathbf{a} + \mathbf{h}) \approx f(\mathbf{a}) + \nabla f(\mathbf{a}) \cdot \mathbf{h} + o(|\mathbf{h}|)
$$
ここで、$${ o(|\mathbf{h}|) }$$ は $${ \mathbf{h} }$$ が 0 に近づくにつれて $${ |\mathbf{h}| }$$ よりも早く 0 に近づく項です。n次の項は1次の項よりもn乗早く0に近づきます。
方向微分の導出
方向微分はベクトル $${ \mathbf{u} }$$ の方向での関数 $${ f }$$ の微分です。小さなスカラー $${ h }$$ に対して $${ \mathbf{h} = h\mathbf{u} }$$ と置くと、以下のように表せます:
$$
f(\mathbf{a} + h\mathbf{u}) \approx f(\mathbf{a}) + \nabla f(\mathbf{a}) \cdot (h\mathbf{u}) + o(h)
$$
この式から $${ f(\mathbf{a}) }$$ を引いて
$$
f(\mathbf{a} + h\mathbf{u}) - f(\mathbf{a}) \approx \nabla f(\mathbf{a}) \cdot (h\mathbf{u}) + o(h)
$$
$${ h }$$ で割り、
$$
\frac{f(\mathbf{a} + h\mathbf{u}) - f(\mathbf{a})}{h} \approx (\frac{\nabla f(\mathbf{a}) \cdot (h\mathbf{u}) + o(h) }{h}=
\nabla f(\mathbf{a}) \cdot \mathbf{u} + \frac{o(h) }{h})
$$
$${ h }$$ を 0 に近づける極限を取ると、
$$
\lim_{h \to 0} \frac{f(\mathbf{a} + h \mathbf{u}) - f(\mathbf{a})}{h} = \nabla f(\mathbf{a}) \cdot \mathbf{u}
$$
結果、方向微分 $${ D_{\mathbf{u}} f(\mathbf{a}) }$$ は次のように計算できます:
$$
D_{\mathbf{v}} f(\mathbf{a}) = \lim_{h \to 0} \frac{f(\mathbf{a} + h \mathbf{u}) - f(\mathbf{a})}{h} = \nabla f(\mathbf{a}) \cdot \mathbf{u}
$$
この式において、$${ \nabla f(\mathbf{a}) \cdot \mathbf{v} }$$ は、勾配ベクトルと方向ベクトルの内積であり、これが関数が $${ \mathbf{a} }$$ で $${ \mathbf{v} }$$ 方向にどれだけ変化するかを示しています。この内積は、ベクトルの各成分の積の和として計算されます。
例題
関数 $${ f(x, y) = x^2 + y^2 }$$ が与えられたとき、点 $${ (1, 1) }$$ における方向 $${ \mathbf{u} = \frac{1}{\sqrt{2}}(1, 1) }$$ での方向微分を計算してみましょう。
勾配を計算します:
$$
\nabla f(x, y) = (2x, 2y)
$$
したがって、点 $${ (1, 1) }$$ での勾配は $${ (2, 2) }$$ です。
方向微分を計算します:
$$
D_{\mathbf{u}} f(1, 1) = (2, 2) \cdot \frac{1}{\sqrt{2}}(1, 1) = \frac{1}{\sqrt{2}}(2 + 2) = 2\sqrt{2}
$$
この結果は、方向 $${ \mathbf{u} }$$ における $${ f }$$ の増加率を示し、この方向が $${ f }$$ が最も速く増加する方向の一つであることを示します。
方向微分と全微分
全微分と方向微分の幾何学的な解釈
全微分は、関数の曲面上の点から別の近くの点への移動に伴う関数値の変化を表しています。一方、方向微分は、関数の曲面上のある点において、特定の方向に少し移動したときの関数値の変化率を表しています。
全微分は全ての変数の微小な変位に応じた関数の変化、
方向微分はある点における、ある方向への微小な変位に応じた関数の変化
単位ベクトルである方向ベクトル$${\mathbf{u} = (u_x, u_y, u_z)}$$に対して
$${f}$$の点$${\mathbf a}$$における局所的な勾配
$$
\nabla f(\mathbf{a}) = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z} \right)
$$
として、
その関数のある方向に対する局所的な増加率である方向微分は
$$
D_{\mathbf u}f(\mathbf a)=\nabla f(\mathbf{a})\cdot \mathbf u = \frac{\partial f}{\partial x} u_x + \frac{\partial f}{\partial y} u_y + \frac{\partial f}{\partial z} u_z
$$
方向微分は勾配ベクトルが$${\mathbf u}$$方向に落とした影の長さ=その方向の関数$${f(\mathbf a)}$$の局所的な増加率
対して全微分は
$$
df = \frac{\partial f}{\partial x} dx + \frac{\partial f}{\partial y} dy + \frac{\partial f}{\partial z} dz
$$
$$
df = \nabla f \cdot \mathbf{dr}
$$
全微分の変位$${\mathbf{dr}}$$を単位ベクトル化すると
$$
\frac{df}{|\mathbf {dr}|} = \nabla f \cdot \frac{\mathbf{dr}}{|\mathbf {dr}|}
$$
ここで$${\mathbf u=\frac{\mathbf{dr}}{|\mathbf {dr}|}}$$ならば
$$
\frac{df}{|\mathbf {dr}|} = D_{\mathbf{u}} f = \nabla f \cdot \mathbf{u} = \frac{\nabla f \cdot \mathbf{dr}}{|\mathbf{dr}|}
$$
方向微分と勾配
関数 $${ f(x, y) }$$ の最大増加方向が勾配 $${ \nabla f }$$ の方向であるという事実は、ベクトル解析における基本的な結果です。これを証明または説明するには、方向微分を用いるのが一般的です。以下にその詳細を説明します。
方向微分は、特定の方向における関数の変化率を測定します。
つまり方向微分が最大値となる方向が、関数 $${ f(x, y) }$$ の最大増加方向です。
点 $${ (x, y) }$$ で関数 $${ f(x, y) }$$ の任意の単位ベクトル $${ \mathbf{u} = (u_1, u_2) }$$に沿った方向微分は、以下の式で定義されます。
$$
D_{\mathbf{u}} f = \nabla f \cdot \mathbf{u}
$$
ここで、$${ \nabla f = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right) }$$ は $${ f }$$ の勾配ベクトルです。
勾配が最大増加方向である理由
ドット積の性質:
ベクトル $${ \mathbf{a} }$$ と $${ \mathbf{b} }$$ のドット積は、$${ \mathbf{a} \cdot \mathbf{b} = |\mathbf{a}| |\mathbf{b}| \cos \theta }$$ で与えられます。ここで $${ \theta }$$ はベクトル間の角度です。
方向微分の最大化: $${ D_{\mathbf{u}} f }$$ を最大化するには、$${ \cos \theta }$$ を最大化する必要があります。$${ \cos \theta }$$ が最大となるのは $${ \theta = 0 }$$(つまり、$${ \mathbf{u} }$$ と $${ \nabla f }$$ が同じ方向)のときで、この値は 1 です。
最大方向微分: よって、$${ D_{\mathbf{u}} f }$$ の最大値は、
$$
\mathbf u = \frac{\nabla f}{|\nabla f|}\\
\nabla f \cdot \frac{\nabla f}{|\nabla f|} = |\nabla f|
$$
となり、これは $${ \mathbf{u} }$$ が $${ \nabla f }$$ と同じ方向のとき、つまり $${ \mathbf{u} }$$ が $${ \nabla f }$$ と平行な単位ベクトルのときに達成されます。
したがって、勾配 $${ \nabla f }$$ の方向は、関数 $${ f(x, y) }$$ の最大増加方向$${\frac{\nabla f}{|\nabla f|}}$$です。これは方向微分が最大になる方向であり、勾配の方向と一致します。この説明は多変数関数の局所的な挙動を理解するのに重要であり、多くの数学的および物理的現象の解析において基本的なツールとなっています。
勾配が法線方向である理由
まず、関数 $${f(x, y)}$$ があるとします。この関数の等高線は $${ f(x, y) = c }$$($${ c }$$ は定数)と表されます。この等高線上の任意の点において、関数の値は変わりません。つまり、その点を通る等高線に沿った方向の変化はゼロです。この方向をベクトル $${ \mathbf{v} }$$ とすると、$${ f }$$ の方向微分 $${ \nabla f \cdot \mathbf{v} }$$ はゼロになります。これは $${ \nabla f }$$(勾配)が $${ \mathbf{v} }$$ に垂直であることを意味します。
他
Q:
ある関数 $${z=f(x,y)}$$ の勾配が $${(2x, -2y)}$$ だった時、$${2x}$$ と $${-2y}$$ は、それぞれ $${x}$$ と $${y}$$ の一次関数であり、三次元空間内で $${z=f(x,y)}$$ のグラフ上の各点において接平面を定義するか。
Claude3
はい、その通りです。ある関数 $${z=f(x,y)}$$ の勾配が $${(2x, -2y)}$$ である場合、$${2x}$$ と $${-2y}$$ はそれぞれ $${x}$$ と $${y}$$ の一次関数であり、これらの一次関数は三次元空間内で $${z=f(x,y)}$$ のグラフ上の各点において接平面を定義します。
具体的には、$${z=f(x,y)}$$ の勾配ベクトル $${\nabla f(x,y) = (2x, -2y)}$$ は、関数のグラフ上の各点 $${(x,y,f(x,y))}$$ において、その点での接平面の法線ベクトルを表しています。
この接平面の方程式は、以下のように表すことができます。
$${z = 2x(x-x_0) - 2y(y-y_0) + f(x_0,y_0)}$$
ここで、$${(x_0,y_0)}$$ は $${z=f(x,y)}$$ 上の任意の点です。
この接平面は、点 $${(x_0,y_0,f(x_0,y_0))}$$ において $${z=f(x,y)}$$ のグラフに接しており、$${2x}$$ と $${-2y}$$ で表される一次関数の組み合わせによって定義されています。
したがって、$${2x}$$ と $${-2y}$$ は、三次元空間内の $${z=f(x,y)}$$ のグラフ上の各点で接平面を定義する一次関数であると言えます。これらの接平面は、多変数関数の局所的な振る舞いを理解するための重要な概念です。
Q:
関数 $${z=f(x,y)}$$ の勾配ベクトル $${\nabla f(x,y) = (2x, -2y)}$$ は、接平面上のベクトルであり、$${z=f(x,y)}$$ の最大増加方向を表すか?
Claude3
はい、その通りです。関数 $${z=f(x,y)}$$ の勾配ベクトル $${\nabla f(x,y) = (2x, -2y)}$$ は、接平面上のベクトルであり、$${z=f(x,y)}$$ の最大増加方向を表します。
勾配ベクトルは、関数のグラフ上の各点において、その点での関数値の変化率が最大となる方向を指しています。言い換えれば、勾配ベクトルは、その点から微小距離だけ移動したときに、関数値が最も急激に増加する方向を表しています。
したがって、$${\nabla f(x,y) = (2x, -2y)}$$ は、$${z=f(x,y)}$$ のグラフ上の各点における接平面上のベクトルであり、その点での関数の最大増加方向を表していると言えます。
実数値関数微分の近似(テイラー展開1次まで)
1変数および多変数の、出力実数の関数の場合は微分がたやすく近似できる。ベクトル値関数とベクトル場にはこのままでは適用できず、もうひと手間かかる。
1変数の場合
$$
f(x+\Delta x)\fallingdotseq\\
f(x)+\Delta f = f(x)+f'(x)\Delta x
$$
$$
\Delta f \fallingdotseq f'(x)\Delta x
$$
これはテイラー展開1次の項まで。
2変数の場合
$$
f(x+\Delta x, y+\Delta y)\fallingdotseq\\
f(x,y)+\Delta f = f(x,y)+f_x(x,y)\Delta x+f_y(x,y)\Delta y=f(x,y)+\frac{\partial f}{\partial x}\Delta x+\frac{\partial f}{\partial y}\Delta y
$$
$$
\Delta f \fallingdotseq\\
f_x(x,y)\Delta x+f_y(x,y)\Delta y=\frac{\partial f}{\partial x}\Delta x+\frac{\partial f}{\partial y}\Delta y
$$
3変数の場合
$$
f(x+\Delta x, y+\Delta y+\Delta z)\fallingdotseq\\
f(x,y,z)+\Delta f = f(x,y,z)+f_x(x,y,z)\Delta x+f_y(x,y,z)\Delta y+f_z(x,y,z)\Delta z=f(x,y,z)+\frac{\partial f}{\partial x}\Delta x+\frac{\partial f}{\partial y}\Delta y+\frac{\partial f}{\partial z}\Delta z
$$
$$
\Delta f\fallingdotseq \\
f_x(x,y,z)\Delta x+f_y(x,y,z)\Delta y+f_z(x,y,z)\Delta=\frac{\partial f}{\partial x}\Delta x+\frac{\partial f}{\partial y}\Delta y+\frac{\partial f}{\partial z}\Delta z
$$
ここで
$$
\nabla f = (\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z})\\
\Delta\bm r=(\Delta x, \Delta y, \Delta z)
$$
とすると
$$
\Delta f=\nabla f\cdot \Delta \bm r
$$
ベクトル入力スカラー出力関数 $${f(\bm r)}$$ の場合:
$$
f(\bm r + \Delta\bm r) \fallingdotseq f(\bm r) + \nabla f(\bm r) \cdot \Delta\bm r
$$
ここで、
$${\bm r = (x_1, x_2, \ldots, x_n)}$$
$${\Delta\bm r = (\Delta x_1, \Delta x_2, \ldots, \Delta x_n)}$$
$${\nabla f(\bm r) = (\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \ldots, \frac{\partial f}{\partial x_n})}$$
です。
ベクトル値関数 $${\bm f(\bm r) = (f_1(\bm r), f_2(\bm r), \ldots, f_m(\bm r))}$$ の場合:
$$
\bm f(\bm r + \Delta\bm r) \fallingdotseq \bm f(\bm r) + J(\bm f(\bm r)) \Delta\bm r
$$
ここで、$${J(\bm f(\bm r))}$$ はヤコビ行列であり、以下のように定義されます。
$$
J(\bm f(\bm r)) =
\begin{pmatrix}
\frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} & \cdots & \frac{\partial f_1}{\partial x_n} \\
\frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} & \cdots & \frac{\partial f_2}{\partial x_n} \\
\vdots & \vdots & \ddots & \vdots \\
\frac{\partial f_m}{\partial x_1} & \frac{\partial f_m}{\partial x_2} & \cdots & \frac{\partial f_m}{\partial x_n}
\end{pmatrix}
$$
ベクトル場 $${\bm F(\bm r) = (F_1(\bm r), F_2(\bm r), \ldots, F_n(\bm r))}$$ の場合:
$$
\bm F(\bm r + \Delta\bm r) \fallingdotseq \bm F(\bm r) + J(\bm F(\bm r)) \Delta\bm r
$$
ここで、$${J(\bm F(\bm r))}$$ はヤコビ行列であり、以下のように定義されます。
$$
J(\bm F(\bm r)) =
\begin{pmatrix}
\frac{\partial F_1}{\partial x_1} & \frac{\partial F_1}{\partial x_2} & \cdots & \frac{\partial F_1}{\partial x_n} \\
\frac{\partial F_2}{\partial x_1} & \frac{\partial F_2}{\partial x_2} & \cdots & \frac{\partial F_2}{\partial x_n} \\
\vdots & \vdots & \ddots & \vdots \\
\frac{\partial F_n}{\partial x_1} & \frac{\partial F_n}{\partial x_2} & \cdots & \frac{\partial F_n}{\partial x_n}
\end{pmatrix}
$$
これらの式は、それぞれの関数やベクトル場の微小変化を、勾配ベクトルやヤコビ行列を用いて一次近似しています。
弧長
$$
s=\int_a^b{|\frac{d\bold r}{dt}|}dt=\int_a^b|\bold r'(t)|dt
$$
位置ベクトルの経路の長さ。曲線の長さ。
弧長に対して具体的な数値を当てはめるのは意外とめんどくさい。(結局曲線全体の弧長を求めて弧長/全体弧長=tみたいになると思われるが、じゃあその全体の弧長がちゃんとでるかという話になると思われる。そのためにはx(t),y(t)が全部既知で、$${\bold r(x(t),y(t))}$$も全部分かってるとなるとじゃあなにが分からんのだという話になると思われる)が、弧長sをr(s)のように位置関数(ベクトル関数)のパラメータととると、接線ベクトルが単位ベクトルになるという謎の便利性質の所為で気軽に導入される。
tで微分すると接線ベクトルは都度長さが変わるが、sで微分すると全部同じ、というかこの場合は長さ1の単位ベクトルになるということである。
$$
\left|\frac{d\bold r}{ds}\right| = 1
$$
なんでか
弧長 $${s}$$ が曲線に沿った距離を表すことから、$${s}$$ の単位変化に対する位置ベクトルの変化量が常に1になる理由を説明します。
まず、弧長 $${s}$$ の定義を思い出してください。
$$
s=\int_a^b{|\frac{d\bold r}{dt}|}dt=\int_a^b|\bold r'(t)|dt
$$
ここで、$${t}$$ を $${s}$$ の関数として考えます。つまり、$${t=t(s)}$$ とします。これは、弧長 $${s}$$ が $${t}$$ の関数として表されることを意味します。
次に、合成関数の微分則を使って、$${\frac{d\bold r}{ds}}$$ を計算します。
$$
\frac{d\bold r}{ds} = \frac{d\bold r}{dt} \cdot \frac{dt}{ds}
$$
ここで、$${\frac{dt}{ds}}$$ は $${s}$$ の関数としての $${t}$$ の微分です。この値を求めるために、弧長の定義式を $${s}$$ で微分します。
$$
1 = \frac{ds}{ds} = \left|\frac{d\bold r}{dt}\right| \cdot \frac{dt}{ds}
$$
よって、
$$
\frac{dt}{ds} = \frac{1}{\left|\frac{d\bold r}{dt}\right|}
$$
これを $${\frac{d\bold r}{ds}}$$ の式に代入すると、
$$
\frac{d\bold r}{ds} = \frac{d\bold r}{dt} \cdot \frac{1}{\left|\frac{d\bold r}{dt}\right|} = \frac{\frac{d\bold r}{dt}}{\left|\frac{d\bold r}{dt}\right|}
$$
右辺は、$${\frac{d\bold r}{dt}}$$ を正規化したベクトル(単位ベクトル)です。したがって、
$$
\left|\frac{d\bold r}{ds}\right| = 1
$$
が成り立ちます。
つまり、弧長 $s$ で微分した接線ベクトル $${\frac{d\bold r}{ds}}$$ は、常に長さが1の単位ベクトルになります。これは、弧長 $${s}$$ が曲線に沿った距離を表すためです。$${s}$$ の単位変化は、曲線上の単位長さの変化に対応し、それに伴う位置ベクトルの変化量は常に1になるのです。
いろんなことを削ぎ取ってプログラムにした場合、区間の長さ全部足すとしか言ってない。以下の例の場合、
弧長s_iはindex[i]の時のsumである。
線素はlv.lengthである。
double ArcLength(List<Vector2D> arc)
{
double sum;
for(int i = 0; i<arc.Length-1; i++)
{
var sv = arc[i];
var ev = arc[i+1];
var lv = ev-sv;
sum+=lv.Length;
}
}線素
$${ds}$$のこと
微小な弧長の差。曲線の長さの差。差なので大きさ。スカラー。
弧長の微小な変位。弧長がsなら線素はds
また、位置ベクトル$${\bold r}$$の微小な変位を示す変位ベクトルの大きさds。
$${ds=|d\bold s|=|d\bold r|=|\bold t ds|}$$
線素を最も単純に考えるなら、前述lv.lengthはすべて同じ長さと考える。これは$${\Delta s}$$が定数ならばという話で、$${\Delta s}$$が関数ならば話は別である。例えば$${ds=\sqrt{dx^2+dy^2}}$$とみて、ds,dx,dyがtなりなんなりのパラメータをとる関数ならば同じ長さとは限らない。
最も単純に、曲線全体を同じ大きさの線素で分割した時、分割された同じ大きさのベクトルを線素ベクトルという。ゆえに線素ベクトルを線素で割ると単位ベクトルであり($${\frac{d \bold s}{ds}=\bold t}$$)、それが$${d \bold r=d \bold s}$$ならば$${\frac{d}{ds}\bold r=\bold t}$$になる。
曲線全体を適当な大きさ(線素の関数)で分割した時、分割された適当な大きさのベクトルが線素ベクトルとなり、線素との対によって単位ベクトルとなる$${\frac{d\bold s(t)}{ds(t)}=\bold t}$$。
線素ベクトル
$${d\bold s=d \bold r}$$のこと
位置ベクトルrの微小な変位ベクトル
線素ベクトルの大きさは線素である。
tを変位方向の単位ベクトル(単位接線ベクトル)とすると
$${\bold t}$$は
$${|\bold t|=1}$$
$${\bold t=\frac{\bm r'(t)}{|\bm r'(t)|}=\frac{\bold r_2-\bold r_1}{|\bold r_2-\bold r_1|}}$$
位置$${\bold r}$$は弧長で微分すると単位ベクトルとなる
これは位置、あるいは曲線をr(s(t))ととった時の単位弧長あたりの位置の変位。
$$
\bold t = \frac{d\bold r}{ds}
$$
あるいは、なんならここから定義しても良いと思われるが
線素ベクトルをその大きさ(線素)で割ったら単位ベクトル
$$
\bold t = \frac{d\bold s}{ds}
$$
線素ベクトル$${d\bold s=d \bold r}$$は
$$
d\bold s=d\bold r=\bold t ds\\
d\bold r = \frac{\bold r_2 - \bold r_1}{||\bold r_2 - \bold r_1||}ds
$$
曲線のパラメータ$${t}$$の微小な変化$${dt}$$で除する(位置ベクトル$${\bold r}$$を$${t}$$で微分する)場合、それは単なる接線ベクトルである。
$$
\frac{d\bold s}{dt}=\frac{d\bold r}{dt}=\frac{\bold t ds}{dt}=(\frac{dx(t)}{dt},\frac{dy(t)}{dt},\frac{dz(t)}{dt})
$$
$${d\bold r}$$単品の方が微小感があり、
$${\frac{d\bold r}{dt}}$$はパラメータ$${t}$$に応じてる感がある。
しぬ程雑な例。x(t)=3t,y(t)=4tとかの時。
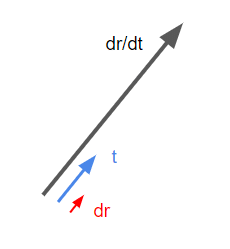
パラメータtに応じる線素ds
$$
d\bm r\\
\bm v =\frac{d\bm r}{dt}\\
\bm a =\frac{d\bm v}{dt}\\
$$
$$
ds = |d\bm r|\\
v =|\bm v|\\
$$
$$
v=\frac{ds}{dt}\\
ds= vdt
$$
二次元空間における位置ベクトル$${\bm r}$$の変位ベクトル$${d\bm r}$$は
$$
d\bm r=(dx, dy)
$$
その大きさは微小距離のピタゴラス
$$
|d\bm r| = ds = \sqrt{dx^2 + dy^2}
$$
位置ベクトルの単位時間当たりの変位はすなわち速度ベクトル
$$
\bm v=\frac{d\bm r}{dt}=(\frac{dx}{dt}, \frac{dy}{dt})\\
\bm v(t)=\frac{d\bm r(t)}{dt}=(\frac{dx(t)}{dt}, \frac{dy(t)}{dt})\\
$$
その大きさは速度
$$
|\bm v|=v=\sqrt{(\frac{dx}{dt})^2 + (\frac{dy}{dt})^2}=\sqrt{(\frac{dx(t)}{dt})^2 + (\frac{dy(t)}{dt})^2}=\sqrt{\left(\frac{d}{dt}x(t)\right)^2 + \left(\frac{d}{dt}y(t)\right)^2}
$$
$${ds=vdt}$$から
$$
|d\bm r|= ds =\sqrt{(\frac{dx}{dt})^2 + (\frac{dy}{dt})^2}dt=\sqrt{\frac{(dx)^2+(dy)^2}{(dt)^2}}dt=\frac{\sqrt{(dx)^2+(dy})^2}{\sqrt{(dt)^2}}dt=\frac{\sqrt{(dx)^2+(dy})^2}{dt}dt=
\sqrt{(dx)^2 + (dy)^2}
$$
3次なら
$$
|d\mathbf{r}| = ds = \sqrt{dx^2 + dy^2 + dz^2} = \sqrt{\left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2 + \left(\frac{dz}{dt}\right)^2} dt
$$
弧長sの微分=速度
dsをdtで割ると単位tあたりの弧長、
弧長sの時間あたりの変化の割合、
時間当たりの位置ベクトルの変位の大きさ、
接線ベクトルの大きさ、速度。
$$
\left| \frac{d\mathbf{r}}{dt} \right| =|\bm v|=v = \frac{ds}{dt} = \sqrt{\left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2 + \left(\frac{dz}{dt}\right)^2} \qquad
$$
面積要素、面素
面素ベクトルの大きさdS
$$
dS = \left| \frac{\partial \mathbf{r}}{\partial u} \times \frac{\partial \mathbf{r}}{\partial v} \right| du dv \qquad
$$
面素ベクトル
$$
d\mathbf{S} = d\mathbf{r}_1 \times d\mathbf{r}_2 \qquad
$$
$${\bm n}$$を法線とすると
$$
d\bm S=\bm ndS
$$
体積要素
$$
dV=d\bm r_1 \cdot (d\bm r_2 \times d \bm r_3)
$$
法線
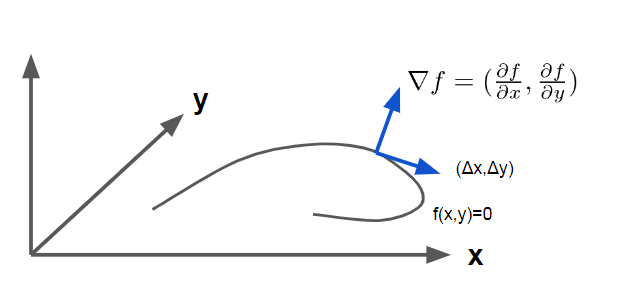
位置ベクトル$${\bm r(t)}$$の場合、微分するだけで接ベクトル=速度ベクトルがとれたが、実数値多変数関数$${f(x,y)}$$の場合は同じようにはいかない。ただし$${f(x,y)}$$の場合は勾配をとるだけで法線が得られる。
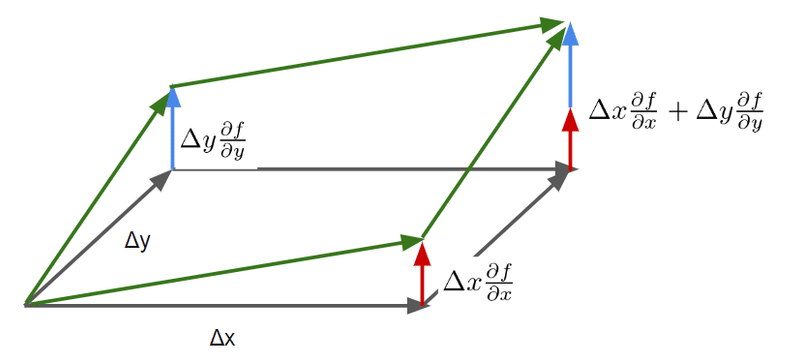
$${\Delta x, \Delta y}$$が曲線$${f(x,y)=0}$$の進行方向。
$${(\Delta x, \Delta y)=(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y})}$$ならば$${f(x,y)}$$の出力値は最も変化する。
逆に言えば$${\nabla f = (\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y})}$$と直交する方に進行すれば$${f(x,y)}$$は変化しない。これは例えば曲線$${f(x,y)=0}$$上を移動するとそうなる。
陽関数z=f(x,y)の場合
その勾配ベクトル
$$
\nabla f = (\frac{\partial f}{\partial x},\frac{\partial f}{\partial y})
$$
は、$${z}$$の変位($${\Delta z}$$)が最大となる方向を向くベクトルとなる。このベクトルは等位曲線(高等線)に対して垂直、法線となる。
この法線は単位ベクトルとは限らない。
等位曲線(高等線)
ある関数$${f(x,y)}$$において、出力が
$${f(x,y)=\text{定数}}$$
を満たす$${(x,y)}$$の組全部がなす曲線。
例えば
$${z=f(x,y)}$$において
$${z=1, 2, 3,…}$$
とし、それを満たす$${(x,y)}$$を適切にプロットすれば等高線となる。
それらの高等線は$${f(x,y)-z=0}$$であって$${g(x,y,f(x,y))=0}$$ないし新たな陰関数$${g(x,y,z)=f(x,y)-z=0}$$をなす。
今$${z=0}$$、すなわち$${f(x,y)=0}$$を考える。
関数$${f()}$$は適当に$${2x+2y}$$とすると$${f(x,y)=2x+2y=0}$$
これは$${g(x,y,z)}$$で表しても$${g(x,y,0)=f(x,y)-z=0}$$である。
$${g(x,y,0)}$$の勾配ベクトル(法線)は$${(2,2,0)}$$。
XY平面上の原点$${(x,y)=(0,0)}$$において、その点からみたZ軸上の座標ベクトルは$${(0,0,z)}$$であって、今はたまたま$${z=0}$$であるとみているが、そうでなくとも$${z}$$が定数であるならば、勾配とった時の成分は$${0}$$。勾配ベクトルとZ軸上の座標ベクトルは内積すると常に$${0}$$、直交している。
$$
\text{Z軸上において}\\
\nabla g(x,y,z) \cdot \bm r(x,y,z)=0
$$
これはつまり法線はZ軸に直交していると言っているに過ぎない。
$${z=f(x,y)}$$を
$${g(x,y,f(x,y))=0}$$ ないし $${g(x,y,z)=0}$$
とした場合、
$${z}$$は$${f(x,y)}$$を切断する走査線の位置を決めているにすぎない
つまりより一般的な陰関数$${h(x,y,z)=0}$$と
$${z=f(x,y)}$$から構築された等位曲線${{g(x,y,f(x,y))}$$は微妙に挙動が異なる。
後述接平面と合わせた理解が必要。
陰関数曲面f(x,y,z)=0の場合
より一般的なf(x,y,z)=0の場合
勾配ベクトルは接平面に対して法線となる。スカラー場の偏導関数の組。
$$
\bm n = \nabla f = (\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z})
$$
この法線は単位ベクトルとは限らない。
$${z=f(x,y)}$$の勾配ベクトルは等位曲線の法線であり、
$${f(x,y,z)=0}$$の勾配ベクトルは接平面の法線である。
その差は
$${z=f(x,y)}$$を変形して$${f(x,y)-z=0}$$
すなわち$${g(x,y,f(x,y))=0}$$を構築できることによる。
$${z=f(x,y)}$$の勾配ベクトルは、$${g(x,y,f(x,y))=0}$$から見れば接平面の法線でもある。
接平面
そもそも平面とは
そもそも平面は
法線と、それに直交するベクトル全部で表される。
平面の方程式は
$${ax+by+cz+d=0}$$
ないし
原点と2つのベクトルをもって
$${\bm u = s\bm v+t\bm w}$$
あるいは
$$
a(x-x_0)+b(y-y_0)+c(z-z_0)=0
$$
ここで(a,b,c)は法線であり、括弧の中は座標とその変位と見ることができる。
一般化すると超平面となり
$$
\mathbf w \cdot \mathbf x + b=\sum\limits_i w_ix_i + b= 0
$$
ここでbは切片ないしバイアスであり、b=0なら超平面は原点を中心にくるくる回る。また、bにより法線方向に平行移動する。
z=f(x,y)の場合
接平面は$${f_x=\frac{\partial f}{\partial x}, f_y=\frac{\partial f}{\partial y}}$$として、
$$
z=f_x(x-x_0)+f_y(y-y_0)+z_0
$$
であり、$${f_x(x-x_0)+f_y(y-y_0)+(z-z_0)=0}$$であるから
$$
\frac{\partial f}{\partial x}\Delta x+\frac{\partial f}{\partial y}\Delta y+\Delta z=0
$$
であって
$$
(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, 1)\cdot (\Delta x, \Delta y, \Delta z)=0
$$
である。
また$${f(x,y)=z_0}$$とみれば
$$
z=f(x,y)+\frac{\partial f}{\partial x}\Delta x+\frac{\partial f}{\partial y}\Delta y
$$
であって、これはテイラー展開の1次近似である。
1次近似は直線をあてはめる。$${y=f(x)+\frac{df}{dx}\Delta x}$$
1次元の関数(曲線)上のある点に対して直線を対応させるならそれは接線。線形補間の2次元版は、曲面上のある点に対して平面を対応させることになる。
ここで
$$
z-f(x,y)=\frac{\partial f}{\partial x}\Delta x+\frac{\partial f}{\partial y}\Delta y
$$
として$${z-f(x,y)}$$を$${\Delta f}$$($${=\Delta z}$$)とするとき、$${\Delta f=0}$$を満たすのが接平面。
$$
\Delta f=\frac{\partial f}{\partial x}\Delta x+\frac{\partial f}{\partial y}\Delta y=0
$$
$$
\Delta f =\nabla f \cdot \Delta \bm r=0
$$
ここで$${\Delta}$$はラプラシアンでなく変位を意味する。
$${\nabla f}$$は法線、あるいは勾配ベクトル
位置ベクトルの変位と法線(勾配ベクトル)の内積とって0を満たす点は接平面。
平面の方程式との違いは
f(x,y,z)=0かg(x,y,f(x,y))=0かである。
z=f(x,y)ないしg(x,y,f(x,y))=0の法線とは、
g(x,y,f(x,y))=0の接平面に対する法線であるが、
より一般的なf(x,y,z)=0と違ってz単体に応じた変化をしないため、
その法線のz成分は常に1
(例えば関数f(x,y)=2x+2yをxで微分すると2、yで微分すると2、zで微分するとf(x,y)=2x+2y=zだからzをzで微分して1)
等位曲線視点で見ると変位(dx,dy)ベクトルに対して直交というか垂直というか、より2次元的には直角な方向を常に指す。
ゆえにz=f(x,y)の勾配ベクトルは等位曲線の法線となる。
同時にg(x,y,f(x,y))形の接平面の法線でもある。
f(x,y,z)=0の場合
$$
df=\nabla f \cdot d\bm r = 0
$$
例えば3次なら
$$
df=\frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial y}dy+\frac{\partial f}{\partial z}dz=0
$$
あるいは
$$
\Delta f=\frac{\partial f}{\partial x}\Delta x+\frac{\partial f}{\partial y}\Delta y+\frac{\partial f}{\partial z}\Delta z=0
$$
全微分
3変数スカラー値関数、スカラー場f(x,y,z)の場合
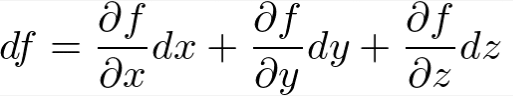
接平面は
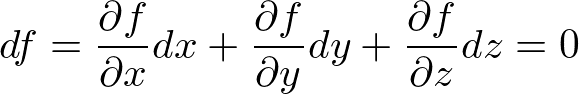
を成す全ての点(x,y,z)で与えられる。
これは勾配ベクトルと、位置ベクトルの微小変位(ベクトル)が内積0で直交するということ。
以下のような外積の結果を基底みたいにとるようなやつみたいなのを微分形式という。以下は一次の微分形式。
$$
M(x,y)dx+N(x,y)dy=0
$$
この時
$$
\frac{\partial F}{dx}=M(x,y)\\\frac{\partial F}{dy}=N(x,y)
$$
なる関数Fが存在すれば
$$
dF=\frac{\partial F}{dx}dx+\frac{\partial F}{dy}dy=0
$$
この形を完全微分形という。
ナブラ(ハミルトン演算子)
スカラー場に作用したりベクトル場に作用したりする。
スカラー場に作用すると勾配grad
ベクトル場との内積をとると発散div
いつものそのへんで良く見るベクトルは要素に値をとる組であるが、ナブラは要素に演算をとる組。ベクトルという言葉がただの要素の組であることを意味するなら、やはりナブラもベクトル。
プログラミング的に言うなら、要素に値をとる配列か、要素に関数をとる配列かの違いになる。
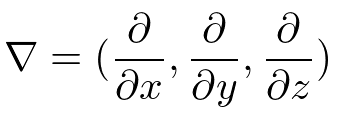
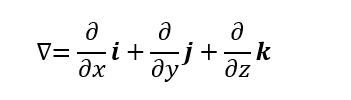
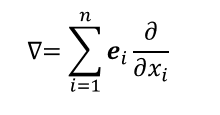
勾配
スカラー場の勾配(grad)はベクトル場。勾配=スカラー場にナブラを作用させたもの。出力はベクトル。
fはf(x,y)とかf(x,y,z)とか
ベクトルに係数を掛けるとベクトルの要素が各々係数倍されるが、演算の組であるナブラにやはり演算であるスカラー場を引っ掛けると、ナブラの各々の要素にスカラー場が分配される。
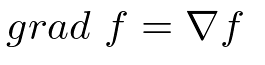
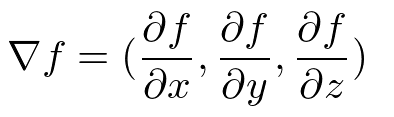
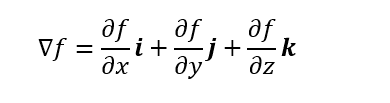
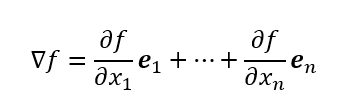
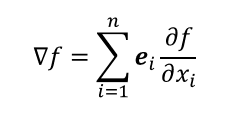
でき上がった勾配はそれ自体、引数にスカラー(x,y,z)を受け、ベクトルを出力する関数である。ベクトル場である。演算と演算の分配は新しい演算をつくる。
また、
あるスカラー場の勾配をとることは、スカラー場をベクトルで微分したとみることもできる。
$$
\bm w=(x,y,z)
$$
の時
$$
\nabla f=\frac{\partial f}{\partial \bm w} =(\frac{\partial f}{\partial x} ,\frac{\partial f}{\partial y} ,\frac{\partial f}{\partial z} )
$$
発散
ベクトル場の発散divはスカラー吐くスカラー場。発散=ベクトル場とナブラの内積をとったもの。出力はスカラー。
F(f,g,h)はF(f(x,y),g(x,y),h(x,y))なりF(f(x,y,z),g(x,y,z),h(x,y,z))
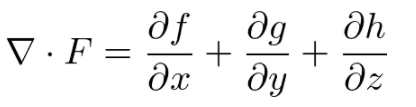
内積はベクトルの要素ごとの積の総和。
この場合、要素に演算をとるベクトル同士の積の和ということになる。
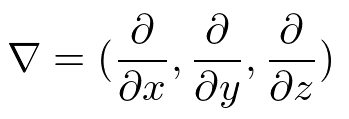
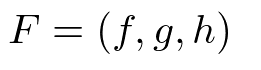
これは入力に関数をとるベクトル場と、入力にスカラー(x,y,z)をとるベクトル場の内積である。結果できあがるのは入力にスカラー(x,y,z)をとり、ベクトルを出力する関数、ベクトル場である。
勾配はベクトル場なので発散に引っ掛けることができる。そうすると下のラプラシアン。
ラプラシアン
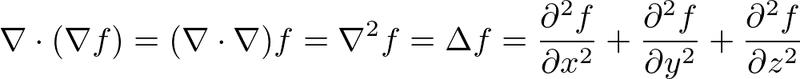
回転
ベクトル場の回転rotはベクトル吐くベクトル場。回転=ベクトル場とナブラの外積をとったもの。出力ベクトル。出力ベクトルが大きい方が小さいやつよりくるくる回っとると考える。
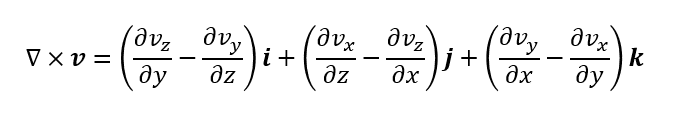
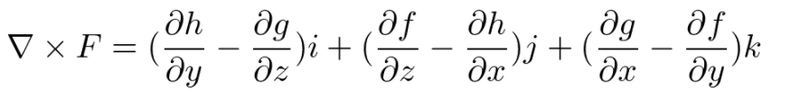
外積は成分間のズレ。釣り合ってれば動かないし、ずれてれば動く。どこかを中心にして動くのならそれは回る。
スカラー場の線積分
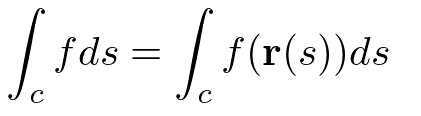
閉曲線の場合は周回積分
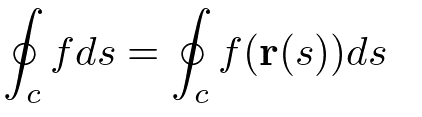
tの場合
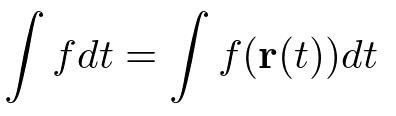
sからt
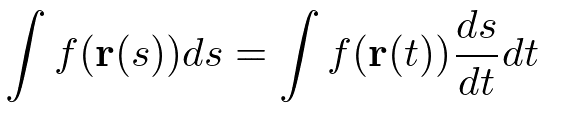
ベクトル場の線積分
ベクトル場と微小ベクトルの内積の総和となる。
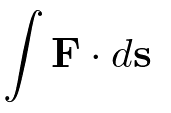
線素ベクトルは曲線上にびっしりと生えていることが予想されるから、それら分だけ内積をとり、総和をとる。
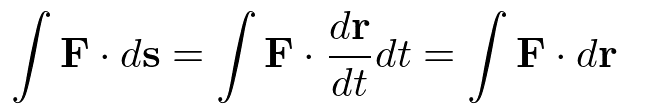
スカラー場の面積分
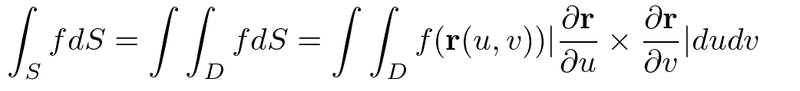
インテグラルのSは面、Dはu,vの領域。dSは面素。dSは面素ベクトル。
ベクトル場の面積分
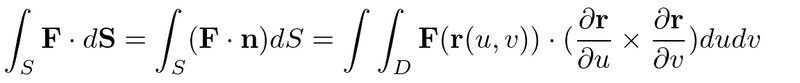
ガウスの勾配定理
$${\Omega}$$を領域全体、$${\Gamma}$$を境界、領域全体に及ぶスカラー場を$${f}$$とすると
$$
\int_\Omega \nabla f \,dV = \int_\Gamma\, f \bold n \, dS
$$
領域が体積なら境界は面
領域が面なら境界は線
領域が線なら境界は点
ガウスの発散定理
体積分と面積分がくっつく。
ある3次元領域の単位体積当たりの発散(=湧き出し・吸い込み)を全部足すと、3次元領域の境界となる表面から出たり入ったりした量に一致する。
右辺は単位面積当たりが担うベクトル場Aの成分を全部足したもの。nは微小面の単位法線であり、長さ1の単位ベクトルとの内積は、あるベクトルがその単位ベクトル方向に落とす射影であり、あるベクトルから単位ベクトル方向に掛かっている成分である。
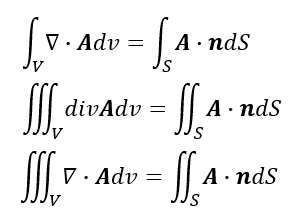
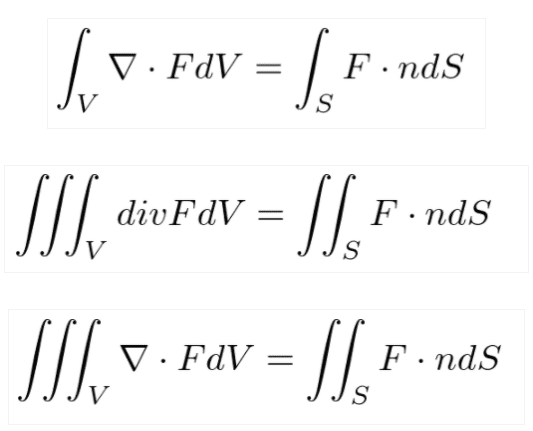
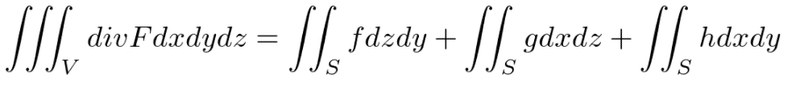
右辺に関して
あるベクトルと単位ベクトルとの内積は、あるベクトルが単位ベクトル方向に落とす射影の大きさ。内積なので出力はスカラー。
内積は
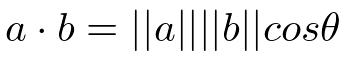
片方が単位ベクトルだと
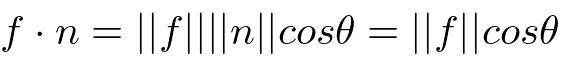
この、水なり気体なりのなにがしかの量が微小面から湧き出すと考えると、その流量は
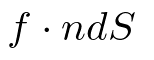
閉曲面全体、表面全体に関して湧き出し量を求めると右辺、面積分。
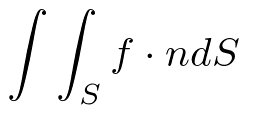
いつもの積分は1つの変数の変化に伴う関数値f(x)の総和。面積分は2つの変数の変化に伴う関数値f(x,y)の総和。体積分は3つの変数に伴う関数値f(x,y,z)の総和。
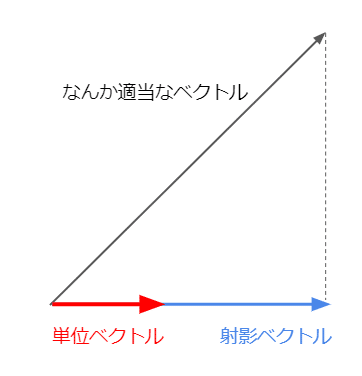
ストークスの定理
曲面Sの面積分と、その境界の閉曲線Cの線積分がくっつく。
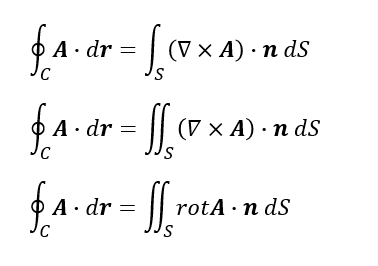
各微小面積の回転全部足したやつは、境界の回転(境界の各点におけるFの微小接線ベクトル方向への寄与全部足したやつ)に等しい。
左辺は境界におけるFの射影の大きさ(||F||cosθ)*微小ベクトルの全部足したやつとなる。微小ベクトルは単位ベクトルではないので、出力は単純な射影ベクトルの総和とはならない。
ベクトルと微分
スカラー場をベクトルで微分(勾配)
あるベクトル$${\bm x=(x_1,x_2,…,x_n)}$$がある時、
微分すべき関数$${f(\bm x)}$$は、ベクトルを入力とし、スカラーを出力とする。
微分すると出力はベクトル
これはスカラー場の勾配をとることと同じである。
その場合、$${\bm x}$$のとりうるある一点$${\bm c}$$における勾配を求めることになる。
$$
\nabla f = \frac{\partial f}{\partial \bm x}=(\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2},…,\frac{\partial f}{\partial x_n})
$$
あるいは
$$
Df(\bm x)=(D_1f(\bm x),…,D_mf(\bm x))
$$
スカラー場をベクトルで高階微分(ヘッセ行列)
p347
統計のための行列代数 上 単行本(ソフトカバー) – 2012/4/5
D. A. ハーヴィル (著)
$$
H(f)_{ij}(\bm x)=\nabla_i\nabla_jf(\bm x)=\frac{\partial^2}{\partial x_i \partial x_j}f(\bm x)
$$
$$
H(f)
=\begin{bmatrix}
\frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_1 \partial x_n}\\
\frac{\partial^2 f}{\partial x_2 \partial x_1} & \frac{\partial^2 f}{\partial x_2^2} & \cdots & \frac{\partial^2 f}{\partial x_2\partial x_n}\\
\vdots &\vdots & \ddots & \vdots\\
\frac{\partial^2 f}{\partial x_n \partial x_1} & \frac{\partial^2 f}{\partial x_n\partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_n^2}\\
\end{bmatrix}
$$
ベクトル場をスカラーで微分
勾配がヤコビ行列の行なら
こちらはヤコビ行列の列
$${\bm y(x) = (y_1(x), y_2(x), …, y_m(x))=y_1(x)\bm e_1+y_2(x)\bm e_2+…+y_m(x)\bm e_m}$$
$$
\frac{\partial \bm y}{\partial x}
=\begin{bmatrix}
\frac{\partial y_1}{\partial x} & \frac{\partial y_2}{\partial x} & \cdots & \frac{\partial y_m}{\partial x}\\
\end{bmatrix}
$$
ベクトル場をベクトルで微分(ヤコビ行列)
$${\bm y = (y_1, y_2, …, y_m)}$$
$${\bm x = (x_1, x_2, …, x_n)}$$
これをヤコビ行列という。
m=1の時、勾配の転置に一致。
p470
スタンフォード ベクトル・行列からはじめる最適化数学 (KS情報科学専門書) 単行本(ソフトカバー) – ビッグブック, 2021/3/1
ステファン・ボイド (著), リーヴェン・ヴァンデンベルグ (著), 玉木 徹 (翻訳)
$$
\frac{\partial \bm y}{\partial \bm x}
=\begin{bmatrix}
\frac{\partial y_1}{\partial x_1} & \frac{\partial y_1}{\partial x_2} & \cdots & \frac{\partial y_1}{\partial x_n}\\
\frac{\partial y_2}{\partial x_1} & \frac{\partial y_2}{\partial x_2} & \cdots & \frac{\partial y_2}{\partial x_n}\\
\vdots &\vdots & \ddots & \vdots\\
\frac{\partial y_m}{\partial x_1} & \frac{\partial y_m}{\partial x_2} & \cdots & \frac{\partial y_m}{\partial x_n}\\
\end{bmatrix}
$$
この記事が気に入ったらサポートをしてみませんか?
