増刊1：標準数

≣ はじめに

仕事柄、因子・水準についての質問をよく受けます。GUIでは因子と水準が見えますので、
　・チェックボックスは、因子：ラベル名、水準：OFFとON
　・ラジオボックスやメニューの水準は選択肢（用紙サイズならA4, B4, B5, A3, ...)
と説明しやすく、せいぜい「車両保険の車種のメニューが60個もあるのですが、どうしましょうか？」といった「水準の選択方法」の質問が来る程度です。47都道府県とか、196か国とか、、、。この時に、「同値分割をして代表値を選んでそれに水準を絞っても良いのか？」というテーマも興味深いのですが、それは今回のテーマではありません。

今回のテーマは、もう一つの質問パターンについてです。それはアナログ値についての質問です。
例えば、（公衆トイレの蛇口からでるお湯の温度を安定させるための装置のテストにおいて）「お湯の温度についての水準は、何度と何度を選ぶべきですか？」とか「CTの患者の身長についての水準を5つのパターンでテストしたいのですが、何cmと何cmと何cmと何cmと何cmを選ぶべきですか？」というものです。
そこで本エントリーではこれらの質問に答えるテクニックをご紹介します。ソフトウェア技術者にはなじみが薄いかもしれない「標準数」についてです。

≣ 標準数が生まれた経緯

19世紀後半（1877～1879年頃）に、シャルル・ルナール（Charles Renard 、1847年12月23日 - 1905年4月5日）というフランスの軍人が、「気球用のロープの太さが425種類もあって大変なのでなんとかしてくれ」という依頼を受けました。ルナールは知恵を絞り、結果として、425種類のロープを17種類まで減らすことができたのですが、それが標準数のはじまりです。（この功績から、今でも、「標準数」は「ルナール数」とも呼ばれます）

まず、ロープの太さが425種類もあったということに驚きですよね。
0.1mm刻みで1mm～50mm（5㎝）あたりまで、1.0, 1.1, 1.2, ... , 49.8, 49.9, 50.0mmのロープが存在していたということでしょうか（これで490種類となります。425種類ということは、1㎜～43.5㎜でしょうか？？）。
冷静に考えてみれば、「1.0, 1.1, 1.2の太さの違い」には意味がありそうだけれど、「49.8, 49.9, 50.0の太さの違い」にはあまり意味がなさそうに思います。（太いロープにおける0.1㎜の差は、強度にそれほど変化がないのではないかと思います。）

ルナールのアイデアも基本的には同じものでした。
次の項で述べる方法を使って、「1.0, 1.3, 1.6, 2.1, 2.7, 3.4, 4.3, 5.5, 7.1, 9.0, 11.5, 14.7, 18.8, 24.0, 30.7, 39.2, 50.0」の17種類としたのではないかと思います。（ロープが細いうちは刻みを細かく、徐々に刻みを粗くする方法）
さらに推測すると、ロープの太さは覚えやすく使いやすいものに丸める方が便利なので、「1, 1.2, 1.5, 2, 2.5, 3.5, 4.5, 5.5, 7, 9, 12, 15, 20, 24, 30, 40, 50」あたりとしたのかなと思います。（実際にルナールが使った値の情報は見つかりませんでした）
なお、この考えから標準的な数値をどう決めるかについて、ISO（ISO 3-1973）やJIS（JIS Z 8601）で標準化されました。それを「標準数」と呼びます。

身近な例でいえば、カメラの絞り（F値）が1, 1.4, 2, 2.8, 4, 5.6, 8, 11, 16, 22, 32, 45と、一見すると不規則な増加をしているように見えるのもこの関係です。（√2の等比数列をまるめたものです。）

≣ 標準数の作り方

標準数の作り方は等比数列を使うだけです。
「等比数列」という単語ですが、遠い昔に「等差数列」という単語とともに、うっすら聞いた記憶があると思います。「等差数列と等比数列」という用語は中学の数学で習うのですが、これらの数字の並びの途中を隠して答えさせる

問題：　次の［　　］に数値を書きなさい。

　2, 4, 6, 8, 10, 12, [　　], 16, 18, 20
　1, 2, 4, 8, 16, [　　], 64, 128, 256

というような問題が中学の入試に出題されるくらいですので、基本的な概念です。

では、具体的に確認していきましょう。

等差数列の例：　1, 4, 7, 10, 13, 16, 19, 22, ...
等比数列の例：　1, 3, 9, 27, 81, 243, 729, 2187, ...

上の例でいえば、等差数列の場合は「前の数に3を足す」という規則ですし、等比数列のほうは「前の数に3を掛ける」という規則となっていることを確認できます。等比数列の場合に、数が小さなうちはゆっくりと値が増えて、数が大きくなるとグンと値が増えるイメージが湧きましたでしょうか。イメージが湧かない場合は次のようなグラフを想像すると良いですよ。

3でなく、1.5なら、

等差数列の例：　1, 2.5, 4, 5.5, 7, 8.5, 10, 11.5, ...
等比数列の例：　1, 1.5, 2.3, 3.4, 5.1, 7.6, 11.4, 17.1, ...

です。

今回使用する等比数列について、「理系ラボ」に分かりやすい図がありましたので掲載します。

a(n) = a(1)×r^(n-1)

です。この式で「r」のことを「公比」と呼びます。例えば、1から始まる（a(1) = 1）、公比3の等比数列の4番目の値を知りたければ、この式に代入して、

a(4) = 1×3^(4-1)　=　27

と求められます。

水準を決めたいときには、水準数kと、最大値Nが分かっていますので、そこから公比rを求めればよいので、

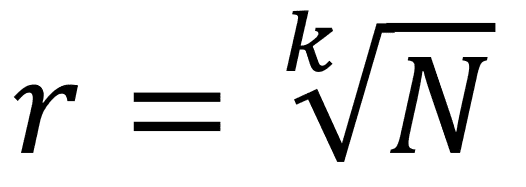
という式になります。ルート記号があって難解そうに見えますが、k乗したらNになる値を求めているだけです。

いまなら関数電卓やExcelがありますので簡単に求められます（ひょっとしたらスマートスピーカーに話しかけたら計算結果を教えてくれるかもしれません）が、この標準が決まった1973年当時は関数電卓が生まれたころで、いまのように簡単にはk乗根を計算することができませんでした。

そこで、

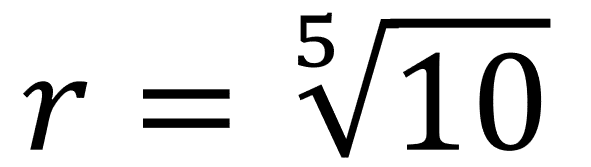
を使って、1から10までのなかで5つ取る場合の交比（1.584893192
）を計算し、そこから、{1, 1.6, 2.5, 4, 6.3}と実用的に丸めた値を標準化しました。（上述のISO 3やJIS Z 8601）

丁寧に書きますね。この時のrは10^(1/5)ですので、1.584893192です。
1.584893192×1.584893192×1.584893192×1.584893192×1.584893192＝10
なのは定義通りのことです。
あとは、初期値a(1)が1ですから、a(2)はa(1)×rで、1.584893192、
a(3)は、1.584893192×1.584893192＝2.51188643。
a(4)は、1.584893192×1.584893192×1.584893192＝3.981071702。
a(5)は、1.584893192×1.584893192×1.584893192×1.584893192＝6.309573437。
というわけです。あとは、こんなに桁はいらないので、{1, 1.6, 2.5, 4, 6.3}にしておこう、、、と、そうやって作られたのが標準数表です。
なお、標準化時はデータの個数は5だけではなく、10, 20, 40, 80も一覧表にしました。標準数の表については、JIS Z 8601やWikipediaに載っています。（仕事で使うときには、kとNを自由に決めたいので、JIS Z 8601の表ではなく、自分でExcelで作るほうが早くて便利です）

上記、{1, 1.6, 2.5, 4, 6.3}の使い方としては、例えば、100歳までの年齢から５つをサンプリングしたいときに、各値を10倍して、{10, 16, 25, 40, 63}とするなどです。サンプリング数が10個必要な時には、R10の列にある{1.00, 1.25, 1.60, ... , 6.30, 8.00}を使います。最上位桁が 1 や 2 である数が多く、8 や 9 の数が少ない点に不安を持った人は「ベンフォードの法則」が参考になります。

ということで、これを使えば簡単にアナログ値の水準を好きな個数で求めることができます。

≣ 標準数の使用上の注意点

システムの方で使いやすい（人間の感覚に合うように）値を調整している場合があります。例えば、音量を数値で指定するUIで、小さな音は細かく、大きな音は粗く番号が振られていることがあります。

このようなときには標準数を使う必要がありませんし、使ってはいけません。水準の値が持つ性質を良く調べてから使うようにしましょう。

≣ まとめ

アナログ値が整理されていない状況で多数存在するときに、この標準数が使えないか確認します。

なお、本当に等比数列で良いのか？　については物理法則までさかのぼらなければなりません。でもテストのサンプリング値の求め方と割り切って、あまり悩まないほうが良いと思います。