
Ⅸ. 変化率と微分係数・導関数【基礎微積分学:大学数学】
1. 関数の変化率
1.1. 平均変化率
さて、今回見ていくのは「関数の変化率」だ。
中学数学で、「一次関数の傾き」というものを学んだことがあると思われる。
グラフで一次関数の傾きを求める時は、
「$${x}$$が$${1}$$進んだとき$${y}$$はいくら進んだか」を探す必要があった。
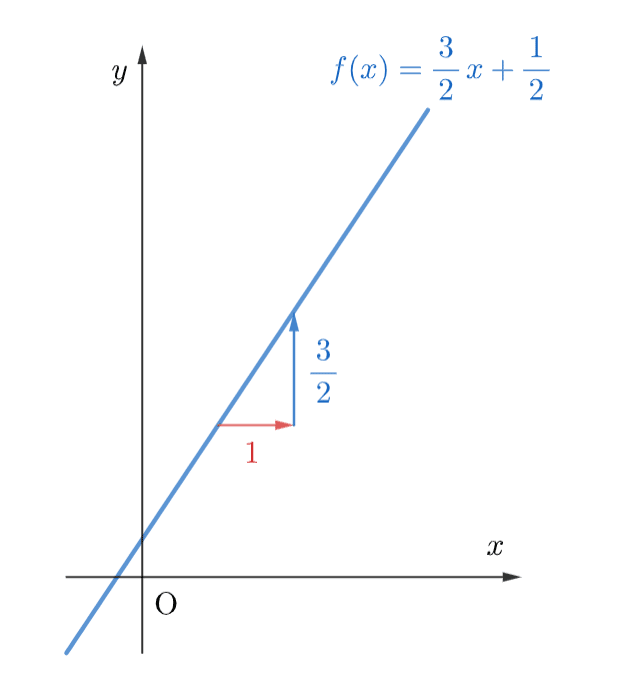
このグラフを例に説明すると$${x}$$が$${1}$$進むたび$${y}$$は$${\displaystyle\frac{\,3\,}2}$$進むので、
この関数の傾きは$${\displaystyle\frac{\,3\,}2}$$と言える。
ちなみに先程「変化率」の話から急に「傾き」の話に変わっているが、
概念で言うと(傾き)$${\subset}$$(変化率)である。
1次関数の変化率を「傾き」とも言える。
変化率も先ほど紹介した傾きの定義とあまり変わらない。
$${x}$$の変化$${1}$$に対しての$${y}$$の変化。
そして$${x}$$の変化$${1}$$に対して$${y}$$が$${c}$$変化すると
そのままの勢いで行くと$${x}$$が$${k}$$変化すると$${y}$$は$${kc}$$変化するので、
その変化率は$${\displaystyle\frac{\,kc\,}k=c}$$と言える。
ということで$${x}$$の変化を$${\mathit\Delta x}$$、$${y}$$の変化を$${\mathit\Delta y}$$だとしたら
変化率を$${\displaystyle\frac{\,\mathit\Delta y\,}{\mathit\Delta x}}$$と、何か賢っぽく表すことができる。
さて、1次関数ならどこから傾きを求めても、$${\mathit\Delta x}$$がどれだけ大きくても小さくても一定だが、
それ以外の関数はそうもいかない。こちらをご覧いただきたい。

このグラフから
・$${\text{A}}$$から$${\text{B}}$$までの変化率$${\displaystyle\frac{\,\mathit\Delta y\,}{\mathit\Delta x}\risingdotseq\frac{\,1.086\,}1=\bm{1.086}}$$
・$${\text{C}}$$から$${\text{D}}$$までの変化率$${\displaystyle\frac{\,\mathit\Delta y\,}{\mathit\Delta x}=\frac{\,-\;\!3\,}\pi=\bm{-\frac{\,3\,}{\pi}}}$$
と、位置、もしくは変化率を求める$${x}$$の変化の長さによって変化率が変わる、というのがわかる。
ということで、「どこからどこまで」を先に指定しておかなければならない。
$${[a,\;b]}$$を定義域に持ち、また$${[a,\;b]}$$で連続である関数$${f}$$に対して
$${x}$$の変化$${b-a}$$に対する$${y}$$の変化$${f(b)-f(a)}$$の比、
つまり$${\displaystyle\frac{\,f(b)-f(a)\,}{b-a}=\frac{\,\mathit\Delta y\,}{\mathit\Delta x}}$$を$${a}$$から$${b}$$までの$${f}$$の平均変化率と呼ぶ。
平均、という呼び名がついたのは、(特に曲線の関数で)
場所ごとに勢い(変化率)が違うのにそれを無視して$${a}$$から$${b}$$までの平均的な勢いを求めたからなのでは、と解釈している。
さて、これはまぁ簡単だ。……だが、次が少し面倒なことになる。
1.2. 瞬間変化率 ⇔ 微分係数
先程の平均に対して、今回は「瞬間」だ。
平均速度からの瞬間速度、となら少しピンと来る人がいるかもしれない。
測定する時間を徐々に減らしていけば、そのときどのくらいの勢いで進んでいたか、というのがわかる。
速度ではなく関数の変化率でも理屈はほとんど一緒。
ということでぐだぐだな説明は省略して、早速定義を見ていこう。
$${a}$$近方を定義域に持ち、$${a}$$近方で連続である関数$${f}$$、
また任意の実数$${h}$$に対して、
$${a}$$から$${a+h}$$までの$${f}$$の平均変化率から$${h}$$を$${0}$$への極限にかけた
$${\displaystyle\lim_{h\to0}\frac{\,f(a+h)-f(a)\,}h}$$を$${x=a}$$での$${f}$$の瞬間変化率と呼ぶ。
また、これを$${x=a}$$での$${f}$$の微分係数とも呼び、$${f'(a)}$$とも表記できる。
さて、この瞬間変化率を実際に求めてみよう。
例えば先ほどの$${g(x)=\displaystyle3\sin\frac{\,1\,}{2}x+3}$$の点$${\text{A}}$$、
つまり$${x=1}$$での瞬間変化率を求めると
(求める時に三角関数の和積公式、そして$${\displaystyle\lim_{x\to0}\frac{\,\sin x\,}x=1}$$を使う。)
$${\displaystyle g'(1)=\lim_{h\to0}\frac{\,g(1+h)-g(1)\,}{h}}$$
$${\displaystyle=\lim_{h\to0}\frac{\,\{3\sin \,(0.5+0.5h)+3\}-\{3\sin0.5-3\}\,}{h}}$$
$${\displaystyle=3\lim_{h\to0}\frac{\,\sin\,(0.5+0.5h)+\sin0.5\,}{h}\;\;\left(\longrightarrow \frac{\,0\,}0\right)}$$
$${\displaystyle=3\lim_{h\to0}\frac{\,2\cos(0.5+0.25h)\sin0.25h\,}{h}}$$
$${=\displaystyle\frac{\,3\,}2\cos\frac{\,1\,}2\lim_{h\to0}\frac{\,\sin0.25h\,}{0.25h}}$$
$${=\displaystyle\frac{\,3\,}2\cos\frac{\,1\,}2}$$
ここで、点$${\text{A}}$$からこの$${\displaystyle g'(1)=\frac{\,3\,}2\cos\frac{\,1\,}2}$$を傾きとして持つ直線を引くと、
ちょうどその点での接線になる。

そのとき丁度の勢いだけを抽出して直線にしたものだから、
($${1}$$近方では)他に触れるものがないんだね。
そして、片側極限を生かしてこれらも定義しておこう。
微分係数の条件そのまま定義での極限を片側極限に切り替えた
・$${\displaystyle\lim_{h\to0^+}\frac{\,f(a+h)-f(a)\,}h}$$を右微分係数、
・$${\displaystyle\lim_{h\to0^-}\frac{\,f(a+h)-f(a)\,}h}$$を左微分係数と呼ぶ。
YKは右微分係数を$${f'(a^+)}$$もしくは$${f'_+(a)}$$、
左微分係数を$${f'(a^-)}$$もしくは$${f'_-(a)}$$と書く。
もちろん非公式表記なので使用の推奨はしない。
次は微分係数の$${a}$$を定義域全体に一般化したものだ。
2. 導関数(Derivative)
2.1. 微分可能
「微分可能」、というのはどちらかというと関数の「連続」みたいな条件。
名前の通り次の条件を全て満足させた状態のことを指す。
関数$${f}$$が$${x=a}$$で微分可能(非公式記号$${f(a)\!:\;\mathsf{d.able}}$$)なら$${f}$$は
・$${x=a}$$で連続である
-$${f(a)}$$が存在する
-$${\displaystyle\lim_{x\to a}f(x)}$$が存在し、$${f(a)}$$と同じである
・$${x=a}$$での微分係数$${\displaystyle f'(a)=\lim_{h\to0}\frac{\,f(a+h)-f(a)\,}h}$$が存在する
上記の条件を全てを満たす関数である。
……$${\displaystyle\frac{\,0\,}0}$$の形の極限なんてできるほうが少なくない? と思うかもしれないが、割とできる。というかできないほうが少ない。
できないものと言えば
・不連続関数は全部微分不可能(ex. $${x=z\;(z\in\mathbb{R})}$$のときの$${\lfloor x\rfloor}$$)
・$${x=0}$$での絶対値関数$${y=\lvert x\rvert}$$($${1=y'(0^+)\neq y'(0^-)=-1}$$)
ぐらいなのでは? もっとあったら教えてほしい。
そしてこれから少し拡張して、区間での微分可能も見てみよう。
関数$${f}$$が開区間$${(a,\;b)}$$で微分可能なら$${f}$$は
$${^\forall k\in(a,\;b);\;\;\bm{f'(k)}}$$、$${\bm{f'(a^+)}}$$、$${\bm{f'(b^-)}}$$
が全て存在する。
連続では閉区間だったが、微分可能では開区間だ。
連続は閉区間での定義を片側連続を使って行ったのでギリギリセーフだが、
微分可能ではそうはいかないらしい。
……何しろ、数学では微分をするときに両端を捨てる節がある。
2.2. 導関数(Derivative)&微分法(Differentiation)
「導関数」は先ほど言った通り、微分係数$${f'(a)}$$の$${a}$$を$${f}$$の定義域、正確には$${f}$$が微分可能な$${x}$$全体に拡張したものだ。
$${f(^\forall x)\!:\;\mathsf{d.able};}$$
$${\displaystyle\lim_{h\to0}\frac{\,f(x+h)-f(x)\,}{h}}$$を$${f}$$の導関数と呼び、
これを記号で$${\displaystyle\frac{\,{\rm d}f\,}{{\rm d}x}=\frac{\,{\rm d}y\,}{{\rm d}x}=\frac{\rm d}{\,{\rm d}x\,}f(x)=f'(x)}$$と表す。
また、$${f}$$の$${x=a}$$での微分係数$${f'(a)}$$は$${\displaystyle\left.\frac{\,{\rm d}f\,}{{\rm d}x}\right|_{x=a}}$$と表すこともできる。
$${f'(a)=\displaystyle\left.\frac{\,{\rm d}f\,}{{\rm d}x}\right|_{x=a}}$$に関しては式$${P(a)}$$を$${\left.P(x)\right|_{x=a}}$$と表すことができることから。
また、元の関数$${f}$$から導関数$${f'}$$を求める方法を「微分法」と呼ぶ。
そして、導関数$${f'}$$に対して元の関数$${f}$$を「原始関数」と呼んだりする。
さて、記事がこの時点でかなり長くなってしまったので、
微分法の実演や様々な関数の導関数は次の記事(Ⅹ)で扱うことにする。
質問や意見などがあればぜひコメントまで。
この記事が気に入ったらサポートをしてみませんか?
