
Ⅺ. 相関比と双曲線関数【基礎微積分学:大学数学】
前置きとして、この記事の内容は、YK自身も本でしか習得していないので、内容がかなり浅い可能性がある。ご了承願う。
そして原書の「3.8. 線形近似」はこの記事ではパスしてある。
線形近似は別のシリーズで扱いたい。
1. 相関比率
1.1. 立体図形の体積と半径/高さに関するいざこざ
よく立体図形の形をした器に空気や水を入れてその時の半径や高さなどを聞く問題が出題される。
高校のときもやったのではないだろうか。
これを今回は$${{\rm d}y/{\rm d}x}$$などを使ってやってみようと思う。
ということで、まずは振り返り。
底の面積が$${A}$$ / (底の)半径が$${r}$$ / 高さが$${h}$$である
・角柱の体積:$${Ah}$$
・角錐の体積:$${\displaystyle\frac{\,1\,}3Ah}$$
・円柱の体積:$${\pi r^2h}$$
・円錐の体積:$${\displaystyle\frac{\,1\,}3\pi r^2h}$$
・球の体積:$${\displaystyle\frac{\,4\,}3\pi r^3}$$
これは、公式とかを並べるよりとかは例題を解いてみながら感を掴んでいくのがいいと思う。ということで本に載っている例題を実際に解いていこう。
例題1. 球状の風船に空気を吹き込むとき、風船の体積は$${100\;{\rm cm^3/s}}$$の比率で増加する。直径が$${50\;{\rm cm}}$$であるとき風船の半径はどれほど早く増加するか?
吹き込み始めてから経った時間を$${t\;{\rm s}}$$、風船の体積を$${V\;{\rm cm^3}}$$、
半径を$${r\;{\rm cm}}$$として式を立ててみると$${\displaystyle\frac{\,{\rm d}V\,}{{\rm d}t}=100}$$になる。
そして私たちが求めたいのは$${\displaystyle\left.\frac{\,{\rm d}r\,}{{\rm d}t}\right|_{r=25}}$$。直径が$${50\;{\rm cm}}$$なので半径は$${25\;{\rm cm}}$$。
ならば$${\displaystyle\frac{\,{\rm d}V\,}{{\rm d}t}}$$を使って$${\displaystyle\frac{\,{\rm d}r\,}{{\rm d}t}}$$の式を導き出せば大丈夫そう。
$${\displaystyle V=\frac{\,4\,}{3}\pi r^3}$$なので$${V}$$も$${r}$$も$${t}$$に関する関数として$${V}$$を$${t}$$に対して微分する。
$${\displaystyle\frac{\,{\rm d}V\,}{{\rm d}t}=\frac{\,4\,}3\pi\cdot\frac{\rm d}{\,{\rm d}t\,}r^3=4\pi r^2\frac{{\rm d}r}{\,{\rm d}t\,}=100}$$
$${\displaystyle\therefore\;\frac{{\rm d}r}{\,{\rm d}t\,}=\frac{25}{\,\pi r^2\,}}$$、
問題の答えは$${r=25}$$を代入した$${\displaystyle\left.\frac{{\rm d}r}{\,{\rm d}t\,}\right|_{r=25}=\frac{25}{\,\pi\cdot 25^2\,}=\bm{\frac{1}{\,25\pi\,}\;({\bf cm/s})}\;\;\blacksquare}$$
例題3. 水タンクが底の半径が$${2\;{\rm m}}$$、高さが$${4\;{\rm m}}$$である円錐が逆さまになったような形をしている。もし水がタンクの中に$${2\;{\rm m^3/min}}$$の速度で満たされるのならば、水の深さが$${3\;{\rm m}}$$になる瞬間の水位の上昇比率を求めよ。
また、水を入れ始めてから経った時間を$${t\;{\rm min}}$$、
タンクの体積を$${V\;{\rm m^3}}$$、水の深さを$${h\;{\rm m}}$$とすると$${\displaystyle\frac{{\rm d}V}{{\rm d}t}=2}$$
さて、ここで$${r}$$を別に指定しなかったのは相似を使って$${h}$$に関する式に表すことができるからだ。
とりあえずこれの図を書いておこう。

$${\rm\angle AOP=\angle UTP=90^\circ}$$、$${\rm\angle P}$$は共通なので$${\rm \triangle POA\sim\triangle PTU}$$、
ならば$${2:4=r:h}$$なので$${r=0.5h}$$
ということで$${V}$$を求めよう。$${\displaystyle V=\frac{\,1\,}3\pi r^2h=\frac1{\,12\,}\pi h^3}$$
これで先ほどと同様に$${V}$$と$${h}$$を$${t}$$に対する関数と見なし、
両辺を$${t}$$に対して微分。
$${\displaystyle\frac{\,{\rm d}V\,}{{\rm d}t}=\frac1{\,4\,}\pi h^2\cdot\frac{\,{\rm d}h\,}{{\rm d}t}=2}$$
$${\therefore\;\displaystyle\frac{\,{\rm d}h\,}{{\rm d}t}=\frac{4}{\,\pi h^2\,}\cdot2=\frac{8}{\,\pi h^2\,}}$$
求めるのは$${h=3}$$のときの水位の上昇速度なので
答えは$${\displaystyle\left.\frac{\,{\rm d}h\,}{{\rm d}t}\right|_{h=3}=\bm{\frac8{\,9\pi\,}\;{\bf (m/min)}}\;\;\blacksquare}$$
1.2. 動く物体の速度と距離に関するいざこざ
今回は空気や水を満たすのではなく点や人、線などが動くときの位置とか色々に関する問題。
かなり広い範囲で囲んだので、これも例題で感を掴んで行くのがいいかもしれない。
例題2. 長さ$${5\rm \;m}$$のはしごが垂直の壁面にもたれてある。はしごの下部分は壁面から$${1\rm\;m/s}$$の比率で遠ざかっていく。はしごの下部分が壁から$${3\rm\;m}$$離れるとき、はしごの上部分はどれほど速く壁面の下に滑り落ちるか?
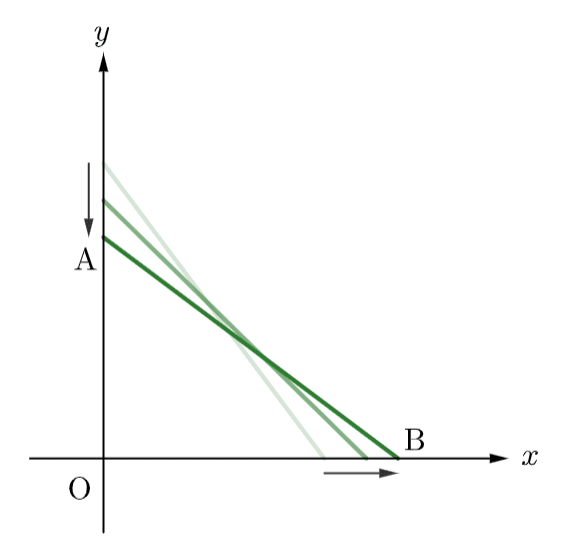
さて、変数設定。滑り始めた時点から経った時間を$${t\;\rm s}$$として、
点$${\rm A}$$、$${\rm B}$$の座標を$${(a,\;0)}$$と$${(0,\;b)}$$とすれば
$${\displaystyle\frac{\,{\rm d}b\,}{{\rm d}t}=1}$$、$${\overline{\rm AB}=5}$$から$${a=\sqrt{25-b^2}}$$。
答えとして求めたいのは$${{\rm d}a/{\rm d}t|_{b=3}}$$なので、
まずは$${{\rm d}a/{\rm d}t}$$を求める。先ほどの式の両辺を$${t}$$で微分。
$${\quad\displaystyle\frac{\,{\rm d}a\,}{{\rm d}t}}$$
$${\displaystyle=\frac{\rm d}{\,{\rm d}t\,}\sqrt{25-b^2}}$$
$${\displaystyle=\frac{\,{\rm d}b\,}{{\rm d}t}\cdot\frac{{\rm d}}{\,{\rm d}b\,}\sqrt{25-b^2}}$$
$${\displaystyle=-\frac b{\,\sqrt{25-b^2}\,}\cdot\frac{\,{\rm d}b\,}{{\rm d}t}}$$
$${\displaystyle=-\frac b{\,\sqrt{25-b^2}\,}}$$
$${b=3}$$を代入すると$${\displaystyle-\frac{3}{\,\sqrt{25-3^2}\,}=\bm{-\frac{3}{\,4\,}\;({\bf m/s})}\;\;\blacksquare}$$
過程が長いだけで思っていたより簡単だった。
これ以外の問題も、最終的に求めようとしているもの(の導関数)を知っている導関数などを使って求めればOK。
2. 双曲線関数(Hyperbolic f.)
2.1. 双曲線関数の定義
双曲線関数は文字通り二つの曲線の平均として定義される。
ということで早速定義行ってみよう。
・双曲線正弦関数$${\displaystyle\sinh x=\frac{\,e^x-e^{-x}\,}2}$$
・双曲線余弦関数$${\displaystyle\cosh x=\frac{\,e^x+e^{-x}\;}2}$$
・双曲線正接関数$${\displaystyle\tanh x=\frac{\,\sinh x\,}{\cosh x}}$$
グラフで表すとこうなる。

$${\sinh x}$$は$${e^x}$$と$${-e^{-x}}$$の平均。

$${\cosh x}$$は$${e^x}$$と$${e^{-x}}$$の平均。

$${\tanh x}$$は$${\cosh x}$$に対する$${\sinh x}$$の比。
割り算はグラフで表しても意味ないので表さなかった。
こちらは水平漸近線$${y=\pm\:1}$$が存在する。
そして三角関数同様、こちらも逆数の関数が存在する。
一応これらも双曲線関数と見なす。
・双曲線余割関数$${\displaystyle{\rm csch}\,x=\frac{1}{\,\sinh x\,}=\frac{2}{\,e^x-e^{-x}\,}}$$
・双曲線正割関数$${\displaystyle{\rm sech}\,x=\frac{1}{\,\cosh x\,}=\frac{2}{\,e^x+e^{-x}\,}}$$
・双曲線余接関数$${\displaystyle\coth x=\frac{1}{\,\tanh x\,}=\frac{\,\cosh x\,}{\sinh x}}$$
そういや、三角関数を紹介するときから関数名を和名で書いたが、
YK自身はこちらを全て英語で呼んでいる。
サイン(Sine、$${\sin}$$)、コシカント(Cosecant、$${\csc}$$)、
コサイン(Cosine、$${\cos}$$)、シカント(Secant、$${\sec}$$)、
タンジェント(Tangent、$${\tan}$$)、コタンジェント(Cotangent、$${\cot}$$)と。
$${\sinh}$$/$${\rm csch}$$などの双曲線関数も同様、「双曲(英語名)」として呼んでいる。
韓国での呼び方はこう。
2.2. 双曲線関数の性質①:方程式上の点
三角関数が単位円上の点の座標($${{\rm P}(\cos \theta,\;\sin\theta)}$$)であったように、双曲線関数もとある方程式のグラフ上の点の座標である。
そのグラフがこちら。

x軸、線分 OQ、双曲線 l に囲まれた図形の面積 S
まさに「なんだこれ」ってなるようなグラフ。
このようなグラフを扱うのはかなり先のはずなので安心してほしい。
今は点$${\rm Q}$$と色の塗られた$${S}$$の部分に焦点を合わせよう。
点$${{\rm Q}(\cosh t,\;\sinh t)}$$は$${^\forall t\in\mathbb{R}}$$に対し
常に双曲線$${x^2-y^2=1\;\;(x\geq1)}$$の上に存在する。
言い方を変えると$${\cosh^2 t-\sinh^2 t=1}$$という恒等式が$${^\forall t\in\mathbb{R}}$$に対し成立する。
証明は記事の一番下を参考願う。
そして、青色に塗られた$${x}$$軸と$${\overline{\rm OQ}}$$、そして双曲線$${l}$$に囲まれた図形の面積は、
なんと$${|\:\!t\:\!|}$$の半分ぴったりである。なぜかは……ちょっとわからない。
ちなみにこの性質は普通の三角関数も持っていて、
単位円上の点$${{\rm P}(\cos\theta,\;\sin\theta)}$$に対して中心角が$${\theta}$$である扇型の面積$${S}$$も$${|\:\!\theta\:\!|}$$の半分ぴったり。
これはラジアンでの円の面積$${S=\displaystyle\frac{1}{\,2\,}r^2\theta}$$で証明できる。

x軸、線分 OP、単位円 O に囲まれた図形の面積 S
2.3. 逆双曲線関数
こちらも逆関数が(必要なものは範囲を設定すれば)存在する。
一対一関数でないのは$${\cosh x}$$だけなので、これの定義域を$${[0,\;\infty)}$$にしてしまおう。そうしたらいける。
そして双曲線関数が指数関数を使って定義されたものなので、
その逆関数は対数関数を使って定義することができる。
・$${\sinh^{-1}x=\ln\,(x+\sqrt{x^2+1\:\!})}$$
・$${\cosh^{-1}x=\ln\,(x+\sqrt{x^2-1\:\!})}$$
・$${\tanh^{-1}x=\displaystyle\frac1{\,2\,}\ln\left(\frac{1+x}{\,1-x\,}\right)}$$
これらのグラフはこんな感じになる。



逆数双曲の逆関数はいつも通り省略。
2.4. 双曲線関数の導関数
こちらの関数の導関数も見ていこう。
何気に三角関数の導関数と似ているが、正負が違うので注意。
$${\displaystyle\frac{\rm d}{{\rm d}x}\sinh x=\cosh x\qquad\quad\frac{\rm d}{{\rm d}x}{\rm csch}\,x=-\,{\rm csch}\,x\coth x}$$
$${\displaystyle\frac{\rm d}{{\rm d}x}\cosh x=\sinh x\qquad\quad\frac{\rm d}{{\rm d}x}{\rm sech}\,x=-\,{\rm sech}\,x\tanh x}$$
$${\displaystyle\frac{\rm d}{{\rm d}x}\tanh x={\rm sech}^2\,x\qquad\quad\frac{\rm d}{{\rm d}x}\coth x=-\,{\rm csch}^2 x}$$
それぞれの正負の覚え方としては、
・三角関数は「Co-」がつくものにマイナスがついて($${\cos}$$、$${\csc}$$、$${\cot}$$)
・双曲線関数は逆数のものにだけマイナスがつく($${\rm csch}$$、$${\rm sech}$$、$${\coth}$$)
という感じ。
逆双曲線関数はこんな感じ。
$${\displaystyle\frac{\rm d}{{\rm d}x}\sinh^{-1} x=\frac{1}{\,\sqrt{1+x^2}\,}\qquad\quad\frac{\rm d}{{\rm d}x}\:\!{\rm csch}^{-1}\,x=-\,\frac{1}{\,|\:\!x\:\!|\sqrt{x^2+1}\,}}$$
$${\displaystyle\frac{\rm d}{{\rm d}x}\cosh^{-1} x=\frac{1}{\,\sqrt{x^2-1}\,}\qquad\quad\frac{\rm d}{{\rm d}x}\:\!{\rm sech}^{-1}\,x=-\,\frac{1}{\,x\sqrt{1-x^2}\,}}$$
$${\displaystyle\frac{\rm d}{{\rm d}x}\tanh^{-1} x=\frac{1}{\,1-x^2\,}\qquad\quad\frac{\rm d}{{\rm d}x}\coth^{-1} x=\frac{1}{\,1-x^2\,}}$$
これにて(YKにとっても)未知数なパートは終わり。
次は微分の応用についてやっていく。
2.5. cosh² x-sinh² x=1 の証明
$${\cosh^2 x-\sinh^2 x}$$
$${=\displaystyle\left(\frac{\,e^x+e^{-x}\,}2\right)^2-\left(\frac{\,e^x-e^{-x}\,}2\right)^2}$$
$${=\displaystyle\left(\frac{\,e^x+e^{-x}\,}2+\frac{\,e^x-e^{-x}\,}2\right)\left(\frac{\,e^x+e^{-x}\,}2-\frac{\,e^x-e^{-x}\,}2\right)}$$
$${=e^x\cdot e^{-x}=1\;\;\blacksquare}$$
この記事が気に入ったらサポートをしてみませんか?
