【熱力学４】一般化された力【つり合いの条件】

状態空間上のある一点$${(T,X)}$$とそこからすこしだけずれた点$${(T,X+dX)}$$を比較しましょう．これらの自由エネルギーの差を

$$
\begin{align*}
dF = F(T,X+dX) - F(T,X)
\end{align*}
$$

と置きます．

自由エネルギーの解析的性質

二つの状態間の自由エネルギー差は，状態をずらすのに必要になる最小の仕事ですが，それは準静的に操作をしたときの仕事であることを前回示しました．準静的な操作は，常に系を平衡に保った操作ですから，準静的な操作で移りあう状態間は滑らかに繋がっていることが期待されます．というわけで，「自由エネルギーは外部変数について連続，かつ（少なくとも片側で）微分可能である」ということがいえます．これは今は物理的に考えましたが，要請３を仮定すれば導かれます．そのことはまた後で示します．微分可能な領域では，数学的に，

$$
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\begin{align*}
dF = \sum_i \pd{F}{X_i} dX_i
\end{align*}
$$

と書くことができます．

一般化された力

準静的な操作において，系と外力について釣り合いを保ちながらある外部変数を操作しているとすれば，系に仕事をするのに必要な力は系の状態の関数とみなすことができます．このとき，温度一定のもと，微小な自由エネルギーの変化は，

$$
\begin{align*}
dF = \sum_i x_i dX_i
\end{align*}
$$

と書くことができます．このように書かれるときの力$${x_i(T,X)}$$を外部変数に共役な力と言うことにします．これは力の次元を持っていなくても構いません．なので一般化された力と言うこともあります．

特に，体積に共役な力（に負号をつけたもの）と，粒子数に共役な力は，それぞれ圧力，化学ポテンシャルと呼ばれます．

ここまでの二つの式を見比べれば，

$$
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\begin{align*}
x_i = \pd{F}{X_i}
\end{align*}
$$

ということがわかります．すなわち，外部変数に共役な力は，自由エネルギーをその外部変数で微分したものに対応しています．

つり合いの条件

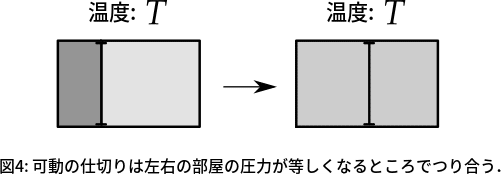
再び図２のときと似たような状況を考えてみます．図４のような状況を考えてみましょう．初め，左側の部屋の粒子の密度が高くなっていますが，仕切りが可動式の場合，仕切りに力が加わり，平衡状態では左右の部屋の圧力が等しくなっていることは経験的にわかると思います．このことを要請３［自由エネルギー極小の原理］から導きましょう．

図４で表される系の状態空間は，$${(T,V_1,V_2,N_1,N_2)}$$と書かれます．体積を$${V}$$，粒子数を$${N}$$とし，左側の部屋を系$${1}$$，右側の部屋を系$${2}$$というふうに名前を付けました．

平衡状態では自由エネルギーが極小になっているべきことから，平衡状態では自由エネルギーの変分がゼロになっています．すなわち，

$$
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\begin{align*}
dF = \pd{F}{V_1} dV_1 + \pd{F}{V_2} dV_2 =0
\end{align*}
$$

と書けます．もう少し変形すると

$$
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\begin{align*}
\pd{F}{V_1} dV_1 + \pd{F}{V_2} dV_2 &= -p_1 dV_1 - p_2 dV_2\\
&= -p_1 dV_1 + p_2 dV_1\\
&=(p_2 - p_1) dV_1\\
&=0
\end{align*}
$$

となります．ここで$${p_1,p_2}$$はそれぞれ系$${1}$$の圧力，系$${2}$$の圧力です．上式より，

$$
\begin{align*}
p_1 = p_2
\end{align*}
$$

つまり平衡状態では左右の部屋の圧力が等しくなっています．

一般に，部分系がつり合っているためには，一般化された力が等しくなっていなければならないことが示せます．

（注: 以上のことから考えてみて，化学ポテンシャルというのはなかなかに奇妙な名前に思われます．系同士が粒子をやり取りした結果，系の間で同じ値となる示強変数が化学ポテンシャルです．したがって，化学ポテンシャルは，圧力と同様に，平衡状態に向かって仕事をする力のようなものと解釈できます．普通のポテンシャルのように相対値に意味があるような量ではなくて，むしろ絶対的な値に意味がある量だと考えるべきです．ただし，連続体中に一般化された力が分布していて定常的な非平衡流れがあるとき，流れはその勾配に比例することが多いので，そういう状況では化学ポテンシャルは流れにとってのポテンシャルだといえるかもしれませんし，この場合は圧力や温度もポテンシャルらしいといえるかもしれません．）

今回のまとめ

・自由エネルギーは連続かつ片側微分可能であるとする．
・自由エネルギーの外部変数での微分によって，外部変数に共役な力が導かれる．
・部分系同士で外部変数をやり取りしあっているような場合，平衡状態では各部分系のその外部変数に共役な力が等しくなっていることが示せる．

＿＿＿＿＿＿＿＿＿＿
更新履歴

Oct. 14, 2020 化学ポテンシャルについての注釈を追加しました．
Feb.13, 2020 連続性と片側微分可能性はもともと要請にしていましたが，導かれることに気が付いたので修正しました．
Feb. 12, 2020 一般化された力が等しくなっていることがつり合うことの十分条件と解釈できる表現にうっかりなっていたので修正しました．ここで導かれたのは必要条件に過ぎません．（実際，必要十分条件なのですが，それはまた別の記事で書くつもりです．）