【流体力学ミニマル・前編】流体力学の考え方【ラグランジュの方法・オイラーの方法】
流体力学は古くは古代ギリシャのアルキメデスの浮力の原理にまで遡ることができますが,流体の運動に関して論じられるようになったのは,やはりニュートン力学の誕生後です.1700年代には粘性のない流体についてベルヌーイ,ラグランジュ,オイラーによって研究されました.1800年代には粘性のある流体についてもナビエとストークスによって研究されてきました.1930年以降はとりわけ航空力学などへの応用として流体力学は進歩してきました.応用は多岐にわたり,水道管や原子炉の配管の設計などにとどまらず,気象学,海洋学,恒星内部の運動などを論じる基礎にもなります.しかし,応用の立場から眺めなくとも,純粋な物理学としても,場の考え方の初歩としての役割や,非線形ダイナミクスの現れる例としての良い題材だと思います.
このノートでは,流体力学の基礎の基礎をまとめていきます.場とはどのような概念か,場の考え方のもとで運動や力をどう記述するかを話してから,流体の個性をどのような量を用いて記述するかを話していきます.
1.流体力学の考え方
流体とは,主として気体と液体のことを指します.これらは自由に変形できるのが特徴です.原子論の立場から考えるなら,流体は原子や分子からなる莫大だけれども有限の自由度の系です.しかし,巨視的なスケールで見れば,原子は無限に小さく,自由度は無限大と思ってもよいでしょう.このように, 流体を連続的なものとみなして運動を解析するのが流体力学の大きな特徴です.(ですから気体や液体だけでなく砂漠の砂のような流動的なものでも良いでしょう.)
低圧の気体では,気体分子運動論の領域で考えなければなりません.流体力学の結果が当てはまるのは,流れを特徴づける代表的な長さが,粒子の平均自由行程よりも十分大きければ良さそうです.気体の平均自由行程はほぼ密度に反比例し,1気圧の空気なら約60 nm です.身の回りの空気や水の流れを扱う分には,流体力学が良くあてはまるといえそうです.
(注: 代表的な長さは,考えているもののスケールを示します.たとえば水が管を流れているならその管の半径や直径をとればよい.何を代表長さにとったかを明記しさえすれば何でもよいのです.)
場とは
場(field)とは空間に分布した物理量のことです.
たとえば,流体が空間に連続に分布していると考えるなら,流体内部のある微小な部分に注目することができて,
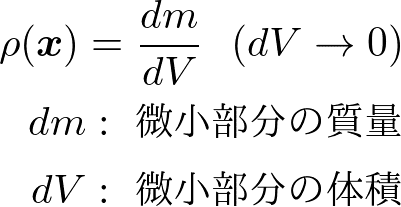
によって,ある位置における密度を定義します.これは密度の場といえます.
また,流体の各点における速度も,場所によって異なることはよくあることです.速度が空間の各点に対して定まるとき,速度場といいます.
密度の場はスカラー場の一例,速度場はベクトル場の一例となっています.流体力学では,空間的に広がった流体の内部で何が起こっているかといった細かい問題を考えたいので,場の考え方をするのが自然なのですが,そのことを次項でもう少し詳しく見ていきましょう.
流れの場
流体の運動を考えるときの一つの考え方として,流体のある部分にしるしをつけて,それにずっと注目して追いかけていくという方法が考えられます.この方法では,下図のようにある時刻である点にあった小部分が運動して,別の時刻では別の点に移っているというのを見ます.このときの小部分の座標は,時間の関数として書かれるべきものです.このような考え方をラグランジュ(Lagrange)の方法といいます.
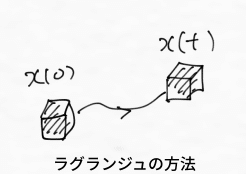
ラグランジュの方法では,変位・速度・加速度がそれぞれ
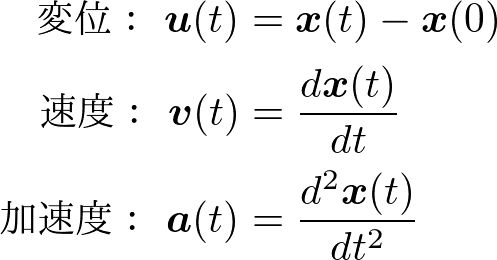
と定義されます.ただし,もちろん,
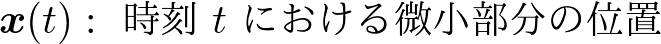
を表します.
より一般的に,ラグランジュの方法では追いかけている小部分に付随する物理量は
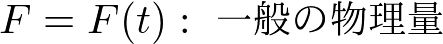
と時間の関数で書けて,その時間微分は
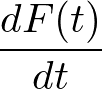
という常微分で与えられます.これを流体力学用語では物質微分(または実質微分やラグランジュ微分など)といい,ラグランジュの方法で考えているという立場を明確にするために,流体力学では
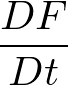
と書くことがあります.
しかし,ラグランジュの方法では小部分それぞれにしるしをつけて追いかける必要があるので,

のようにラベルするための補助変数をいれて追いかけなければなりません.(たとえば,初期位置でラベルすればOKです.)
流体力学が弾性体力学と異なるところは,その位置の変化が大きく,どこまでも流れて行ってしまうところです.そのような大きな変化を変数にとって考えると問題は手に負えなくなるので,むしろ変化量を問題にするのではなくて,「どのように流れているか」を見るために,速度の場を問題にするのが賢い方法です.このように物理では,考える問題に答えられる変数を探してから,物理法則を見つけていこうという姿勢が大切です.
というわけで,流体の運動の別の見方として,下図のように空間座標を固定しておいて,空間座標の各点を流体がどのように流れているのかを記述するという方法も考えられます.このような考え方をオイラー(Euler)の方法といいます.(おいらは場の立場,と覚えましょう.)
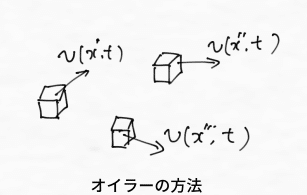
オイラーの方法では,物理量は空間座標に付随する量,つまり,場の量であり,
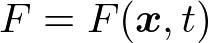
のように書けます.
オイラーの方法でも,ある小部分に注目したときの付随する物理量が時間とともにどのように変化するかを見たいときがあります.すなわち,オイラーの方法でも物質微分を考えることがあります.このときの物質微分は連鎖律より
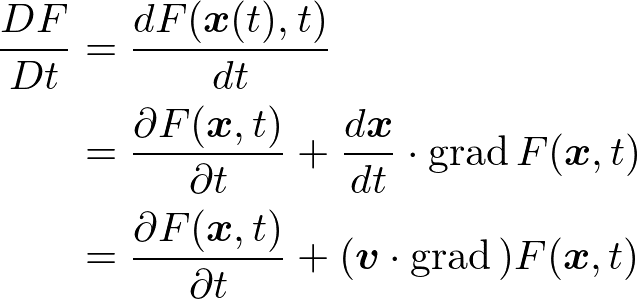
となります.
(ここで,次のように定義される記号ナブラ
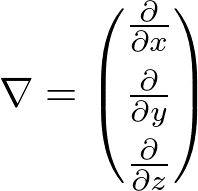
を用いると,
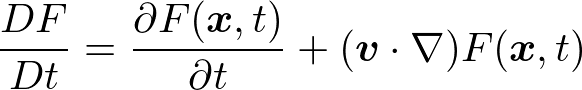
と書けます.ナブラは便利な記号ですが,どうしても顔に見えて気が散るので私はあまり使いません.かわいいのですが.)
場の考え方をしているので,単にその場所での時間での偏微分では,小部分が移動した効果が反映されません.移動したことによる物理量の変化が第二項に現れます.
オイラーの方法でも物質微分を考えるものの典型的な例として,速度・加速度があります.これらは空間のある一点に注目していても出てこないからです.
オイラーの方法では,速度・加速度がそれぞれ
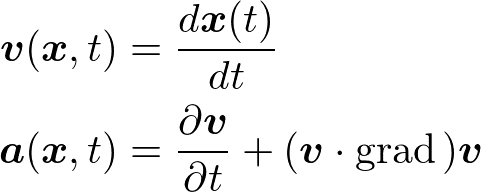
のように書けます.
加速度の第二項を行列を用いて表記すれば
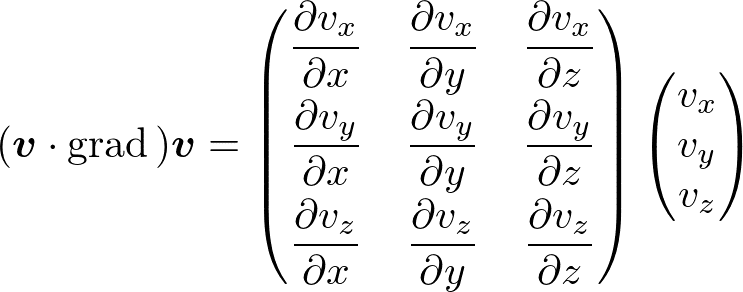
となります.この3×3行列を速度勾配テンソルといいます.テンソルがどのような概念なのかはあとで応力テンソルについて考えるときに再び触れようと思います.
加速度の第一項は局所加速度と呼ばれ,流れの時間変化による速度変化に対応します.加速度の第二項は対流加速度と呼ばれ,小部分が移動したことによる速度変化に対応します.
流体力学では,このように対流加速度の表式が非線形になっており,そのせいで解析的に解くことを非常に困難にしています.逆に言えば,この難しさのおかげで研究のし甲斐があるのだと思います.
流線,流脈線,流跡線
流れは目に見えないことが多いので,流れの中に目に見える固体粒子などを混ぜてやって,流れを可視化することがあります.このとき,得られた線が何を表すのかを判断しなくてはいけません.
流線(stream line)とは,その瞬間における速度場を滑らかにつないだものです.すなわち,流線の微小切片と速度ベクトルが平行という条件
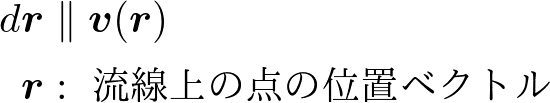
したがって,
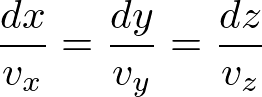
を満たすような曲線が流線です.
流跡線(path line)はある流体の小部分が実際にたどる軌跡のことです.すなわち,
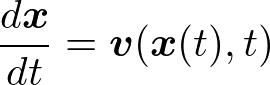
を満たすような時間をパラメータとした軌跡が流跡線です.一般に流線は時間とともに変化するので,流跡線と流線は必ずしも一致しません.
流線はオイラー的なのに対して,流跡線はラグランジュ的な概念だといえます.それゆえ流体力学では流線のほうが重要な役割を果たします.実験的に流線を知りたければ,たとえば流れの中に細かいアルミニウムの粉をまき,短い露出時間で写真をとればよく,流跡線を知りたければ,長い露出時間で写真をとればよい,となります.
最後に,流脈線(streak line)は空間のある点から出発した流体のつながりです.すなわち,流跡線がある位置を通るという条件
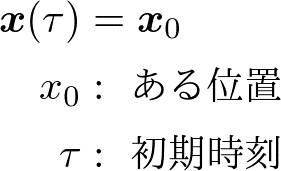
を満たすような初期時刻をパラメータとした曲線が流脈線です.
流脈線は流れの中にインキや煙を細い筋にして流してやることによって可視化できます.定常な流れでは,流線,流跡線,流脈線はどれも一致するので,流脈線から簡単に流線を求めることもできます.
流線,流跡線,流脈線の区別は,例題を解いた方がわかりやすいと思うので,次の問題を考えてみてください.
問題
二次元の速度場が
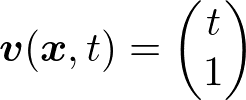
で与えられるとき,流線,流跡線,原点を出た流脈線を求めてください.
流体の変形
速度場がわかったとして,流体の実際の運動はどのようになっているのかを考えてみましょう.そのために,ある時刻である点とその近くの点を考えてみます.それらの二点は微小時間後に,それぞれ
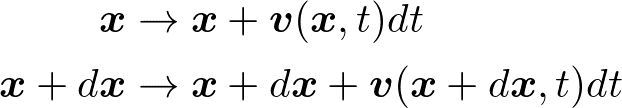
のように移動します(下図参照).
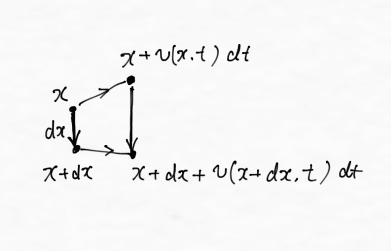
すると,微小なベクトルは
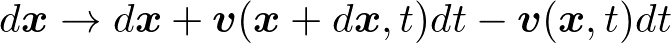
このように移り変わったことになります.
この変化分を一次まで展開すると,
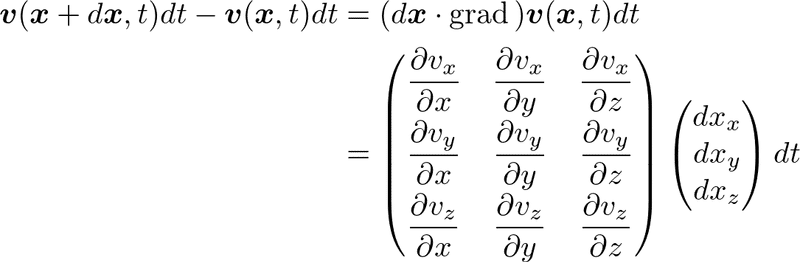
となります.したがって,速度勾配テンソルは,単位時間当たり,単位長さ当たりに微小ベクトルがどのように変形するかを記述していることがわかります.対角成分のそれぞれは,考えている座標軸方向に一致する向きに速度勾配を持つような運動になっているので,伸び縮みする運動(伸び変形)を表しているといえます.一方,非対角成分のそれぞれは,考えている座標軸方向に垂直な方向に速度勾配を持つような運動なので,積み重ねたトランプをずらすような運動を表しています.(ただし,単位時間当たり,単位長さ当たりの量なので,運動の割合を表すことに注意.)
直観として,非対角成分に現れるずらす変形は,座標軸のなす角を変える運動(こちらをせん断変形といいます)と,回転運動に分解できる気がします.それを見るためには,速度勾配テンソルを対称部分と反対称部分に分けて,
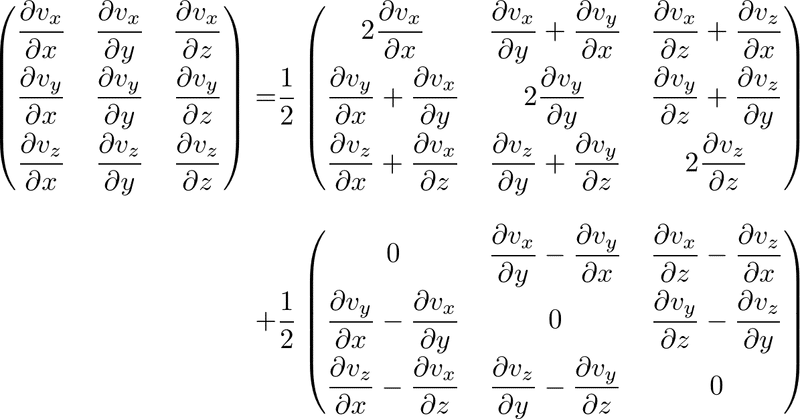
とすればよい.第一項の対称部分の非対角成分がせん断変形を表し,第二項の反対称部分は回転を表します(渦度テンソルということがあります).対称部分は伸び変形とせん断変形を合わせた運動の割合を表し,ひずみ率テンソルといいます.
今後はひずみ率テンソル,および渦度テンソルを次の記号で表すことにします.
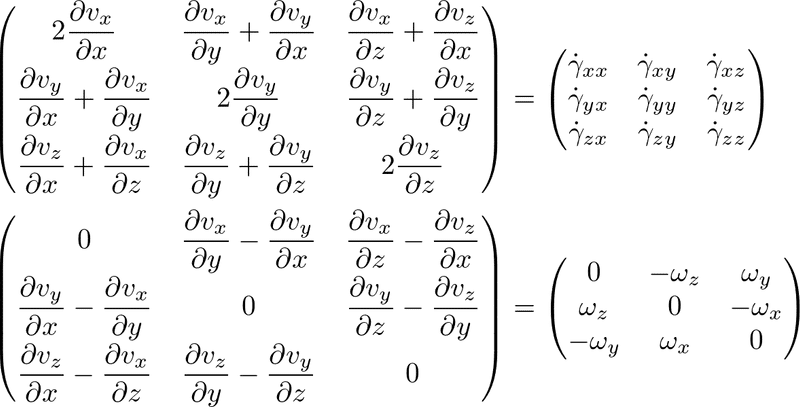
さて,今回は流体の取り扱い方として,ラグランジュの方法とオイラーの方法があることを見て,オイラーの方法のほうが流体の扱いに関しては適しているという話をしました.今のところ数学的に一般的な話をしているだけで特に物理はありません.今回で流体を扱うための「場」は整ったので,次回は物理的な仮定を取り入れて流体を記述していきましょう.
クオリティの高いノートをたくさん書けるように頑張ります!
